第72页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
10 新考法[2024长春南关区期末]一副三角尺按如图所示位置放置,OP为公共边,量角器中心与点O重合,OA为$0^{\circ }$刻度线。如果边OB与$90^{\circ }$刻度线在一条直线上,那么下列刻度线与边OC在一条直线上的是 ( )
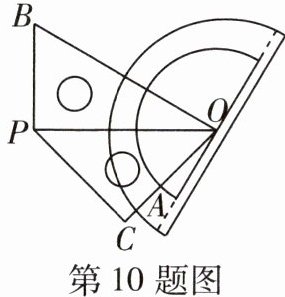
A.$15^{\circ }$刻度线
B.$30^{\circ }$刻度线
C.$45^{\circ }$刻度线
D.$75^{\circ }$刻度线

A.$15^{\circ }$刻度线
B.$30^{\circ }$刻度线
C.$45^{\circ }$刻度线
D.$75^{\circ }$刻度线
答案:
A 由题图可知∠BOP=30°,∠POC=45°,∠BOA=90°,所以∠AOC=∠BOA-∠BOP-∠POC=90°-30°-45°=15°,所以15°刻度线与边OC在一条直线上。
11 易错题如图,$∠AOB=100^{\circ },∠BOC=30^{\circ }$,小明想过点O引一条射线OD,使$∠AOD:∠BOD=1:3$($∠AOD$与$∠BOD$都小于平角),那么$∠COD$的度数是 ( )
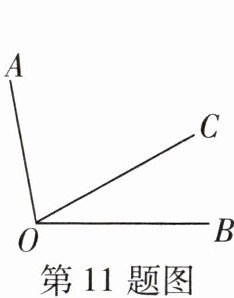
A.$45^{\circ }$
B.$45^{\circ }$或$105^{\circ }$
C.$120^{\circ }$
D.$45^{\circ }$或$120^{\circ }$

A.$45^{\circ }$
B.$45^{\circ }$或$105^{\circ }$
C.$120^{\circ }$
D.$45^{\circ }$或$120^{\circ }$
答案:
D 当OD在∠AOB的内部时,由∠AOD:∠BOD=1:3,得∠AOD=$\frac{100^\circ}{4}$=25°,所以∠COD=∠AOB-∠BOC-∠AOD=100°-30°-25°=45°;当OD在∠AOB的外部时,由∠AOD:∠BOD=1:3,得∠AOD=$\frac{100^\circ}{2}$=50°,所以∠BOD=∠AOB+∠AOD=150°,所以∠COD=∠BOD-∠BOC=150°-30°=120°。综上,∠COD的度数是45°或120°。
12 [2024渭南期末]如图,OM平分$∠AOB$,ON平分$∠AOC,∠AOB=40^{\circ },∠MON=50^{\circ }$,则$∠BOC=$____$^{\circ }$。
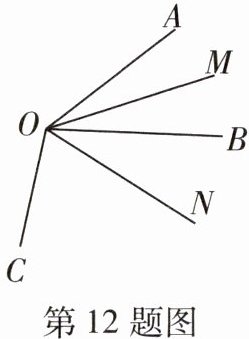

答案:
100 因为OM平分∠AOB,ON平分∠AOC,所以∠BOM=$\frac{1}{2}$∠AOB=20°,∠CON=∠AON。因为∠MON=50°,所以∠BON=∠MON-∠BOM=50°-20°=30°。因为∠AOB=40°,所以∠AON=∠CON=∠AOB+∠BON=70°,所以∠BOC=∠BON+∠CON=100°。
13 教材P127T9变式如图,OM,ON分别是$∠BOC$和$∠AOC$的平分线,$∠AOB=84^{\circ }$。
(1)$∠MON=$____;
(2)当OC在$∠AOB$内部绕点O转动时,$∠MON$的度数____改变。(填“会”或“不会”)
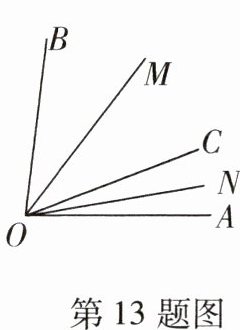
(1)$∠MON=$____;
(2)当OC在$∠AOB$内部绕点O转动时,$∠MON$的度数____改变。(填“会”或“不会”)

答案:
(1)42°;
(2)不会
(1)因为OM,ON分别是∠BOC和∠AOC的平分线,所以∠COM=$\frac{1}{2}$∠BOC,∠NOC=$\frac{1}{2}$∠AOC,又因为∠AOB=84°,所以∠MON=∠NOC+∠COM=$\frac{1}{2}$(∠AOC+∠BOC)=$\frac{1}{2}$×84°=42°。
(2)由
(1)知∠MON=$\frac{1}{2}$∠AOB=$\frac{1}{2}$×84°=42°,是定值,与OC的位置无关。
(1)42°;
(2)不会
(1)因为OM,ON分别是∠BOC和∠AOC的平分线,所以∠COM=$\frac{1}{2}$∠BOC,∠NOC=$\frac{1}{2}$∠AOC,又因为∠AOB=84°,所以∠MON=∠NOC+∠COM=$\frac{1}{2}$(∠AOC+∠BOC)=$\frac{1}{2}$×84°=42°。
(2)由
(1)知∠MON=$\frac{1}{2}$∠AOB=$\frac{1}{2}$×84°=42°,是定值,与OC的位置无关。
14 [2024黔东南州期中]如图,已知轮船A在灯塔P的北偏东$30^{\circ }$的方向上,轮船B在灯塔P的南偏东$70^{\circ }$的方向上。
(1)求从灯塔P看两轮船的视角(即$∠APB$)的度数;
(2)若轮船C在$∠APB$的平分线上,则轮船C在灯塔P的什么方向?

(1)求从灯塔P看两轮船的视角(即$∠APB$)的度数;
(2)若轮船C在$∠APB$的平分线上,则轮船C在灯塔P的什么方向?

答案:
解:
(1)由题意可知∠APN=30°,∠BPS=70°,所以∠APB=180°-∠APN-∠BPS=80°。
(2)因为PC平分∠APB,且∠APB=80°,所以∠APC=$\frac{1}{2}$∠APB=40°,所以∠NPC=∠APN+∠APC=70°,所以轮船C在灯塔P的北偏东70°的方向上。
(1)由题意可知∠APN=30°,∠BPS=70°,所以∠APB=180°-∠APN-∠BPS=80°。
(2)因为PC平分∠APB,且∠APB=80°,所以∠APC=$\frac{1}{2}$∠APB=40°,所以∠NPC=∠APN+∠APC=70°,所以轮船C在灯塔P的北偏东70°的方向上。
15 推理能力[2024天津和平区期末]
(1)如图1,将两个直角三角尺的直角顶点重合在一起。
①若$∠DCE=35^{\circ }$,则$∠ACB=$____;若$∠ACB=140^{\circ }$,则$∠DCE=$____。
②猜想$∠ACB$与$∠DCE$的数量关系,并说明理由。
(2)如图2,若两个同样的三角尺的$60^{\circ }$角的顶点重合在一起,则$∠DAB$与$∠CAE$有怎样的数量关系?请说明理由。
(3)已知$∠AOB=α,∠COD=β$(α,β都是锐角),如图3,若把它们的顶点O重合在一起,请直接写出$∠AOD$与$∠BOC$的数量关系,不必说明理由。
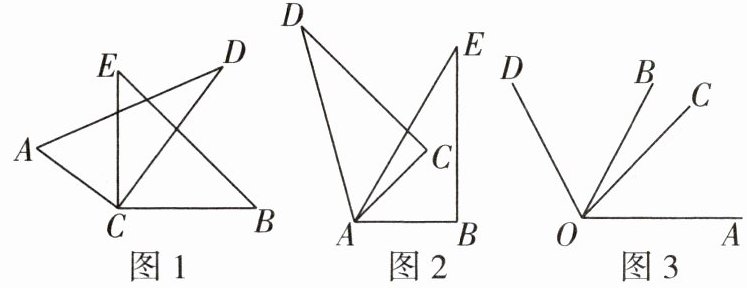
(1)如图1,将两个直角三角尺的直角顶点重合在一起。
①若$∠DCE=35^{\circ }$,则$∠ACB=$____;若$∠ACB=140^{\circ }$,则$∠DCE=$____。
②猜想$∠ACB$与$∠DCE$的数量关系,并说明理由。
(2)如图2,若两个同样的三角尺的$60^{\circ }$角的顶点重合在一起,则$∠DAB$与$∠CAE$有怎样的数量关系?请说明理由。
(3)已知$∠AOB=α,∠COD=β$(α,β都是锐角),如图3,若把它们的顶点O重合在一起,请直接写出$∠AOD$与$∠BOC$的数量关系,不必说明理由。

答案:
解:
(1)①145° 40° 因为∠ACE+∠DCE=90°=∠BCD+∠DCE,∠DCE=35°,所以∠ACB=∠ACD+∠ECB-∠DCE=90°+90°-35°=145°。若∠ACB=140°,则∠DCE=90°+90°-140°=40°。②∠ACB+∠DCE=180°。理由如下:因为∠ACB=∠ACD+∠BCD=90°+∠BCD,所以∠ACB+∠DCE=90°+∠BCD+∠DCE=90°+∠BCE=180°。
(2)∠DAB+∠CAE=120°。理由如下:因为∠DAB=∠DAC+∠CAB=60°+∠CAB,所以∠DAB+∠CAE=60°+∠CAB+∠CAE=60°+∠EAB=120°。
(3)∠AOD+∠BOC=α+β。因为∠AOD=∠AOB+∠BOD,∠BOD=∠COD-∠BOC,所以∠AOD=∠AOB+∠COD-∠BOC,即∠AOD=α+β-∠BOC,所以∠AOD+∠BOC=α+β。
(1)①145° 40° 因为∠ACE+∠DCE=90°=∠BCD+∠DCE,∠DCE=35°,所以∠ACB=∠ACD+∠ECB-∠DCE=90°+90°-35°=145°。若∠ACB=140°,则∠DCE=90°+90°-140°=40°。②∠ACB+∠DCE=180°。理由如下:因为∠ACB=∠ACD+∠BCD=90°+∠BCD,所以∠ACB+∠DCE=90°+∠BCD+∠DCE=90°+∠BCE=180°。
(2)∠DAB+∠CAE=120°。理由如下:因为∠DAB=∠DAC+∠CAB=60°+∠CAB,所以∠DAB+∠CAE=60°+∠CAB+∠CAE=60°+∠EAB=120°。
(3)∠AOD+∠BOC=α+β。因为∠AOD=∠AOB+∠BOD,∠BOD=∠COD-∠BOC,所以∠AOD=∠AOB+∠COD-∠BOC,即∠AOD=α+β-∠BOC,所以∠AOD+∠BOC=α+β。
查看更多完整答案,请扫码查看


