第19页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
1[2024长春一模]如图,数轴上表示数-1.5的点位于( )

A.AB段
B.BO段
C.OC段
D.CD段

A.AB段
B.BO段
C.OC段
D.CD段
答案:
A
2如图,已知数轴上有A,B,C,D四个点,下列说法正确的是( )

A.如果点B表示的数是10,那么点A表示的数是-20
B.如果点D表示的数是1,那么点B表示的数是0.1
C.如果点C表示的数是0.2,那么点D表示的数是$\frac{1}{2}$
D.如果点B表示的数是$\frac{1}{5}$,那么点D表示的数是$\frac{6}{5}$

A.如果点B表示的数是10,那么点A表示的数是-20
B.如果点D表示的数是1,那么点B表示的数是0.1
C.如果点C表示的数是0.2,那么点D表示的数是$\frac{1}{2}$
D.如果点B表示的数是$\frac{1}{5}$,那么点D表示的数是$\frac{6}{5}$
答案:
2 C A项,如果点B表示的数是10,那么点A表示的数是-10,说法错误;B项,如果点D表示的数是1,那么点B表示的数是0.2,说法错误;C项,如果点C表示的数是0.2,那么点D表示的数是0.5,用分数表示是$\frac{1}{2}$,说法正确;D项,如果点B表示的数是$\frac{1}{5}$,那么点D表示的数是1,说法错误。
3如图,数轴上表示有理数3的相反数的点是( )

A.M
B.N
C.P
D.Q

A.M
B.N
C.P
D.Q
答案:
3 A 3的相反数是-3,-3对应的点是点M。
4[2024洛阳洛龙区期中]数轴上,若点A和点B分别表示互为相反数的两个数,A在B的左侧,并且这两点的距离是6.4,则这两点所表示的数分别是______和______。
答案:
【解析】:
本题考查了数轴和相反数的性质。
由于点A和点B分别表示互为相反数的两个数,根据相反数的定义,这两数和为0,且它们在数轴上关于原点对称。
又因为A在B的左侧,且这两点的距离是6.4,所以A表示的数必然是负数,B表示的数必然是正数。
由于两点关于原点对称,它们到原点的距离相等,因此每点到原点的距离是6.4的一半,即3.2。
所以,A点表示的数是-3.2,B点表示的数是3.2。
【答案】:
-3.2;3.2
本题考查了数轴和相反数的性质。
由于点A和点B分别表示互为相反数的两个数,根据相反数的定义,这两数和为0,且它们在数轴上关于原点对称。
又因为A在B的左侧,且这两点的距离是6.4,所以A表示的数必然是负数,B表示的数必然是正数。
由于两点关于原点对称,它们到原点的距离相等,因此每点到原点的距离是6.4的一半,即3.2。
所以,A点表示的数是-3.2,B点表示的数是3.2。
【答案】:
-3.2;3.2
5[2024喀什期中]如图所示的数轴的单位长度为1。

请回答下列问题:
(1)如果点A,B表示的数互为相反数,那么点C表示的数是多少?
(2)如果点D,B表示的数互为相反数,那么点C,D表示的数是多少?

请回答下列问题:
(1)如果点A,B表示的数互为相反数,那么点C表示的数是多少?
(2)如果点D,B表示的数互为相反数,那么点C,D表示的数是多少?
答案:
(1)解:设点A表示的数为a,因为点A,B表示的数互为相反数,所以点B表示的数为-a。由数轴可知,点A与点B之间有6个单位长度,即-a - a = 6,解得a = -3,所以点A表示-3,点C在点A右侧2个单位长度,点C表示的数是-3 + 2 = -1。
(2)解:设点D表示的数为d,因为点D,B表示的数互为相反数,所以点B表示的数为-d。由数轴可知,点D与点B之间有9个单位长度,即-d - d = 9,解得d = -4.5,所以点D表示-4.5。点C在点D右侧5个单位长度,点C表示的数是-4.5 + 5 = 0.5。
(1)解:设点A表示的数为a,因为点A,B表示的数互为相反数,所以点B表示的数为-a。由数轴可知,点A与点B之间有6个单位长度,即-a - a = 6,解得a = -3,所以点A表示-3,点C在点A右侧2个单位长度,点C表示的数是-3 + 2 = -1。
(2)解:设点D表示的数为d,因为点D,B表示的数互为相反数,所以点B表示的数为-d。由数轴可知,点D与点B之间有9个单位长度,即-d - d = 9,解得d = -4.5,所以点D表示-4.5。点C在点D右侧5个单位长度,点C表示的数是-4.5 + 5 = 0.5。
6[2025北京五十中期中]有理数a,b,c,d在数轴上的对应点的位置如图所示,这4个数中,绝对值最大的是( )

A.a
B.b
C.c
D.d

A.a
B.b
C.c
D.d
答案:
【解析】:
本题考查的是绝对值的几何意义,即一个数在数轴上的对应点与原点的距离。
首先,观察数轴,可以看到$a$,$b$,$c$,$d$四个有理数在数轴上的位置,其中$a$的位置最靠左,距离原点最远,根据绝对值的几何意义,可以知道$a$的绝对值最大。
【答案】:A
本题考查的是绝对值的几何意义,即一个数在数轴上的对应点与原点的距离。
首先,观察数轴,可以看到$a$,$b$,$c$,$d$四个有理数在数轴上的位置,其中$a$的位置最靠左,距离原点最远,根据绝对值的几何意义,可以知道$a$的绝对值最大。
【答案】:A
7【阅读材料】
$|m - n|$的几何意义是数轴上表示数m的点与表示数n的点之间的距离。例如:$|2 - 1|$的几何意义是数轴上表示数2的点与表示数1的点之间的距离,所以$|2 - 1| = 1$。
【尝试应用】
(1)$|x + 1|$的几何意义是数轴上表示数x的点与表示数______的点之间的距离;
(2)如图,观察数轴,若$|x + 1| = 2$,则数x的值可以是______;
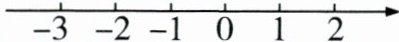
【拓展延伸】
(3)求$|x + 1| + |x - 1|$的最小值。
$|m - n|$的几何意义是数轴上表示数m的点与表示数n的点之间的距离。例如:$|2 - 1|$的几何意义是数轴上表示数2的点与表示数1的点之间的距离,所以$|2 - 1| = 1$。
【尝试应用】
(1)$|x + 1|$的几何意义是数轴上表示数x的点与表示数______的点之间的距离;
(2)如图,观察数轴,若$|x + 1| = 2$,则数x的值可以是______;
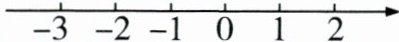
【拓展延伸】
(3)求$|x + 1| + |x - 1|$的最小值。
答案:
【解析】:
(1) 根据绝对值的几何意义,$|x + 1|$表示数轴上表示数$x$的点与表示数$-1$的点之间的距离。
(2) 对于$|x + 1| = 2$,根据绝对值的定义,可以得到两个方程:
$x + 1 = 2$ 或 $x + 1 = -2$,
解这两个方程,可以得到:
$x = 1$ 或 $x = -3$,
所以数$x$的值可以是$-3$或$1$。
(3) 对于$|x + 1| + |x - 1|$,需要考虑数轴上表示数$x$的点与表示数$-1$和$1$的点之间的距离和。
当$x$在$-1$和$1$之间时(包括$-1$和$1$),$|x + 1| + |x - 1|$表示的是数轴上表示数$x$的点与表示数$-1$和$1$的点之间的距离和,这个距离和是最小的,等于$2$。
当$x$小于$-1$或大于$1$时,$|x + 1| + |x - 1|$表示的距离和会大于$2$。
因此,$|x + 1| + |x - 1|$的最小值是$2$。
【答案】:
(1) $-1$;
(2) $-3$或$1$;
(3) $2$。
(1) 根据绝对值的几何意义,$|x + 1|$表示数轴上表示数$x$的点与表示数$-1$的点之间的距离。
(2) 对于$|x + 1| = 2$,根据绝对值的定义,可以得到两个方程:
$x + 1 = 2$ 或 $x + 1 = -2$,
解这两个方程,可以得到:
$x = 1$ 或 $x = -3$,
所以数$x$的值可以是$-3$或$1$。
(3) 对于$|x + 1| + |x - 1|$,需要考虑数轴上表示数$x$的点与表示数$-1$和$1$的点之间的距离和。
当$x$在$-1$和$1$之间时(包括$-1$和$1$),$|x + 1| + |x - 1|$表示的是数轴上表示数$x$的点与表示数$-1$和$1$的点之间的距离和,这个距离和是最小的,等于$2$。
当$x$小于$-1$或大于$1$时,$|x + 1| + |x - 1|$表示的距离和会大于$2$。
因此,$|x + 1| + |x - 1|$的最小值是$2$。
【答案】:
(1) $-1$;
(2) $-3$或$1$;
(3) $2$。
查看更多完整答案,请扫码查看


