《2025年一遍过七年级数学上册北师大版》

7 [2025 楚雄州一模]观察下列多项式:$a-2b,a^{2}-4b^{3},a^{3}-8b^{5},a^{4}-16b^{7},...$,则第n个多项式为( )

A.$a^{n}-2nb^{2n-1}$
B.$a^{n}-2^{n}b^{2n+1}$
C.$a^{n}-2^{n}b^{2n-1}$
D.$a^{n}-2^{n}b^{2n}$

答案： C

8 [2025 武汉期末]下列各方格中的四个数之间都有相同规律,根据此规律,第8个图中的$d= $( )


A.315
B.645
C.965
D.1 275

答案： B

9 如图是由同型号黑白两种颜色的正三角形瓷砖按一定规律铺设的图形。请仔细观察图形,则在第n个图中白色瓷砖比黑色瓷砖多( )


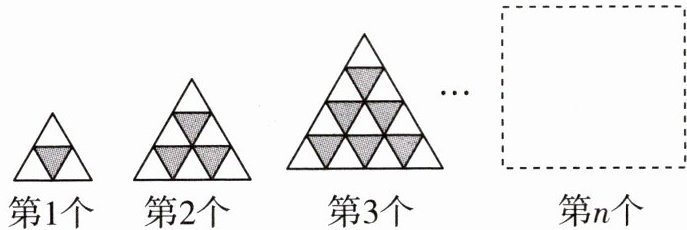
A.n块
B.2n块
C.3n块
D.$(n+1)$块

答案： D

变式 [2023 十堰中考]用火柴棍拼成如图图案,其中第①个图案由4个小等边三角形围成1个小菱形,第②个图案由6个小等边三角形围成2个小菱形……若按此规律拼下去,则第n个图案需要火柴棍的根数为____。(用含n的式子表示)

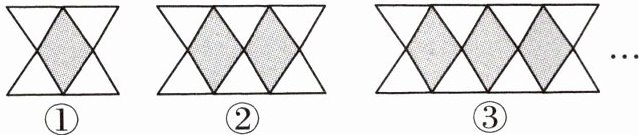
答案： 6n+6

10 [2025 大庆期中]观察下列算式,探究其规律:
$1^{2}= \frac {1×2×3}{6};1^{2}+2^{2}= \frac {2×3×5}{6};1^{2}+2^{2}+3^{2}= \frac {3×4×7}{6};1^{2}+2^{2}+3^{2}+4^{2}= \frac {4×5×9}{6};...$。
(1)根据你发现的规律,计算$1^{2}+2^{2}+3^{2}+4^{2}+5^{2}= $____。
(2)请用一个含n的代数式表示这个规律:$1^{2}+2^{2}+3^{2}+... +n^{2}= $____。

答案：
(1)55;
(2)$\frac{n×(n+1)×(2n+1)}{6}$

11 [2024 荆州期末]从2开始,连续的偶数相加,它们和的情况如表所示:
(1)若$n= 7$,则S的值为____。
(2)根据表中的规律,用含n的式子表示S的公式为$S= 2+4+6+8+... +2n= $____。
(3)根据(2)中总结的规律计算$300+302+304+... +2020+2022+2024$的值。

答案：
(1)56;
(2)n(n+1);
(3)300+302+304+…+2020+2022+2024=(2+4+6+…+2024)-(2+4+6+…+298)=1012×1013-149×150=1002806。