2025年赢在起跑线中学生快乐暑假八年级数学人教版河北少年儿童出版社
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年赢在起跑线中学生快乐暑假八年级数学人教版河北少年儿童出版社 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
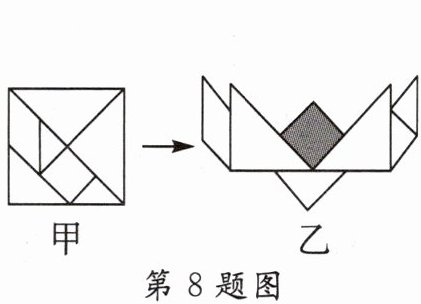
8. 如图甲,将一块正方形木板按其中的实线切成七块形状不完全相同的小木片,制成一副七巧板。用这副七巧板拼成如图乙所示的图案,则图中阴影部分的面积是整个图案面积的 ………………………………………………………………………(
A. $ \frac{1}{2\sqrt{2}} $
B. $ \frac{1}{4} $
C. $ \frac{1}{7} $
D. $ \frac{1}{8} $
D
)
A. $ \frac{1}{2\sqrt{2}} $
B. $ \frac{1}{4} $
C. $ \frac{1}{7} $
D. $ \frac{1}{8} $
答案:
D
9. 在四边形 ABCD 中,对角线 AC 与 BD 互相平分,交点为 O,在不添加任何辅助线的前提下,要使四边形 ABCD 成为矩形,还需添加一个条件,这个条件可以是
$AC = BD$ 或 $OA = OB$ 或 $ \angle ABC = 90^{\circ} $ 等(答案不唯一)
。
答案:
$AC = BD$ 或 $OA = OB$ 或 $ \angle ABC = 90^{\circ} $ 等(答案不唯一)
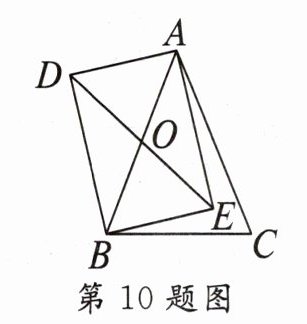
10. 如图,线段 BC 为等腰三角形 ABC 的底边,矩形 ADBE 的对角线 AB 与 DE 交于点 O,若 $ OD = 2 $,则 $ AC = $_______
4
。
答案:
4
11. 已知菱形 ABCD 的周长为 20 cm,且相邻两内角之比是 $ 1:2 $,则菱形的面积是______
$\frac{25\sqrt{3}}{2} cm^{2}$
。
答案:
$ \frac{25\sqrt{3}}{2} cm^{2} $
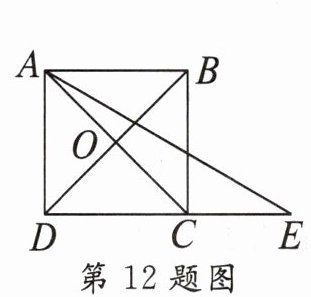
12. 如图,已知正方形 ABCD 的边长为 4,对角线 AC 与 BD 相交于点 O,点 E 在 DC 边的延长线上。若 $ \angle CAE = 15^\circ $,则 $ AE = $_______
8
。
答案:
8
13. 如图,在 $ \triangle ABC $ 中,$ AB = AC $,AD 平分 $ \angle BAC $ 交 BC 于点 D,AE 平分 $ \triangle BAC $ 的外角,且 $ \angle AEB = 90^\circ $。求证:四边形 ADBE 是矩形。
证明:
证明:
$ \because AD $ 是 $ \angle BAC $ 的平分线,$ \therefore \angle CAD = \angle BAD $.$ \because AE $ 是 $ \angle BAF $ 的平分线,$ \therefore \angle BAE = \angle EAF $.$ \because \angle CAD + \angle BAD + \angle BAE + \angle EAF = 180^{\circ} $,$ \therefore \angle BAD + \angle BAE = 90^{\circ} $,即 $ \angle DAE = 90^{\circ} $.$ \because AB = AC $,$ AD $ 平分 $ \angle BAC $,$ \therefore AD \perp BC $,即 $ \angle ADB = 90^{\circ} $.$ \because \angle AEB = 90^{\circ} $,$ \therefore \angle AEB = \angle DAE = \angle ADB = 90^{\circ} $,$ \therefore $ 四边形 $ ADBE $ 是矩形.
答案:
证明:$ \because AD $ 是 $ \angle BAC $ 的平分线,
$ \therefore \angle CAD = \angle BAD $.
$ \because AE $ 是 $ \angle BAF $ 的平分线,
$ \therefore \angle BAE = \angle EAF $.
$ \because \angle CAD + \angle BAD + \angle BAE + \angle EAF = 180^{\circ} $,
$ \therefore \angle BAD + \angle BAE = 90^{\circ} $,
即 $ \angle DAE = 90^{\circ} $.
$ \because AB = AC $,$ AD $ 平分 $ \angle BAC $,
$ \therefore AD \perp BC $,即 $ \angle ADB = 90^{\circ} $.
$ \because \angle AEB = 90^{\circ} $,$ \therefore \angle AEB = \angle DAE = \angle ADB = 90^{\circ} $,
$ \therefore $ 四边形 $ ADBE $ 是矩形.
$ \therefore \angle CAD = \angle BAD $.
$ \because AE $ 是 $ \angle BAF $ 的平分线,
$ \therefore \angle BAE = \angle EAF $.
$ \because \angle CAD + \angle BAD + \angle BAE + \angle EAF = 180^{\circ} $,
$ \therefore \angle BAD + \angle BAE = 90^{\circ} $,
即 $ \angle DAE = 90^{\circ} $.
$ \because AB = AC $,$ AD $ 平分 $ \angle BAC $,
$ \therefore AD \perp BC $,即 $ \angle ADB = 90^{\circ} $.
$ \because \angle AEB = 90^{\circ} $,$ \therefore \angle AEB = \angle DAE = \angle ADB = 90^{\circ} $,
$ \therefore $ 四边形 $ ADBE $ 是矩形.
查看更多完整答案,请扫码查看


