《2025年暑假作业兰州大学出版社七年级数学人教版》

6. 如图,汽车前照灯的反射镜具有抛物线的形状,明亮的光束是由位于抛物线反射镜焦点$F$上的光源产生的,此时光线沿着与抛物线的对称轴$AB$平行的方向射出。若$\angle FCD= 40^{\circ}$,$\angle FGH= 70^{\circ}$,则光线$FC与FG形成的\angle CFG$的度数为110°。

答案： 110°

证明：$\because \angle 1+\angle 2= 180^{\circ}$,$\therefore$AD//EF(同旁内角互补,两直线平行)。
$\therefore \angle 3= \angle D$(两直线平行,同位角相等)。
又$\because \angle 3= \angle A$,$\therefore$$\angle A= \angle D$。$\therefore AB// CD$(内错角相等,两直线平行)。
$\therefore \angle B= \angle C$(两直线平行,内错角相等)。

答案： AD//EF；两直线平行,同位角相等；∠A=∠D；内错角相等,两直线平行；两直线平行,内错角相等

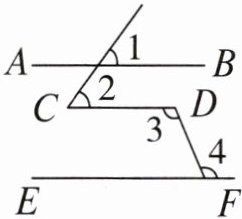
8. 如图,已知$\angle 1= \angle 2$,$\angle 3= \angle 4$。$AB与EF$有怎样的位置关系？为什么？

答案： 解:$AB// EF$,理由如下:$\because ∠1=∠2,\therefore AB// CD.$$\because ∠3=∠4,\therefore CD// EF.\therefore AB// EF.$