《2025年暑假作业兰州大学出版社七年级数学人教版》

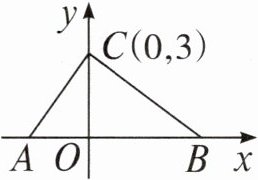
11. 如图,在平面直角坐标系中,点 $ A,B $ 的坐标分别为 $ A(a,0) $,$ B(b,0) $,且 $ a,b $ 满足 $ |a + 2| + (b - 4)^{2} = 0 $,点 $ C $ 的坐标为 $ (0,3) $。
(1) 求 $ a,b $ 的值及 $ S_{\text{三角形}ABC} $。
(2) 若点 $ M $ 在 $ x $ 轴上,且 $ S_{\text{三角形}ACM} = \frac{1}{3}S_{\text{三角形}ABC} $,试求点 $ M $ 的坐标。

答案： 解:
(1)
∵|a+2|+(b-4)²=0，
∴a+2=0,b-4=0.
∴a=-2,b=4.
∴A(-2,0),B(4,0).又
∵C(0,3),
∴AB=|-2-4|=6，CO=3.
∴S_三角形$ABC= \frac{1}{2}AB·CO=\frac{1}{2}×6×3=9.(2)$设点M的坐标为(x,0)，则AM=|x-(-2)|=|x+2|.又
∵S_三角形$ACM=\frac{1}{3}S_$三角形ABC，
∴$\frac{1}{2}AM·OC=\frac{1}{3}×9,$即$\frac{1}{2}×$|x+2|×3=3.
∴|x+2|=2,即x+2=±2，解得x=0或x=-4，故点M的坐标为(0,0)或(-4,0).

12. 数经历了从自然数到有理数,到实数,再到复数的发展过程,数学中把形如 $ a + bi $($ a,b $ 为实数)的数叫作复数,用 $ z = a + bi $ 表示,任何一个复数 $ z = a + bi $ 在平面直角坐标系中都可以用有序数对 $ Z(a,b) $ 表示。如 $ z = 1 + 2i $ 表示为 $ Z(1,2) $,则 $ z = 2 - i $ 可表示为(B)
A.$ Z(2,0) $
B.$ Z(2,-1) $
C.$ Z(2,1) $
D.$ Z(-1,2) $

答案： B

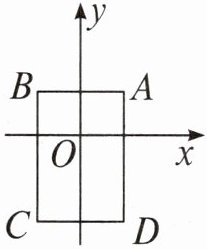
13. 如图,在平面直角坐标系中,已知点 $ A(1,1) $,$ B(-1,1) $,$ C(-1,-2) $,$ D(1,-2) $,把一根长为 2025 个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在 $ A $ 处,并按 $ A \to B \to C \to D \to A …\to $ 的规律紧绕在四边形 $ ABCD $ 的边上,则细线的另一端所在位置的点的坐标是______。

(-1,-2)

答案： 解：由点A(1,1)，B(-1,1)，C(-1,-2)，D(1,-2)，可得：
AB的长度为$|1 - (-1)| = 2$，
BC的长度为$|1 - (-2)| = 3$，
CD的长度为$|-1 - 1| = 2$，
DA的长度为$|-2 - 1| = 3$，
四边形ABCD的周长为$2 + 3 + 2 + 3 = 10$。
因为$2025 ÷ 10 = 202\cdots\cdots5$，其中余数为5。
按A→B→C→D→A的顺序，前5个单位长度的路径为：AB（2）→BC（3），此时细线另一端在点C处。
点C的坐标为(-1,-2)。
答案：(-1,-2)

14. 如图,一只甲虫在 $ 5 × 5 $ 的方格(每小格边长为 1)上沿着网格线运动,它从 $ A $ 处出发去看望 $ B,C,D $ 处的其他甲虫。规定：向上、向右走为正,向下、向左走为负。例如,从 $ A $ 到 $ B $ 记为 $ A \to B(+1,+4) $,从 $ B $ 到 $ A $ 记为 $ B \to A(-1,-4) $,其中第一个数的符号表示左右方向,第二个数的符号表示上下方向。
(1) 图中 $ B \to C $(+2,0),$ C \to $D $ (+1, $-2)。
(2) 若这只甲虫的行走路线为 $ A \to B \to C \to D $,请计算该甲虫走过的路程。
甲虫走过的路程为1+4+2+1+2=10.
(3) 若图中另有两个格点 $ M,N $,且 $ M \to A(3 - a,b - 4) $,$ M \to N(5 - a,b - 2) $,则从 $ N \to A $ 应记作什么？
因为M→A(3-a,b-4),M→N(5-a,b-2)，所以5-a-(3-a)=2，b-2-(b-4)=2，所以从点A向右走2个格点，向上走2个格点到点N，所以从N→A应记为(-2,-2).

答案： 解:
(1)因为向上向右走为正，向下向左走为负，所以图中B→C(+2,0),C→D(+1,-2).
(2)甲虫走过的路程为1+4+2+1+2=10.
(3)因为M→A(3-a,b-4),M→N(5-a,b-2)，所以5-a-(3-a)=2，b-2-(b-4)=2，所以从点A向右走2个格点，向上走2个格点到点N，所以从N→A应记为(-2,-2).