第87页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
杨辉,钱塘(今浙江杭州)人,中国南宋末年数学家、数学教育家。他编著的数学书共五种二十一卷,著有《详解九章算法》十二卷、《日用算法》两卷、《乘除通变本末》三卷、《田亩比类乘除捷法》两卷、《续古摘奇算法》两卷。其中后三种合称《杨辉算法》,朝鲜、日本等国均有译本出版,流传世界。
杨辉三角出现在杨辉编著的《详解九章算法》一书中(如下图),此书还说明表内除“1”以外的每一个数都等于()。杨辉指出,这个方法出自《释锁算书》,且我国北宋数学家贾宪大约于1050年使用过它,这表明我国发现这个三角形不晚于11世纪。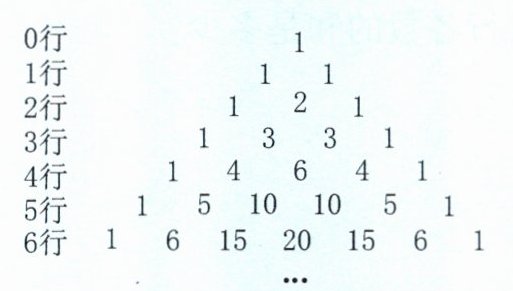
从杨辉三角中一个确定的数的“左(右)肩”出发,向右(左)上方作一条和左(右)斜边平行的射线,在这条射线上的各数的和等于这个数。我们可以得出一般性的结论:一般来说,第m条斜线上(从右上到左下)前n个数字的和,等于第()条斜线上的第()个数。
1. 根据你发现的规律,把上图三角形中第7行的数填完整。
2. 你能发现杨辉三角中的哪些数学规律?请分别用画示意图或文字描述的方法在每个杨辉三角中说明。

3. 在杨辉三角中,第10行各数的和是多少?
4. 在杨辉三角第5行中,除两端的数字1以外,行数5能被其余所有的数整除。你还能找出具有类似性质的三行吗?这时的行数p是什么数?
杨辉三角出现在杨辉编著的《详解九章算法》一书中(如下图),此书还说明表内除“1”以外的每一个数都等于()。杨辉指出,这个方法出自《释锁算书》,且我国北宋数学家贾宪大约于1050年使用过它,这表明我国发现这个三角形不晚于11世纪。

从杨辉三角中一个确定的数的“左(右)肩”出发,向右(左)上方作一条和左(右)斜边平行的射线,在这条射线上的各数的和等于这个数。我们可以得出一般性的结论:一般来说,第m条斜线上(从右上到左下)前n个数字的和,等于第()条斜线上的第()个数。
1. 根据你发现的规律,把上图三角形中第7行的数填完整。
2. 你能发现杨辉三角中的哪些数学规律?请分别用画示意图或文字描述的方法在每个杨辉三角中说明。

3. 在杨辉三角中,第10行各数的和是多少?
4. 在杨辉三角第5行中,除两端的数字1以外,行数5能被其余所有的数整除。你还能找出具有类似性质的三行吗?这时的行数p是什么数?
答案:
【解析】:根据杨辉三角的性质,表内除“1”以外的每一个数都等于它“肩上”两个数的和。对于一般性结论,通过对杨辉三角的观察和分析,第$m$条斜线上(从右上到左下)前$n$个数字的和,等于第$m + 1$条斜线上的第$n$个数。【答案】:它“肩上”两个数的和;$m + 1$;$n$。
@@答案略
@@答案略
@@3. 1024
@@4. 如 2,3,7,11 等行,行数 p 是质数
@@答案略
@@答案略
@@3. 1024
@@4. 如 2,3,7,11 等行,行数 p 是质数
查看更多完整答案,请扫码查看


