第57页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
2. 下面是小莉 5 次踢毽子的情况统计表。
|次数|第 1 次|第 2 次|第 3 次|第 4 次|第 5 次|
|数量/个|10|13|25|20|30|
根据表中的数据,在下面的统计图中,按图例画出小莉踢毽子情况的折线。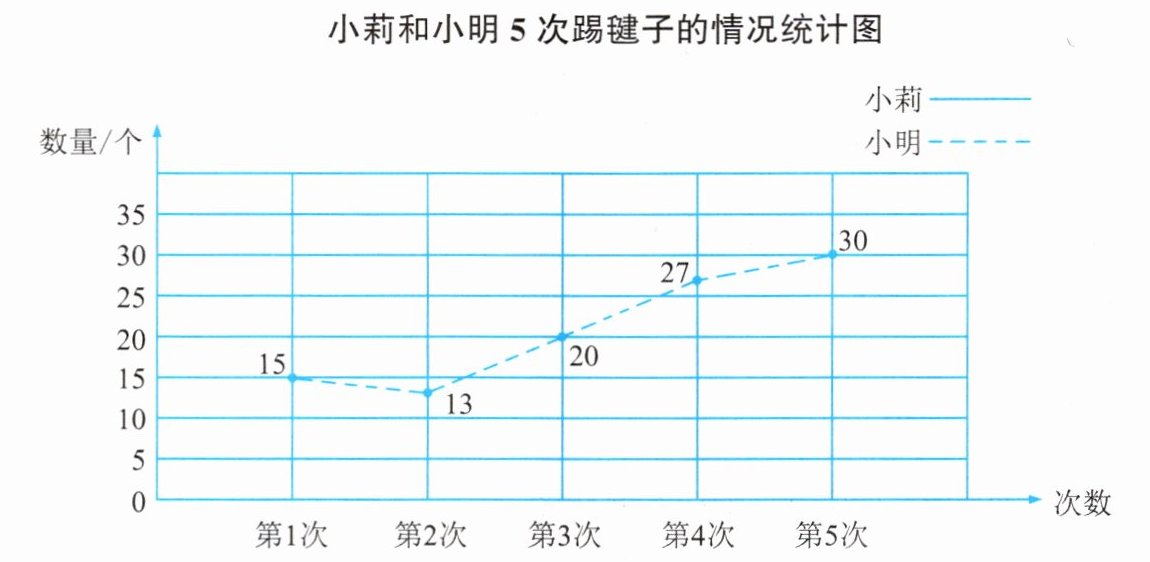
看图回答下面的问题。
(1)哪几次他们踢毽子的个数相等?
(2)从总体情况看,谁踢毽子的水平比较高?(简要说明理由)
|次数|第 1 次|第 2 次|第 3 次|第 4 次|第 5 次|
|数量/个|10|13|25|20|30|
根据表中的数据,在下面的统计图中,按图例画出小莉踢毽子情况的折线。

看图回答下面的问题。
(1)哪几次他们踢毽子的个数相等?
(2)从总体情况看,谁踢毽子的水平比较高?(简要说明理由)
答案:
【解析】:
(1)观察统计图,小莉第$2$次踢$13$个,小明第$2$次也踢$13$个;小莉第$5$次踢$30$个,小明第$5$次也踢$30$个。所以第$2$次和第$5$次他们踢毽子的个数相等。
(2)计算小莉平均每次踢毽子个数:$(10 + 13 + 25 + 20 + 30)÷5=(23 + 25 + 20 + 30)÷5=(48 + 20 + 30)÷5=(68 + 30)÷5 = 98÷5 = 19.6$(个)。
计算小明平均每次踢毽子个数:$(15 + 13 + 20 + 27 + 30)÷5=(28 + 20 + 27 + 30)÷5=(48 + 27 + 30)÷5=(75 + 30)÷5 = 105÷5 = 21$(个)。
因为$21>19.6$,小明平均每次踢毽子个数比小莉多,所以从总体情况看,小明踢毽子的水平比较高。
【答案】:
(1)第$2$次和第$5$次。
(2)小明,因为小明平均每次踢毽子个数($21$个)比小莉($19.6$个)多。
(1)观察统计图,小莉第$2$次踢$13$个,小明第$2$次也踢$13$个;小莉第$5$次踢$30$个,小明第$5$次也踢$30$个。所以第$2$次和第$5$次他们踢毽子的个数相等。
(2)计算小莉平均每次踢毽子个数:$(10 + 13 + 25 + 20 + 30)÷5=(23 + 25 + 20 + 30)÷5=(48 + 20 + 30)÷5=(68 + 30)÷5 = 98÷5 = 19.6$(个)。
计算小明平均每次踢毽子个数:$(15 + 13 + 20 + 27 + 30)÷5=(28 + 20 + 27 + 30)÷5=(48 + 27 + 30)÷5=(75 + 30)÷5 = 105÷5 = 21$(个)。
因为$21>19.6$,小明平均每次踢毽子个数比小莉多,所以从总体情况看,小明踢毽子的水平比较高。
【答案】:
(1)第$2$次和第$5$次。
(2)小明,因为小明平均每次踢毽子个数($21$个)比小莉($19.6$个)多。
查看更多完整答案,请扫码查看


