第42页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
(3)下图中的两个平行四边形完全相同,比较涂色部分的面积,()。

A. 甲>乙
B. 甲<乙
C. 甲=乙
D. 无法比较

A. 甲>乙
B. 甲<乙
C. 甲=乙
D. 无法比较
答案:
4.
(3) C
(3) C
5. 计算下面图形中涂色部分的面积。
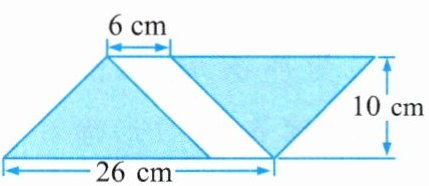
(1)
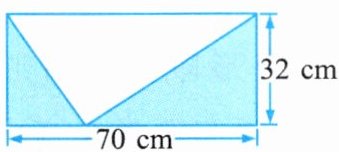
(2)
(1)


(2)
答案:
【解析】:
(1) 观察图形可知,涂色部分的面积等于底为$26$厘米、高为$10$厘米的平行四边形面积减去底为$6$厘米、高为$10$厘米的平行四边形面积。
根据平行四边形面积公式$S = 底×高$,可得:
$26×10 - 6×10=(26 - 6)×10=20×10 = 200$(平方厘米)
(2) 观察图形可知,涂色部分的面积等于长为$70$厘米、宽为$32$厘米的长方形面积减去底为$70$厘米、高为$32$厘米的三角形面积。
根据长方形面积公式$S = 长×宽$,三角形面积公式$S=\frac{1}{2}×底×高$,可得:
$70×32-\frac{1}{2}×70×32=(1 - \frac{1}{2})×70×32=\frac{1}{2}×70×32 = 1120$(平方厘米)
【答案】:
(1) $200$平方厘米
(2) $1120$平方厘米
(1) 观察图形可知,涂色部分的面积等于底为$26$厘米、高为$10$厘米的平行四边形面积减去底为$6$厘米、高为$10$厘米的平行四边形面积。
根据平行四边形面积公式$S = 底×高$,可得:
$26×10 - 6×10=(26 - 6)×10=20×10 = 200$(平方厘米)
(2) 观察图形可知,涂色部分的面积等于长为$70$厘米、宽为$32$厘米的长方形面积减去底为$70$厘米、高为$32$厘米的三角形面积。
根据长方形面积公式$S = 长×宽$,三角形面积公式$S=\frac{1}{2}×底×高$,可得:
$70×32-\frac{1}{2}×70×32=(1 - \frac{1}{2})×70×32=\frac{1}{2}×70×32 = 1120$(平方厘米)
【答案】:
(1) $200$平方厘米
(2) $1120$平方厘米
6. 爷爷打算在院子里种蔬菜,已知院子为东西长32米、南北宽21米的长方形。为了行走方便,要修筑同样宽的三条道路:道路宽2米,东西向两条,南北向一条,南北向道路垂直于东西向道路(如图中涂色部分)。余下部分种蔬菜。种蔬菜的土地面积是多少?
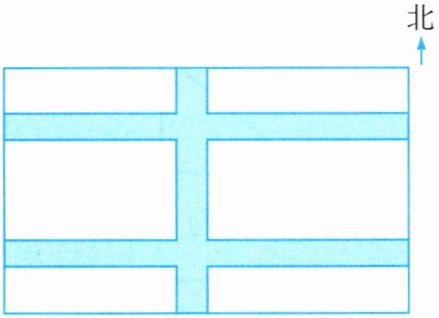

答案:
6. $(32 - 2)×(21 - 2×2)=510(m^{2})$
7. 如图1,E是长方形ABCD中的一点,求长方形的面积。先试着解答。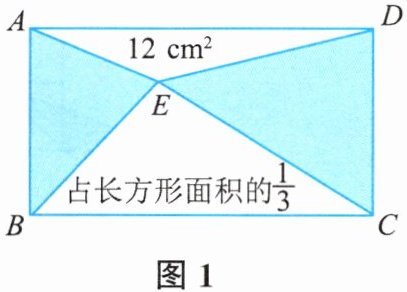
图2、图3中,涂色部分(或空白部分)面积显然占整个图形面积的$\frac{1}{2}$。

如图4,当E是长方形ABCD内的任意一点时,涂色部分面积还占$\frac{1}{2}$吗?


如图5,因为左边涂色部分面积占长方形ABFE面积的$\frac{1}{2}$,右边涂色部分面积占长方形CDEF面积的$\frac{1}{2}$,所以涂色部分面积占整个图形面积的$\frac{1}{2}$。你还能用其他方法推导吗?
相信你现在一定能解答了!
$12÷(\quad-\quad)= 72$(平方厘米)

图2、图3中,涂色部分(或空白部分)面积显然占整个图形面积的$\frac{1}{2}$。


如图4,当E是长方形ABCD内的任意一点时,涂色部分面积还占$\frac{1}{2}$吗?


如图5,因为左边涂色部分面积占长方形ABFE面积的$\frac{1}{2}$,右边涂色部分面积占长方形CDEF面积的$\frac{1}{2}$,所以涂色部分面积占整个图形面积的$\frac{1}{2}$。你还能用其他方法推导吗?
相信你现在一定能解答了!
$12÷(\quad-\quad)= 72$(平方厘米)
答案:
【解析】:根据前面的推导可知,涂色部分面积占长方形面积的$\frac{1}{2}$,空白部分中$\triangle BEC$占长方形面积的$\frac{1}{3}$,那么$12$平方厘米对应的分率就是$\frac{1}{2}-\frac{1}{3}$。
【答案】:$\boldsymbol{\frac{1}{2}}$,$\boldsymbol{\frac{1}{3}}$
【答案】:$\boldsymbol{\frac{1}{2}}$,$\boldsymbol{\frac{1}{3}}$
查看更多完整答案,请扫码查看


