《2025年轻松上初中数学升级版浙江教育出版社》

1. 有趣的三角形数。如图,从顶点起依次为第1层、第2层……仔细研究下一层与上一层点数的关系,你能发现哪些规律？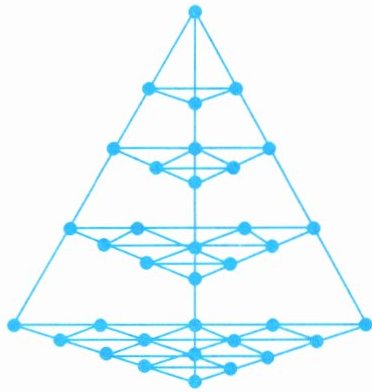
(1) 第20层有多少个点？
(2) 第15层的点与第13层的点相差多少个？
(3) 分别求出第1至3层、第1至4层、第1至5层点数的和。
分析与解：让我们进行有序的思考,根据每层数列的特点计算点的数量。

续表

问题(1)和(2)你能解决了吗？
(1) 第20层有()个点。
(2) 第15层的点与第13层的点相差()个。
求从第1层开始的几层点数的和,可将每层点数相加,也可以利用相邻的两个三角形数的和就是一个正方形数来进行计算,还可以运用下面的公式进行计算：
点的总数$=\frac{1}{6}n(n + 1)(n + 2)$(n为层数)
(3) 第1至3层点数的和是(),第1至4层点数的和是(),第1至5层点数的和是()。

答案：
(1) $\frac{(1 + 20)×20}{2}=210$
(2) $14 + 15 = 29$
(3) $10$ $20$ $35$