《2025年春如金卷课时作业AB本八年级数学上册北师大版》

18. 如图,在正方形网格中,每个小正方形的边长均为1,$\triangle ABC$的三个顶点都在格点上。
(1)直接写出$AB^{2},AC^{2},BC^{2}$的值;
(2)判断$\triangle ABC$的形状,并说明理由。

答案：

解：$(1)$由勾股定理得$ AB^{2}=AC^{2}+2^{2}=5^{2}，$$BC^{2}=3^{2}+1^{2}=10。$　　

$(2)\triangle ABC $是等腰直角三角形，理由如下：　　

因为$ AB^{2}=5，$$AC^{2}=5，$$BC^{2}=10，$　　

所以$ AB^{2}+AC^{2}=BC^{2}，$$AB = AC，$　　

因此$ \triangle ABC $是等腰直角三角形。　　

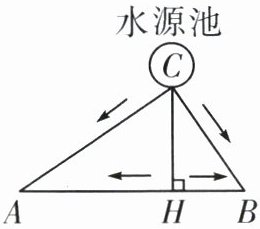
19. 如图所示,A,B两块试验田相距200 m,C为水源地,$AC=160m,BC=120m$,为了方便灌溉,现有两种方案修筑水渠。
甲方案:从水源地C直接修筑两条水渠分别到A,B;
乙方案;过点C作AB的垂线,垂足为点H,先从水源地C修筑一条水渠到AB所在直线上的H处,再从H分别向A,B进行修筑。
(1)请判断$\triangle ABC$的形状(要求写出推理过程);
(2)两种方案中,哪一种方案所修的水渠较短? 请通过计算说明。

答案： 【解析】：
(1)在$\triangle ABC$中，已知$AC = 160m$，$BC = 120m$，$AB = 200m$。
根据勾股定理的逆定理，若$a^{2}+b^{2}=c^{2}$（其中$c$为最长边），则三角形为直角三角形。
计算$AC^{2}+BC^{2}$：$160^{2}+120^{2}=25600 + 14400=40000$，而$AB^{2}=200^{2}=40000$。
所以$AC^{2}+BC^{2}=AB^{2}$，则$\triangle ABC$是直角三角形，$\angle ACB = 90^{\circ}$。
(2)甲方案所修水渠长度为$AC + BC$，$AC+BC=160 + 120=280(m)$。
因为$\triangle ABC$是直角三角形，$S_{\triangle ABC}=\frac{1}{2}AC\cdot BC=\frac{1}{2}AB\cdot CH$。
已知$AC = 160m$，$BC = 120m$，$AB = 200m$，代入$\frac{1}{2}AC\cdot BC=\frac{1}{2}AB\cdot CH$可得：
$\frac{1}{2}×160×120=\frac{1}{2}×200× CH$，
$CH=\frac{160×120}{200}=96(m)$。
在$Rt\triangle ACH$中，根据勾股定理$AH=\sqrt{AC^{2}-CH^{2}}=\sqrt{160^{2}-96^{2}}=\sqrt{(160 + 96)(160 - 96)}=\sqrt{256×64}=128(m)$。
$BH=AB - AH=200 - 128 = 72(m)$。
乙方案所修水渠长度为$CH+AH + BH=CH+AB$，$CH + AB=96+200=296(m)$。
因为$280\lt296$。
【答案】：
(1)$\triangle ABC$是直角三角形，推理过程见解析。
(2)甲方案所修的水渠较短。