《2025年春如金卷课时作业AB本八年级数学上册北师大版》

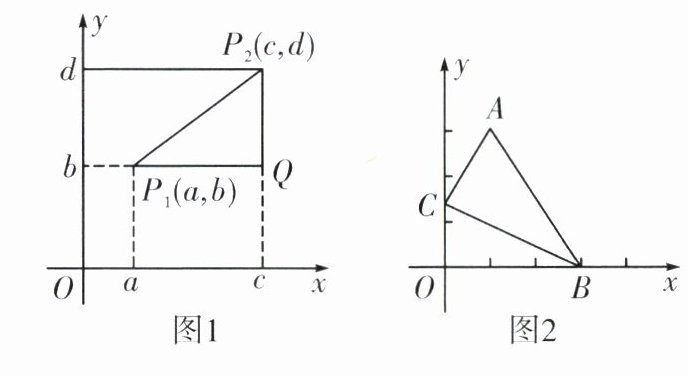
20. 小亮在网上搜索到下面的文字材料:在$x$轴上有两个点它们的坐标分别为$(a,0)$和$(c,0)$。则这两个点所成的线段的长为$|a - c|$;同样,若在$y$轴上的两点坐标分别为$(0,b)$和$(0,d)$,则这两个点所成的线段的长为$|b - d|$。如图1,在直角坐标系中的任意两点$P_1$,$P_2$,其坐标分别为$(a,b)$和$(c,d)$,分别过这两个点作两坐标轴的平行线,构成一个直角三角形,其中直角边$P_1Q = |a - c|$,$P_2Q = |b - d|$,利用勾股定理可得:线段$P_1P_2$的长为$\sqrt{(a - c)^2 + (b - d)^2}$。
根据上面材料,回答下面的问题:
(1)在平面直角坐标系中,已知$A(2,2)$,$B(6,5)$,则线段$AB$的长为______;
(2)若点$C$在$y$轴上,点$D$的坐标是$(-3,0)$,且$CD = 6$,则点$C$的坐标是______;
(3)如图2,在直角坐标系中,点$A$,$B$的坐标分别为$(1,3)$和$(3,0)$,点$C$是$y$轴上的一个动点,且$A$,$B$,$C$三点不在同一条直线上,求$\triangle ABC$周长的最小值。

答案：
解:
(1)因为$A(2,2)$,$B(6,5)$,
所以$AB=\sqrt{(6-2)^{2}+(5-2)^{2}}=\sqrt{4^{2}+3^{2}}=5$,
故答案为:5;
(2)设$C(0,m)$,
因为点D的坐标是$(-3,0)$,且$CD=6$,
所以$6^{2}=3^{2}+m^{2}$,解得$m=\pm 3\sqrt{3}$,
所以点C的坐标是:$(0,3\sqrt{3})$或$(0,-3\sqrt{3})$,
故答案为:$(0,3\sqrt{3})$或$(0,-3\sqrt{3})$;
(3)如图2,作点A关于y轴的对称点D,则点$D(-1,3)$,
所以$AC+BC+AB≥BD+AB$,当B,C,D三点共线时,$AB+AD$最小,即$△ABC$周长最小,
因为$A(1,3)$,$B(3,0)$,$D(-1,3)$,
$AB=\sqrt{(3-1)^{2}+(0-3)^{2}}=\sqrt{4+9}=\sqrt{13}$,
$DB=\sqrt{[3-(-1)]^{2}+(0-3)^{2}}=\sqrt{16+9}=5$,
所以$△ABC$周长最小值为$\sqrt{13}+5$。