《2025年春如金卷课时作业AB本八年级数学上册北师大版》

15. 解下列各题。
（1）已知$y=\sqrt{x-2025}-\sqrt{2025-x}-2021$，求$x+y$的平方根；
（2）已知$x=2-\sqrt{2024}$，求代数式$x^{3}-3x^{2}-2024x+5$的值。

答案： 解：
(1) 因为 $y = \sqrt {x - 2025} - \sqrt {2025 - x} - 2021$，所以 $x - 2025 \geq 0$，$2025 - x \geq 0$，所以 $x = 2025$，所以 $y = - 2021$，所以 $x + y = 2025 - 2021 = 4$，所以 $x + y$ 的平方根为 $\pm 2$。
(2) 因为 $x = 2 - \sqrt {2024}$，所以 $(x - 2)^{2} = 2024$，所以 $x^{3} - 3x^{2} - 2024x + 5$
$= x(x^{2} - 3x) - 2024x + 5$
$= x(x^{2} - 4x + 4 + x - 4) - 2024x + 5$
$= x(x - 2)^{2} + x^{2} - 4x - 2024x + 5$
$= 2024x + x^{2} - 4x - 2024x + 5$
$= x^{2} - 4x + 5$
$= x^{2} - 4x + 4 + 1$
$= (x - 2)^{2} + 1$
$= 2025$。

16. 已知一次函数$y=-2x-6$。
（1）画出函数的图象；
（2）求图象与$x$轴、$y$轴的交点$A,B$的坐标；
（3）求$\triangle AOB$的面积。

答案：
解：
(1) 画图如下：

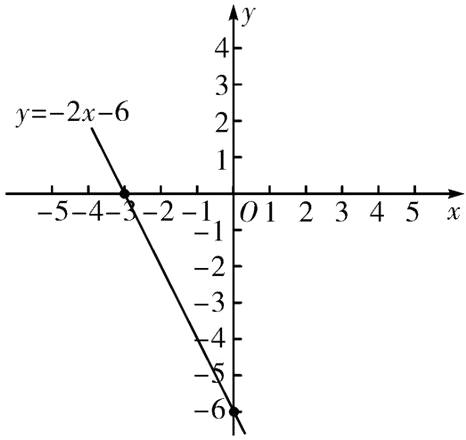
(2) 当 $x = 0$ 时，$y = - 6$；当 $y = 0$ 时，$x = - 3$，所以与 $x$ 轴的交点 $A$ 的坐标：$( - 3,0 )$；与 $y$ 轴的交点 $B$ 的坐标：$( 0, - 6 )$。
(3) $\triangle AOB$ 的面积 $= AO × BO × \frac {1}{2} = 3 × 6 × \frac {1}{2} = 9$。

17. “交通管理条例第三十五条”规定：小汽车在城市街道上行驶速度不得超过$70km/h$。如图，一辆小汽车在一条城市街道上直线行驶，某一时刻刚好行驶到距路对面的车速检测仪正前方$50m$的$B$处，过了$6s$后，测得小汽车与车速检测仪间距离为$130m$，这辆小汽车超速了吗？

答案： 解：由勾股定理得 $BC = 120 \mathrm{~m}$，$v = 120 ÷ 6 = 20 (\mathrm{m} / \mathrm{s})$，$20 \mathrm{~m} / \mathrm{s} = 72 \mathrm{~km} / \mathrm{h}$，$72 ＞ 70$，所以这辆小汽车超速了。