20. 综合与实践
【问题情境】
在平面直角坐标系中,有不重合的两点$A(x_{1},y_{1})$和$B(x_{2},y_{2})$,若$x_{1}=x_{2}$,则$AB// y$轴,且线段$AB$的长度为$|y_{1}-y_{2}|$;若$y_{1}=y_{2}$,则$AB// x$轴,且线段$AB$的长度为$|x_{1}-x_{2}|$。
【知识应用】
(1)若点$A(-1,1),B(2,1)$,则$AB// x$轴,$AB$的长度为
【拓展延伸】
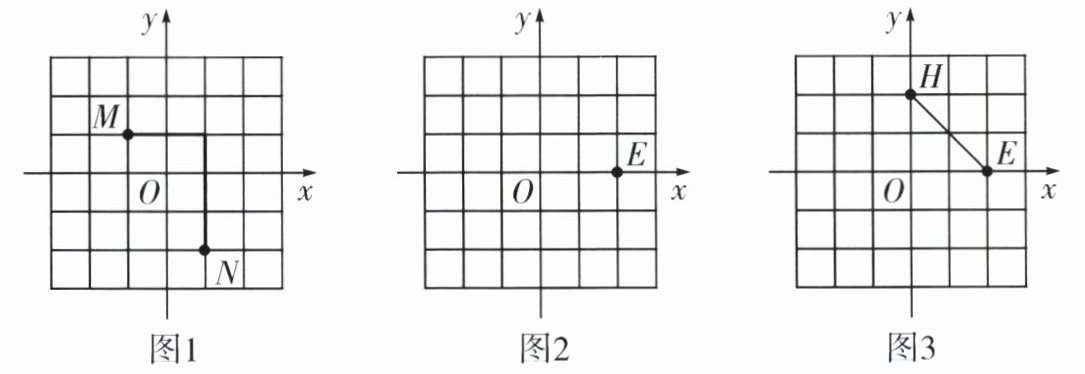
我们规定:平面直角坐标系中,任意不重合的两点$M(x_{1},y_{1}),N(x_{2},y_{2})$之间的折线距离为$d(M,N)=|x_{1}-x_{2}|+|y_{1}-y_{2}|$。例如:图1中,点$M(-1,1)$与点$N(1,-2)$之间的折线距离为$d(M,N)=|-1-1|+|1-(-2)|=2+3=5$。
【问题解决】
(2)如图2,已知$E(2,0)$,若$F(-1,-1)$,则$d(E,F)=$
(3)如图2,已知$E(2,0),G(1,t)$,若$d(E,G)=3$,则$t$的值为
(4)如图3,已知$E(2,0),H(0,2)$,点$P$是$\triangle EOH$的边上一点,若$d(E,P)=\sqrt{6}$,求点$P$的坐标。
【问题情境】
在平面直角坐标系中,有不重合的两点$A(x_{1},y_{1})$和$B(x_{2},y_{2})$,若$x_{1}=x_{2}$,则$AB// y$轴,且线段$AB$的长度为$|y_{1}-y_{2}|$;若$y_{1}=y_{2}$,则$AB// x$轴,且线段$AB$的长度为$|x_{1}-x_{2}|$。
【知识应用】
(1)若点$A(-1,1),B(2,1)$,则$AB// x$轴,$AB$的长度为
3
;【拓展延伸】
我们规定:平面直角坐标系中,任意不重合的两点$M(x_{1},y_{1}),N(x_{2},y_{2})$之间的折线距离为$d(M,N)=|x_{1}-x_{2}|+|y_{1}-y_{2}|$。例如:图1中,点$M(-1,1)$与点$N(1,-2)$之间的折线距离为$d(M,N)=|-1-1|+|1-(-2)|=2+3=5$。
【问题解决】
(2)如图2,已知$E(2,0)$,若$F(-1,-1)$,则$d(E,F)=$
4
;(3)如图2,已知$E(2,0),G(1,t)$,若$d(E,G)=3$,则$t$的值为
2 或 -2
;(4)如图3,已知$E(2,0),H(0,2)$,点$P$是$\triangle EOH$的边上一点,若$d(E,P)=\sqrt{6}$,求点$P$的坐标。

解:① 点$P$在$OE$边上,可设点$P$的坐标为$(x, 0)$,因为$d (E, P) = \sqrt {6}$。所以$| x - 2 | + 0 = \sqrt {6}$,所以$x = 2 + \sqrt {6}$,或$x = 2 - \sqrt {6}$(都不符合题意),② 点$P$在$OH$边上,可设点$P$的坐标为$(0, y)$,因为$d (E, P) = \sqrt {6}$。所以$| 2 - 0 | + | y | = \sqrt {6}$,所以$y = \sqrt {6} - 2$,所以$P (0, \sqrt {6} - 2)$,③ 点$P$在$HE$边上,可设点$P$的坐标为$(m, - m + 2)$,因为$d (E, P) = \sqrt {6}$。所以$| m - 2 | + | - m + 2 | = \sqrt {6}$,$m = 2 - \frac {\sqrt {6}}{2}$,所以$P \left(2 - \frac {\sqrt {6}}{2}, \frac {\sqrt {6}}{2} \right)$ 所以符合条件的点$P$坐标为$P (0, \sqrt {6} - 2)$,$P \left(2 - \frac {\sqrt {6}}{2}, \frac {\sqrt {6}}{2} \right)$。
答案:
解:
(1) 由题意得:$AB$ 的长度为 $| - 1 - 2 | = 3$。故答案为:3。
(2) ① $d (E, F) = | 2 - ( - 1 ) | + | 0 - ( - 1 ) | = 4$。故答案为:4。
(3) 因为 $E (2,0)$,$G (1, t)$,$d (E, G) = 3$,所以 $| 2 - 1 | + | 0 - t | = 3$,解得:$t = \pm 2$。故答案为:2 或 $- 2$。
(4) ① 点 $P$ 在 $OE$ 边上,可设点 $P$ 的坐标为 $(x, 0)$,因为 $d (E, P) = \sqrt {6}$。所以 $| x - 2 | + 0 = \sqrt {6}$,所以 $x = 2 + \sqrt {6}$,或 $x = 2 - \sqrt {6}$(都不符合题意),② 点 $P$ 在 $OH$ 边上,可设点 $P$ 的坐标为 $(0, y)$,因为 $d (E, P) = \sqrt {6}$。所以 $| 2 - 0 | + | y | = \sqrt {6}$,所以 $y = \sqrt {6} - 2$,所以 $P (0, \sqrt {6} - 2)$,③ 点 $P$ 在 $HE$ 边上,可设点 $P$ 的坐标为 $(m, - m + 2)$,因为 $d (E, P) = \sqrt {6}$。所以 $| m - 2 | + | - m + 2 | = \sqrt {6}$,$m = 2 - \frac {\sqrt {6}}{2}$,所以 $P \left(2 - \frac {\sqrt {6}}{2}, \frac {\sqrt {6}}{2} \right)$ 所以符合条件的点 $P$ 坐标为 $P (0, \sqrt {6} - 2)$,$P \left(2 - \frac {\sqrt {6}}{2}, \frac {\sqrt {6}}{2} \right)$。
(1) 由题意得:$AB$ 的长度为 $| - 1 - 2 | = 3$。故答案为:3。
(2) ① $d (E, F) = | 2 - ( - 1 ) | + | 0 - ( - 1 ) | = 4$。故答案为:4。
(3) 因为 $E (2,0)$,$G (1, t)$,$d (E, G) = 3$,所以 $| 2 - 1 | + | 0 - t | = 3$,解得:$t = \pm 2$。故答案为:2 或 $- 2$。
(4) ① 点 $P$ 在 $OE$ 边上,可设点 $P$ 的坐标为 $(x, 0)$,因为 $d (E, P) = \sqrt {6}$。所以 $| x - 2 | + 0 = \sqrt {6}$,所以 $x = 2 + \sqrt {6}$,或 $x = 2 - \sqrt {6}$(都不符合题意),② 点 $P$ 在 $OH$ 边上,可设点 $P$ 的坐标为 $(0, y)$,因为 $d (E, P) = \sqrt {6}$。所以 $| 2 - 0 | + | y | = \sqrt {6}$,所以 $y = \sqrt {6} - 2$,所以 $P (0, \sqrt {6} - 2)$,③ 点 $P$ 在 $HE$ 边上,可设点 $P$ 的坐标为 $(m, - m + 2)$,因为 $d (E, P) = \sqrt {6}$。所以 $| m - 2 | + | - m + 2 | = \sqrt {6}$,$m = 2 - \frac {\sqrt {6}}{2}$,所以 $P \left(2 - \frac {\sqrt {6}}{2}, \frac {\sqrt {6}}{2} \right)$ 所以符合条件的点 $P$ 坐标为 $P (0, \sqrt {6} - 2)$,$P \left(2 - \frac {\sqrt {6}}{2}, \frac {\sqrt {6}}{2} \right)$。
查看更多完整答案,请扫码查看


