《2025年春如金卷课时作业AB本八年级数学上册北师大版》

17. 已知一个正数的平方根是$2a-3$与$5-a,2b+4$的立方根是2。
(1)求$a,b$的值;
(2)求$a+2b$的平方根。

答案： 17.解:
(1)根据题意可知,2a−3+5−a=0,2b+4=8，解得:a=−2,b=2;
(2)因为a=−2,b=2,所以a+2b=−2+4=2,所以a+2b的平方根±$\sqrt{2}$。

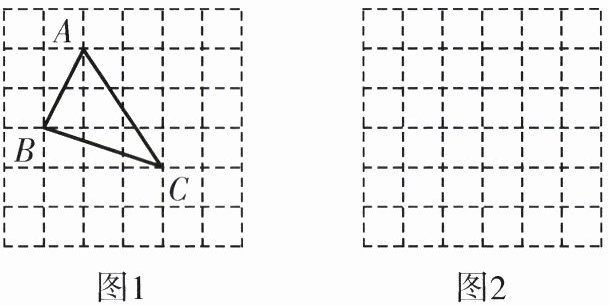
18. 如图1,是小辉同学在正方形网格中(每个小正方形的边长为1),画出的格点$\triangle ABC$($\triangle ABC$的三个顶点都在正方形的顶点处)已知$AB,BC,AC$三边的长分别为$\sqrt{5},\sqrt{10},\sqrt{13}$,请你参照小辉的方法在图2的正方形网格图中画出格点三角形$\triangle DEF$,使得$DE,EF,DF$三边的长分别为$\sqrt{2},\sqrt{8},\sqrt{10}$,然后回答下列问题。
(1)判断$\triangle DEF$的形状,说明理由。
(2)求这个三角形的面积。

答案：
18.解:如图2所示，
(1)△DEF是直角三角形，理由是:因为DE²+EF²=($\sqrt{2}$)²+($\sqrt{8}$)²=10,DF²=($\sqrt{10}$)²=10,所以DE²+EF²=DF²,所以△DEF是直角三角形;
(2)S△DEF=$\frac{1}{2}$DE·EF=$\frac{1}{2}$×$\sqrt{2}$×$\sqrt{8}$=2。