18. 根据背景素材,在两种解决方法里选择其中一种作答。
|计算遮雨棚的高度|
|----|
|背景素材|如图,15只空油桶(每只油桶底面的直径均为50cm)堆在一起,要给它们盖一个遮雨棚,遮雨棚起码要多高?($\sqrt{3}\approx 1.732,\sqrt{2}\approx 1.414$,结果精确到$0.1cm$)|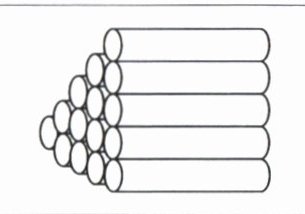
|问题解决|
|解决方法一|如图,某小组同学通过测量不同层数的高度,完成了如下的表格:|
| |油桶层数$n$|1|2|3|4|$\cdots$|
| |遮雨棚高度$y$|50cm|93.3cm|136.6cm|179.9cm|$\cdots$|
| |(1)根据表格内容,求出遮雨棚高度$y$和层数$n$的关系式;|
| |(2)当油桶层数是5层时,这样遮雨棚高度是多少?|
|解决方法二|某小组同学根据油桶的摆放方式,绘制了如下截面图,$A,B,C$三点都是对应圆的圆心,$AD\perp BC$。|
| |(1)判断$\triangle ABC$的形状,并说明理由;|
| |(2)求出遮雨棚的高度。|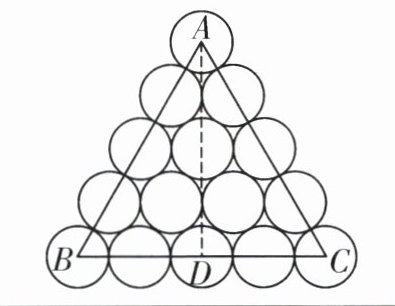
解决方法一 (1) 由表格可知:一层,遮雨棚高度为 $50 \mathrm{~cm}$,二层,遮雨棚高度为 $(50 + 43.3) \mathrm{cm}$,三层,遮雨棚高度为 $(50 + 43.3 × 2) \mathrm{cm}$,则遮雨棚高度 $y$ 和层数 $n$ 的关系式为:$y = 50 + 43.3 × (n - 1) = 43.3n + 6.7$;
(2) 当油桶层数是 5 层时,遮雨棚高度为:$43.3 × 5 + 6.7 = 223.2 (\mathrm{cm})$;
|计算遮雨棚的高度|
|----|
|背景素材|如图,15只空油桶(每只油桶底面的直径均为50cm)堆在一起,要给它们盖一个遮雨棚,遮雨棚起码要多高?($\sqrt{3}\approx 1.732,\sqrt{2}\approx 1.414$,结果精确到$0.1cm$)|

|问题解决|
|解决方法一|如图,某小组同学通过测量不同层数的高度,完成了如下的表格:|
| |油桶层数$n$|1|2|3|4|$\cdots$|
| |遮雨棚高度$y$|50cm|93.3cm|136.6cm|179.9cm|$\cdots$|
| |(1)根据表格内容,求出遮雨棚高度$y$和层数$n$的关系式;|
| |(2)当油桶层数是5层时,这样遮雨棚高度是多少?|

|解决方法二|某小组同学根据油桶的摆放方式,绘制了如下截面图,$A,B,C$三点都是对应圆的圆心,$AD\perp BC$。|
| |(1)判断$\triangle ABC$的形状,并说明理由;|
| |(2)求出遮雨棚的高度。|

解决方法一 (1) 由表格可知:一层,遮雨棚高度为 $50 \mathrm{~cm}$,二层,遮雨棚高度为 $(50 + 43.3) \mathrm{cm}$,三层,遮雨棚高度为 $(50 + 43.3 × 2) \mathrm{cm}$,则遮雨棚高度 $y$ 和层数 $n$ 的关系式为:$y = 50 + 43.3 × (n - 1) = 43.3n + 6.7$;
(2) 当油桶层数是 5 层时,遮雨棚高度为:$43.3 × 5 + 6.7 = 223.2 (\mathrm{cm})$;
答案:
解:解决方法一
(1) 由表格可知:一层,遮雨棚高度为 $50 \mathrm{~cm}$,二层,遮雨棚高度为 $(50 + 43.3) \mathrm{cm}$,三层,遮雨棚高度为 $(50 + 43.3 × 2) \mathrm{cm}$,则遮雨棚高度 $y$ 和层数 $n$ 的关系式为:$y = 50 + 43.3 × (n - 1) = 43.3n + 6.7$;
(2) 当油桶层数是 5 层时,遮雨棚高度为:$43.3 × 5 + 6.7 = 223.2 (\mathrm{cm})$;
解决方法二
(1) $\triangle ABC$ 为等边三角形,理由如下:因为 $AB = 4 × 50 = 200 \mathrm{~cm}$,$BC = 4 × 50 = 200 \mathrm{~cm}$,$AC = 4 × 50 = 200 \mathrm{~cm}$,所以 $AB = AC = BC$,所以 $\triangle ABC$ 为等边三角形;
(2) 因为 $AD \perp BC$ 于 $D$,$\triangle ABC$ 为等边三角形,所以 $\angle ADB = 90^{\circ}$,$BD = \frac {1}{2}BC = 100$,在 $\mathrm{Rt} \triangle ABD$ 中,$AB^{2} = BD^{2} + AD^{2}$,所以 $AD = \sqrt {AB^{2} - BD^{2}} = \sqrt {200^{2} - 100^{2}} = 100 \sqrt {3}$,所以油桶的最高点到地面的距离 $= 25 + 100 \sqrt {3} + 25 = 50 + 100 \sqrt {3} \approx 223.2 (\mathrm{cm})$。答:遮雨棚的高度约为 $223.2 \mathrm{~cm}$。
(1) 由表格可知:一层,遮雨棚高度为 $50 \mathrm{~cm}$,二层,遮雨棚高度为 $(50 + 43.3) \mathrm{cm}$,三层,遮雨棚高度为 $(50 + 43.3 × 2) \mathrm{cm}$,则遮雨棚高度 $y$ 和层数 $n$ 的关系式为:$y = 50 + 43.3 × (n - 1) = 43.3n + 6.7$;
(2) 当油桶层数是 5 层时,遮雨棚高度为:$43.3 × 5 + 6.7 = 223.2 (\mathrm{cm})$;
解决方法二
(1) $\triangle ABC$ 为等边三角形,理由如下:因为 $AB = 4 × 50 = 200 \mathrm{~cm}$,$BC = 4 × 50 = 200 \mathrm{~cm}$,$AC = 4 × 50 = 200 \mathrm{~cm}$,所以 $AB = AC = BC$,所以 $\triangle ABC$ 为等边三角形;
(2) 因为 $AD \perp BC$ 于 $D$,$\triangle ABC$ 为等边三角形,所以 $\angle ADB = 90^{\circ}$,$BD = \frac {1}{2}BC = 100$,在 $\mathrm{Rt} \triangle ABD$ 中,$AB^{2} = BD^{2} + AD^{2}$,所以 $AD = \sqrt {AB^{2} - BD^{2}} = \sqrt {200^{2} - 100^{2}} = 100 \sqrt {3}$,所以油桶的最高点到地面的距离 $= 25 + 100 \sqrt {3} + 25 = 50 + 100 \sqrt {3} \approx 223.2 (\mathrm{cm})$。答:遮雨棚的高度约为 $223.2 \mathrm{~cm}$。
查看更多完整答案,请扫码查看


