8. 如图,在平面直角坐标系中,直线$y = -2x + 6$分别与x轴,y轴交于A,B两点,将直线AB绕点A逆时针旋转$45^{\circ}$得到直线AC,过点B作$BD \perp AC$,垂足为点D,则点D的坐标是 (
A. $(-1,1)$
B. $(-\frac{3}{2},\frac{3}{2})$
C. $(-\frac{5}{3},\frac{5}{3})$
D. $(-\frac{5}{2},\frac{5}{2})$
B
)A. $(-1,1)$
B. $(-\frac{3}{2},\frac{3}{2})$
C. $(-\frac{5}{3},\frac{5}{3})$
D. $(-\frac{5}{2},\frac{5}{2})$
答案:
B
9. 一个正比例函数的图象过点$A(-2,4)$,则这个正比例函数的表达式是
y = -2x
。
答案:
y = -2x
10. 若一次函数$y = kx + 2 - k$不经过第二象限,则k的取值范围为
k ≥ 2
。
答案:
k ≥ 2
11. 甲、乙两车沿笔直公路同向行驶,车速分别为20m/s和25m/s。目前甲车在乙车前500m处,设$x\ \text{s}(0 \leqslant x \leqslant 100)$后两车相距y m,那么y关于x的函数表达式为
y = 500 - 5x(0 ≤ x ≤ 100)
。
答案:
y = 500 - 5x(0 ≤ x ≤ 100)
12. 如图,将直线OA向上平移2个单位长度,则平移后的直线的表达式为
y = 2x + 2
。
答案:
y = 2x + 2
13. 如图,已知一次函数$y = -x + 1$的图象与x轴、y轴分别交于点A,B,点M在y轴上(M不与原点重合),并且使以点A,B,M为顶点的三角形是等腰三角形,则M的坐标为
(0,1 + √2)、(0,1 - √2)或(0,-1)
。
答案:
(0,1 + √2)、(0,1 - √2)或(0,-1)
14. 如图,一次函数$y = kx - 3$的图象经过点M。
(1)求这个一次函数的表达式;
(2)判断点$(2,-7)$是否在该函数的图象上。
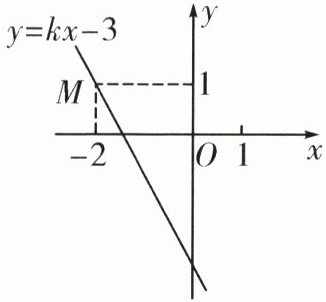
(1)求这个一次函数的表达式;
(2)判断点$(2,-7)$是否在该函数的图象上。
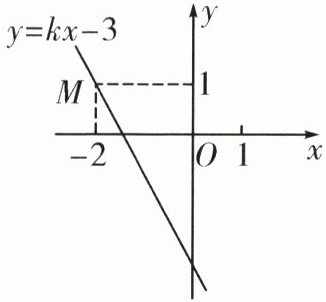
答案:
解:
(1)因为一次函数y = kx - 3的图象经过点M(-2,1),
所以 -2k - 3 = 1,
解得:k = -2,
所以这个一次函数表达式为y = -2x - 3;
(2)当x = 2时,y = -2×2 - 3 = -7,
所以点(2,-7)在该函数的图象上。
(1)因为一次函数y = kx - 3的图象经过点M(-2,1),
所以 -2k - 3 = 1,
解得:k = -2,
所以这个一次函数表达式为y = -2x - 3;
(2)当x = 2时,y = -2×2 - 3 = -7,
所以点(2,-7)在该函数的图象上。
查看更多完整答案,请扫码查看


