《2025年活页过关练习西安出版社九年级数学上册人教版》

1. 抛物线$y=-(x-1)^{2}+4$的顶点坐标是( )
A. $(1,4)$
B. $(1,-4)$
C. $(-1,4)$
D. $(-1,-4)$

答案： A

2. 剪纸是我国最古老的民间艺术之一. 下列剪纸图案中既是轴对称图形又是中心对称图形的是( )

答案： D

3. 点$P(a,-3)$关于原点对称的点是$P'(2,b)$，则$a+b$的值是( )
A. $-1$
B. $-5$
C. $1$
D. $5$

答案： C

4. 如图，在$\odot O$中，圆心角$∠AOB=2∠COD$，则$\overset{\frown}{AB}$与$\overset{\frown}{CD}$的关系是( )

A. $\overset{\frown}{AB}=2\overset{\frown}{CD}$
B. $\overset{\frown}{AB}=\overset{\frown}{CD}$
C. $\overset{\frown}{AB}＜2\overset{\frown}{CD}$
D. $2\overset{\frown}{AB}=\overset{\frown}{CD}$

答案： A

5. 某种植物的主干长出若干数目的枝干，每个枝干又长出同样数目的小分支，主干、枝干和小分支的总数是91. 设每个枝干长出$x$个小分支，则$x$满足的关系式为( )
A. $x+x^{2}=91$
B. $1+x^{2}=91$
C. $1+x+x^{2}=91$
D. $1+x(x-1)=91$

答案： C

6. 下列关于抛物线$y=-5(x+1)^{2}-3$的说法正确的是( )
A. 图象的对称轴为直线$x=1$
B. 函数的最大值是$-3$
C. 函数的最小值是$-3$
D. 顶点坐标为$(-1,3)$

答案： B

7. 如图，圆柱形水管内积水的水平面宽$AB=8cm$，水深$CD=2cm$，则水管的半径是( )

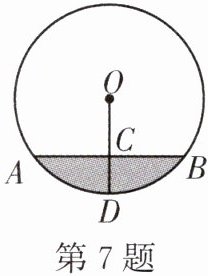
A. $4cm$
B. $5cm$
C. $6cm$
D. $7cm$

答案： B

8. 将抛物线$y=x^{2}-4$向右平移2个单位长度，再向上平移2个单位长度得到的抛物线的函数解析式为__________.

答案： $y=(x - 2)^2 - 2$

9. 已知$a$，$b$是一元二次方程$x^{2}+x-4=0$的两实根，则$a^{2}+ab+a$的值等于____.

答案： $0$

10. 已知圆锥的底面半径为$2cm$，母线长为$6cm$，则该圆锥的侧面积为______$cm^{2}$.

答案： $12\pi$

11. 如图，在正方形$ABCD$中，$E$，$F$是对角线$BD$上两点，将$\triangle ADF$绕点$A$顺时针旋转$90^{\circ}$后，得到$\triangle ABQ$，连接$AE$，$EQ$，若$BE=1$，$DF=2$，则$QE$的长为______.

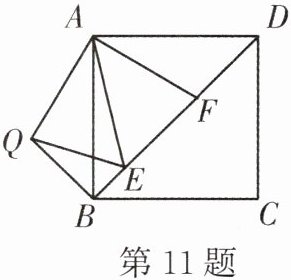
答案： $\boldsymbol{\sqrt{5}}$