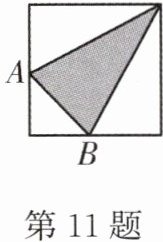
11. 小鹏制作了一个如图所示的靶盘,其中点A,B分别是边长为4cm的正方形靶盘相邻两边的中点,小鹏随意向该标靶区域投掷飞镖,则飞镖落在阴影区域的概率为____.

答案:
$\boldsymbol{\frac{3}{8}}$
12. (14分)[2024江西中考]某校一年级开设人数相同的A,B,C三个班级,甲、乙两位学生是该校一年级新生,开学初学校对所有一年级新生进行电脑随机分班.
(1)“学生甲分到A班”的概率是____;
(2)请用画树状图法或列表法,求甲、乙两位新生分到同一个班的概率.
(1)“学生甲分到A班”的概率是____;
(2)请用画树状图法或列表法,求甲、乙两位新生分到同一个班的概率.
答案:
【解析】:1. 因为有A,B,C三个班级且人数相同,随机分班,那么学生甲分到每个班的可能性是一样的,所以“学生甲分到A班”的概率是$\frac{1}{3}$。
2. 用列表法来求甲、乙两位新生分到同一个班的概率。列表如下:
| | A | B | C |
| --- | --- | --- | --- |
| A | (A,A) | (A,B) | (A,C) |
| B | (B,A) | (B,B) | (B,C) |
| C | (C,A) | (C,B) | (C,C) |
从表中可以看出,一共有9种等可能的结果,其中甲、乙两位新生分到同一个班的结果有3种,即(A,A)、(B,B)、(C,C),所以甲、乙两位新生分到同一个班的概率为$\frac{3}{9}=\frac{1}{3}$。
【答案】:1. $\frac{1}{3}$ 2. $\frac{1}{3}$
2. 用列表法来求甲、乙两位新生分到同一个班的概率。列表如下:
| | A | B | C |
| --- | --- | --- | --- |
| A | (A,A) | (A,B) | (A,C) |
| B | (B,A) | (B,B) | (B,C) |
| C | (C,A) | (C,B) | (C,C) |
从表中可以看出,一共有9种等可能的结果,其中甲、乙两位新生分到同一个班的结果有3种,即(A,A)、(B,B)、(C,C),所以甲、乙两位新生分到同一个班的概率为$\frac{3}{9}=\frac{1}{3}$。
【答案】:1. $\frac{1}{3}$ 2. $\frac{1}{3}$
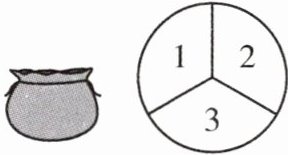
13. (20分)一个不透明的口袋中装有4个完全相同的小球,分别标有数字1,2,3,4. 另外有一个可以自由旋转的圆盘,被分成面积相等的3个扇形区域,分别标有数字1,2,3(如图所示). 小真从口袋中任意摸出一个小球,记下数字;小帅自由转动圆盘,记下指针指向的数字(若指针落在分割线上,则重新转动圆盘),然后计算摸出的小球和转出圆盘上的两个数的积.
(1)用列表或画树状图的方法,求摸出的小球和转出圆盘上的两个数的积为6的概率;
(2)小真和小帅想通过这个游戏来决定谁代表班级参加校外活动,他们约定:若这两个数的积为奇数,小真赢;否则,小帅赢. 你认为该游戏公平吗? 为什么? 如果不公平,请你修改游戏规则,使游戏公平.
(1)用列表或画树状图的方法,求摸出的小球和转出圆盘上的两个数的积为6的概率;
(2)小真和小帅想通过这个游戏来决定谁代表班级参加校外活动,他们约定:若这两个数的积为奇数,小真赢;否则,小帅赢. 你认为该游戏公平吗? 为什么? 如果不公平,请你修改游戏规则,使游戏公平.

答案:
【解析】:
(1)
列表如下:
|小球数字\圆盘数字|1|2|3|
|----|----|----|----|
|1|1×1 = 1|1×2 = 2|1×3 = 3|
|2|2×1 = 2|2×2 = 4|2×3 = 6|
|3|3×1 = 3|3×2 = 6|3×3 = 9|
|4|4×1 = 4|4×2 = 8|4×3 = 12|
一共有$4×3 = 12$种等可能的结果,其中积为$6$的有$2$种情况。
根据概率公式$P(A)=\frac{m}{n}$($m$是$A$发生的结果数,$n$是所有可能的结果数),所以积为$6$的概率$P=\frac{2}{12}=\frac{1}{6}$。
(2)
由
(1)中的列表可知,积为奇数的有$3$种情况,积为偶数的有$12 - 3 = 9$种情况。
小真赢的概率$P_1=\frac{3}{12}=\frac{1}{4}$,小帅赢的概率$P_2=\frac{9}{12}=\frac{3}{4}$。
因为$\frac{1}{4}\neq\frac{3}{4}$,所以游戏不公平。
修改规则:若这两个数的积小于$6$,小真赢;若这两个数的积大于$6$,小帅赢;若这两个数的积等于$6$,重新游戏(答案不唯一)。
【答案】:
(1)$\frac{1}{6}$
(2)不公平,因为小真赢的概率为$\frac{1}{4}$,小帅赢的概率为$\frac{3}{4}$,$\frac{1}{4}\neq\frac{3}{4}$。修改规则:若这两个数的积小于$6$,小真赢;若这两个数的积大于$6$,小帅赢;若这两个数的积等于$6$,重新游戏(答案不唯一)。
(1)
列表如下:
|小球数字\圆盘数字|1|2|3|
|----|----|----|----|
|1|1×1 = 1|1×2 = 2|1×3 = 3|
|2|2×1 = 2|2×2 = 4|2×3 = 6|
|3|3×1 = 3|3×2 = 6|3×3 = 9|
|4|4×1 = 4|4×2 = 8|4×3 = 12|
一共有$4×3 = 12$种等可能的结果,其中积为$6$的有$2$种情况。
根据概率公式$P(A)=\frac{m}{n}$($m$是$A$发生的结果数,$n$是所有可能的结果数),所以积为$6$的概率$P=\frac{2}{12}=\frac{1}{6}$。
(2)
由
(1)中的列表可知,积为奇数的有$3$种情况,积为偶数的有$12 - 3 = 9$种情况。
小真赢的概率$P_1=\frac{3}{12}=\frac{1}{4}$,小帅赢的概率$P_2=\frac{9}{12}=\frac{3}{4}$。
因为$\frac{1}{4}\neq\frac{3}{4}$,所以游戏不公平。
修改规则:若这两个数的积小于$6$,小真赢;若这两个数的积大于$6$,小帅赢;若这两个数的积等于$6$,重新游戏(答案不唯一)。
【答案】:
(1)$\frac{1}{6}$
(2)不公平,因为小真赢的概率为$\frac{1}{4}$,小帅赢的概率为$\frac{3}{4}$,$\frac{1}{4}\neq\frac{3}{4}$。修改规则:若这两个数的积小于$6$,小真赢;若这两个数的积大于$6$,小帅赢;若这两个数的积等于$6$,重新游戏(答案不唯一)。
查看更多完整答案,请扫码查看


