《2025年活页过关练习西安出版社九年级数学上册人教版》

13. (12分)已知二次函数$y = - x ^ { 2 } + b x + c$的图象经过点$( - 1, 4 )$,$( 1, 0 )$.
(1)求二次函数的解析式;
(2)在平面直角坐标系中,直接画出此二次函数的图象;
(3)结合函数图象,直接写出当$y \geqslant 0$时,$x$的取值范围.

答案： 【解析】：
(1)
已知二次函数$y = - x ^ { 2 } + b x + c$的图象经过点$( - 1, 4 )$，$( 1, 0 )$。
将点$( - 1, 4 )$代入函数得：$4=-(-1)^2 - b + c$，即$4=-1 - b + c$，移项可得$c - b = 5$ ①。
将点$( 1, 0 )$代入函数得：$0=-1^2 + b + c$，即$0=-1 + b + c$，移项可得$b + c = 1$ ②。
② - ①得：$(b + c)-(c - b)=1 - 5$，$b + c - c + b=-4$，$2b=-4$，解得$b=-2$。
把$b=-2$代入②得：$-2 + c = 1$，解得$c = 3$。
所以二次函数的解析式为$y=-x^2 - 2x + 3$。
(2)
对于二次函数$y=-x^2 - 2x + 3$，将其化为顶点式：
$\begin{aligned}y&=-x^2 - 2x + 3\\&=-(x^2 + 2x)+3\\&=-(x^2 + 2x + 1 - 1)+3\\&=-[(x + 1)^2 - 1]+3\\&=-(x + 1)^2 + 1 + 3\\&=-(x + 1)^2 + 4\end{aligned}$
所以其顶点坐标为$( - 1, 4 )$，对称轴为$x=-1$。
当$y = 0$时，$-x^2 - 2x + 3 = 0$，即$x^2 + 2x - 3 = 0$，分解因式得$(x + 3)(x - 1)=0$，解得$x=-3$或$x = 1$。
根据顶点坐标、对称轴以及与$x$轴交点坐标$(-3,0)$，$(1,0)$，可画出函数图象（略）。
(3)
由函数图象可知，当$y\geqslant0$时，$x$的取值范围是$-3\leqslant x\leqslant1$。
【答案】：
(1)$y=-x^2 - 2x + 3$
(2)略
(3)$-3\leqslant x\leqslant1$

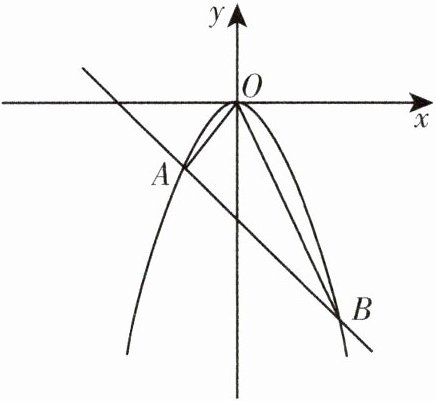
14. (16分)如图,在平面直角坐标系$x O y$中,二次函数$y = a x ^ { 2 } ( a \neq 0 )$与一次函数$y = k x - 2$的图象相交于$A$,$B$两点,其中$A ( - 1, - 1 )$.
(1)求$a$,$k$的值;
(2)求$\triangle O A B$的面积;
(3)$P$是第四象限直线$AB$上方抛物线上一个动点,过点$P$作$x$轴的垂线交直线$AB$于点$M$,当$P M = 2$时,求点$P$的坐标.

答案： 【解析】：
(1)
把$A(-1,-1)$代入$y = ax^{2}$，可得$-1=a\times(-1)^{2}$，即$a = - 1$。
把$A(-1,-1)$代入$y=kx - 2$，可得$-1=-k - 2$，移项得$k=-2 + 1=-1$。
(2)
由
(1)知一次函数解析式为$y=-x - 2$，令$y = 0$，则$0=-x - 2$，解得$x=-2$，所以直线$y=-x - 2$与$x$轴交点$C$的坐标为$(-2,0)$。
联立$\begin{cases}y=-x^{2}\\y=-x - 2\end{cases}$，即$-x^{2}=-x - 2$，移项得$x^{2}-x - 2 = 0$，分解因式$(x + 1)(x - 2)=0$，解得$x_{1}=-1$，$x_{2}=2$。
当$x = 2$时，$y=-2 - 2=-4$，所以$B(2,-4)$。
根据三角形面积公式$S_{\triangle OAB}=S_{\triangle AOC}+S_{\triangle BOC}$，$S_{\triangle AOC}=\frac{1}{2}\times| - 2|\times| - 1| = 1$，$S_{\triangle BOC}=\frac{1}{2}\times| - 2|\times| - 4| = 4$，所以$S_{\triangle OAB}=1 + 4=3$。
(3)
设$P(x,-x^{2})$，因为$PM\perp x$轴，所以$M(x,-x - 2)$。
因为$P$在第四象限直线$AB$上方抛物线上，所以$PM=-x^{2}-(-x - 2)$。
已知$PM = 2$，则$-x^{2}+x + 2 = 2$，移项得$x^{2}-x = 0$，分解因式$x(x - 1)=0$，解得$x_{1}=0$（舍去，因为$P$在第四象限），$x_{2}=1$。
当$x = 1$时，$y=-1^{2}=-1$，所以$P(1,-1)$。
【答案】：
(1)$a=-1$，$k=-1$；
(2)$3$；
(3)$(1,-1)$。