《2025年活页过关练习西安出版社九年级数学上册人教版》

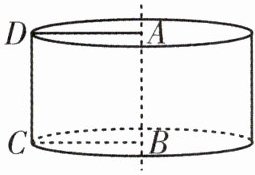
1. [教材原题]如图，已知矩形ABCD的周长为36 cm，矩形绕它的一条边AB旋转形成一个圆柱，边AB长为多少时，旋转形成的圆柱的侧面积S最大?

答案： 【解析】：
设$AB = x cm$，则$BC=(18 - x)cm$。
圆柱侧面积公式$S = 2\pi rh$（这里$r = BC$，$h = AB$），所以$S = 2\pi\times(18 - x)\times x$。
展开得$S=-2\pi x^{2}+36\pi x$，对于二次函数$y = ax^{2}+bx + c$（$a\neq0$），这里$a=-2\pi$，$b = 36\pi$。
根据二次函数顶点坐标公式$x=-\frac{b}{2a}$，可得$x =-\frac{36\pi}{2\times(-2\pi)} = 9$。
因为$a=-2\pi\lt0$，所以二次函数图象开口向下，当$x = 9$时，$S$有最大值。
【答案】：
当边$AB$长为$9cm$时，旋转形成的圆柱的侧面积$S$最大。

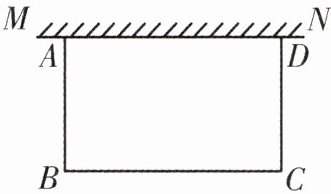
2. [变式]如图，在足够大的空地上有一段长为a m的旧墙MN，某人利用旧墙和木栏围成一个矩形菜园ABCD，其中AD≤MN，已知矩形菜园的一边靠墙，另三边一共用了100 m木栏. 求矩形菜园ABCD面积的最大值.

答案： 【解析】：设$AD = xm(0\lt x\leq a)$，则$AB=\frac{100 - x}{2}m$。
根据矩形面积公式$S = AB\times AD$，可得$S=\frac{100 - x}{2}\times x=-\frac{1}{2}x^{2}+50x$。
对于二次函数$y =-\frac{1}{2}x^{2}+50x$，其对称轴为$x =-\frac{50}{2\times(-\frac{1}{2})}=50$，二次项系数$-\frac{1}{2}\lt0$，函数图象开口向下。
当$a\geq50$时：
在对称轴$x = 50$处取得最大值，$S_{max}=-\frac{1}{2}\times50^{2}+50\times50 = 1250(m^{2})$。
当$0\lt a\lt50$时：
函数$S =-\frac{1}{2}x^{2}+50x$在$(0,a]$上单调递增，所以当$x = a$时，$S_{max}=-\frac{1}{2}a^{2}+50a(m^{2})$。
【答案】：当$a\geq50$时，矩形菜园$ABCD$面积的最大值为$1250m^{2}$；当$0\lt a\lt50$时，矩形菜园$ABCD$面积的最大值为$(-\frac{1}{2}a^{2}+50a)m^{2}$。

3. [变式]如图，在矩形ABCD中，AB=18 cm，AD=4 cm，点P，Q分别从A，B同时出发，点P在边AB上沿AB方向以每秒2 cm的速度匀速运动，点Q在边BC上沿BC方向以每秒1 cm的速度匀速运动，当点Q到达点C时，两点同时停止运动. 设运动时间为x秒，△PBQ的面积为y cm²，求△PBQ面积的最大值.

答案： 【解析】：
已知$AB = 18cm$，点$P$的速度是每秒$2cm$，运动时间为$x$秒，则$AP = 2x cm$，那么$PB=(18 - 2x)cm$。
又因为点$Q$的速度是每秒$1cm$，运动时间为$x$秒，且$BC = AD = 4cm$（矩形对边相等），所以$BQ = x cm$。
根据三角形面积公式$S=\frac{1}{2}ah$（这里$a = PB$，$h = BQ$），可得$y=\frac{1}{2}(18 - 2x)x$。
化简$y=\frac{1}{2}(18 - 2x)x$：
$\begin{aligned}y&=\frac{1}{2}(18x-2x^{2})\\&=-x^{2}+9x\\&=-x^{2}+9x-\frac{81}{4}+\frac{81}{4}\\&=-(x - \frac{9}{2})^{2}+\frac{81}{4}\end{aligned}$
因为点$Q$到达点$C$时停止运动，$BC = 4cm$，点$Q$速度是$1cm/s$，所以$0\leq x\leq4$。
对于二次函数$y =-(x - \frac{9}{2})^{2}+\frac{81}{4}$，其图象开口向下，对称轴为$x=\frac{9}{2}$，在对称轴左侧$y$随$x$的增大而增大。
所以当$x = 4$时，$y$有最大值。
把$x = 4$代入$y=-x^{2}+9x$得：$y=-4^{2}+9\times4=-16 + 36=20$。
【答案】：$20cm^{2}$