1. [教材改编]有一个抛物线形的拱形桥洞,桥洞离水面的最大高度为 4m,跨度为 10m,如图所示,把它的图形放在平面直角坐标系中.
(1)求抛物线的函数解析式;
(2)在对称轴右边 1m 处,桥洞离水面的高是多少?

(1)求抛物线的函数解析式;
(2)在对称轴右边 1m 处,桥洞离水面的高是多少?

答案:
【解析】:
(1) 已知抛物线顶点坐标为$(5,4)$,设抛物线的函数解析式为$y = a(x - 5)^2+4$。
因为抛物线过点$(0,0)$,把$(0,0)$代入$y = a(x - 5)^2+4$得:
$0=a(0 - 5)^2+4$,即$25a+4 = 0$,解得$a=-\frac{4}{25}$。
所以抛物线的函数解析式为$y = -\frac{4}{25}(x - 5)^2+4=-\frac{4}{25}x^{2}+\frac{8}{5}x$。
(2) 当$x = 5 + 1=6$时,把$x = 6$代入$y = -\frac{4}{25}(x - 5)^2+4$得:
$y=-\frac{4}{25}(6 - 5)^2+4=-\frac{4}{25}+4=\frac{96}{25}=3.84$(m)
【答案】:
(1)$y = -\frac{4}{25}x^{2}+\frac{8}{5}x$;
(2)$3.84m$。
(1) 已知抛物线顶点坐标为$(5,4)$,设抛物线的函数解析式为$y = a(x - 5)^2+4$。
因为抛物线过点$(0,0)$,把$(0,0)$代入$y = a(x - 5)^2+4$得:
$0=a(0 - 5)^2+4$,即$25a+4 = 0$,解得$a=-\frac{4}{25}$。
所以抛物线的函数解析式为$y = -\frac{4}{25}(x - 5)^2+4=-\frac{4}{25}x^{2}+\frac{8}{5}x$。
(2) 当$x = 5 + 1=6$时,把$x = 6$代入$y = -\frac{4}{25}(x - 5)^2+4$得:
$y=-\frac{4}{25}(6 - 5)^2+4=-\frac{4}{25}+4=\frac{96}{25}=3.84$(m)
【答案】:
(1)$y = -\frac{4}{25}x^{2}+\frac{8}{5}x$;
(2)$3.84m$。
2. [变式][2024 陕西中考]某广场的声控喷泉是由若干个垂直于地面的柱形喷泉装置组成的. 每个柱形喷泉装置上都有上下两个喷头,这两个喷头朝向一致,喷出的水流均呈抛物线形. 当围观游人喊声较小时,下喷头喷水;当围观游人喊声较大时,上下两个喷头都喷水. 如图所示,点 A 和点 B 是一个柱形喷泉装置 OB 上的两个喷头,A 喷头喷出的水流的落地点为 C. 以 O 为原点,以 OC 所在直线为 x 轴,OB 所在直线为 y 轴,建立平面直角坐标系(柱形喷泉装置的粗细忽略不计). 已知 OA=1m,OB=2m,OC=3m,从 A 喷头和 B 喷头各喷出的水流的高度 y(m)与水平距离 x(m)之间的关系式分别是 $ y = -\frac{1}{3}x^{2} + bx + c $ 和 $ y = -\frac{1}{3}x^{2} + bx + c' $.
(1)求 A 喷头喷出的水流的最大高度;
(2)一名游人站在点 D 处,OD=4m. 当围观游人喊声较大时,B 喷头喷出的水流是否会落在该游人所站的点 D 处?
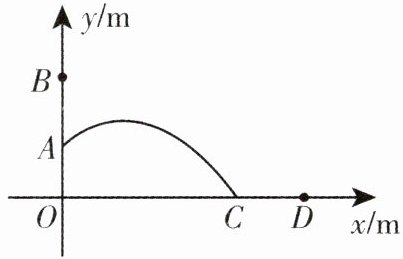
(1)求 A 喷头喷出的水流的最大高度;
(2)一名游人站在点 D 处,OD=4m. 当围观游人喊声较大时,B 喷头喷出的水流是否会落在该游人所站的点 D 处?

答案:
【解析】:
(1)已知$OA = 1m$,$OC = 3m$,则$A(0,1)$,$C(3,0)$。
把$A(0,1)$,$C(3,0)$代入$y = -\frac{1}{3}x^{2}+bx + c$中,可得$\begin{cases}c = 1\\-\frac{1}{3}\times3^{2}+3b + c = 0\end{cases}$。
将$c = 1$代入$-\frac{1}{3}\times3^{2}+3b + c = 0$,即$-3 + 3b+1 = 0$,$3b = 2$,解得$b=\frac{2}{3}$。
所以$A$喷头喷出水流的关系式为$y = -\frac{1}{3}x^{2}+\frac{2}{3}x + 1$。
对于二次函数$y = ax^{2}+bx + c(a\neq0)$,其对称轴为$x = -\frac{b}{2a}$,这里$a = -\frac{1}{3}$,$b=\frac{2}{3}$,对称轴$x = -\frac{\frac{2}{3}}{2\times(-\frac{1}{3})}=1$。
把$x = 1$代入$y = -\frac{1}{3}x^{2}+\frac{2}{3}x + 1$,$y=-\frac{1}{3}\times1^{2}+\frac{2}{3}\times1 + 1=-\frac{1}{3}+\frac{2}{3}+1=\frac{4}{3}(m)$。
(2)已知$OB = 2m$,则$B(0,2)$。
把$B(0,2)$代入$y = -\frac{1}{3}x^{2}+\frac{2}{3}x + c'$中,可得$c' = 2$,所以$B$喷头喷出水流的关系式为$y = -\frac{1}{3}x^{2}+\frac{2}{3}x + 2$。
当$y = 0$时,$-\frac{1}{3}x^{2}+\frac{2}{3}x + 2 = 0$,方程两边同时乘以$-3$得$x^{2}-2x - 6 = 0$。
根据一元二次方程$ax^{2}+bx + c = 0(a\neq0)$的求根公式$x=\frac{-b\pm\sqrt{b^{2}-4ac}}{2a}$,这里$a = 1$,$b=-2$,$c=-6$,则$x=\frac{2\pm\sqrt{(-2)^{2}-4\times1\times(-6)}}{2\times1}=\frac{2\pm\sqrt{4 + 24}}{2}=\frac{2\pm\sqrt{28}}{2}=1\pm\sqrt{7}$。
因为$x\gt0$,所以$x = 1+\sqrt{7}\approx1 + 2.65 = 3.65\lt4$。
【答案】:
(1)$\frac{4}{3}m$
(2)不会。
(1)已知$OA = 1m$,$OC = 3m$,则$A(0,1)$,$C(3,0)$。
把$A(0,1)$,$C(3,0)$代入$y = -\frac{1}{3}x^{2}+bx + c$中,可得$\begin{cases}c = 1\\-\frac{1}{3}\times3^{2}+3b + c = 0\end{cases}$。
将$c = 1$代入$-\frac{1}{3}\times3^{2}+3b + c = 0$,即$-3 + 3b+1 = 0$,$3b = 2$,解得$b=\frac{2}{3}$。
所以$A$喷头喷出水流的关系式为$y = -\frac{1}{3}x^{2}+\frac{2}{3}x + 1$。
对于二次函数$y = ax^{2}+bx + c(a\neq0)$,其对称轴为$x = -\frac{b}{2a}$,这里$a = -\frac{1}{3}$,$b=\frac{2}{3}$,对称轴$x = -\frac{\frac{2}{3}}{2\times(-\frac{1}{3})}=1$。
把$x = 1$代入$y = -\frac{1}{3}x^{2}+\frac{2}{3}x + 1$,$y=-\frac{1}{3}\times1^{2}+\frac{2}{3}\times1 + 1=-\frac{1}{3}+\frac{2}{3}+1=\frac{4}{3}(m)$。
(2)已知$OB = 2m$,则$B(0,2)$。
把$B(0,2)$代入$y = -\frac{1}{3}x^{2}+\frac{2}{3}x + c'$中,可得$c' = 2$,所以$B$喷头喷出水流的关系式为$y = -\frac{1}{3}x^{2}+\frac{2}{3}x + 2$。
当$y = 0$时,$-\frac{1}{3}x^{2}+\frac{2}{3}x + 2 = 0$,方程两边同时乘以$-3$得$x^{2}-2x - 6 = 0$。
根据一元二次方程$ax^{2}+bx + c = 0(a\neq0)$的求根公式$x=\frac{-b\pm\sqrt{b^{2}-4ac}}{2a}$,这里$a = 1$,$b=-2$,$c=-6$,则$x=\frac{2\pm\sqrt{(-2)^{2}-4\times1\times(-6)}}{2\times1}=\frac{2\pm\sqrt{4 + 24}}{2}=\frac{2\pm\sqrt{28}}{2}=1\pm\sqrt{7}$。
因为$x\gt0$,所以$x = 1+\sqrt{7}\approx1 + 2.65 = 3.65\lt4$。
【答案】:
(1)$\frac{4}{3}m$
(2)不会。
查看更多完整答案,请扫码查看


