《2025年活页过关练习西安出版社九年级数学上册人教版》

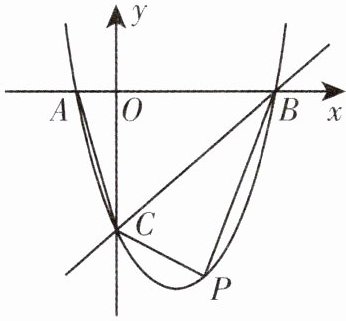
1. [教材改编]如图，在平面直角坐标系 $ xOy $ 中，二次函数 $ y = x ^ { 2 } - 2 x - 3 $ 的图象与 $ x $ 轴交于 $ A $，$ B $ 两点，与 $ y $ 轴交于点 $ C $，动点 $ P $ 在直线 $ BC $ 下方的抛物线上，求四边形 $ ABPC $ 面积的最大值.

答案： 【解析】：
首先求$A$、$B$、$C$的坐标：
对于二次函数$y = x^{2}-2x - 3$，令$y = 0$，即$x^{2}-2x - 3 = 0$，分解因式得$(x - 3)(x + 1)=0$，解得$x_{1}=3$，$x_{2}=-1$，所以$A(-1,0)$，$B(3,0)$。
令$x = 0$，则$y=-3$，所以$C(0,-3)$。
直线$BC$的解析式：设直线$BC$的解析式为$y = kx + b$，把$B(3,0)$，$C(0,-3)$代入得$\begin{cases}3k + b = 0\\b=-3\end{cases}$，解得$\begin{cases}k = 1\\b=-3\end{cases}$，所以直线$BC$的解析式为$y = x - 3$。
设$P(x,x^{2}-2x - 3)(0\lt x\lt3)$，过点$P$作$PD\perp x$轴交$BC$于点$D$，则$D(x,x - 3)$。
所以$PD=(x - 3)-(x^{2}-2x - 3)=-x^{2}+3x$。
$S_{\triangle BPC}=\frac{1}{2}PD\cdot OB=\frac{1}{2}\times(-x^{2}+3x)\times3=-\frac{3}{2}x^{2}+\frac{9}{2}x$。
$S_{\triangle ABC}=\frac{1}{2}AB\cdot OC$，$AB = 3-(-1)=4$，$OC = 3$，所以$S_{\triangle ABC}=\frac{1}{2}\times4\times3 = 6$。
则$S_{四边形ABPC}=S_{\triangle ABC}+S_{\triangle BPC}=6-\frac{3}{2}x^{2}+\frac{9}{2}x$。
对于二次函数$S =-\frac{3}{2}x^{2}+\frac{9}{2}x + 6$，$a =-\frac{3}{2}\lt0$，对称轴为$x =-\frac{\frac{9}{2}}{2\times(-\frac{3}{2})}=\frac{3}{2}$。
当$x=\frac{3}{2}$时，$S_{四边形ABPC}$有最大值，$S_{max}=-\frac{3}{2}\times(\frac{3}{2})^{2}+\frac{9}{2}\times\frac{3}{2}+6=-\frac{27}{8}+\frac{27}{4}+6=\frac{-27 + 54 + 48}{8}=\frac{75}{8}$。
【答案】：$\frac{75}{8}$

2. [变式][2024 福州一检改编]已知抛物线 $ y = - x ^ { 2 } + 2 x + 3 $ 与 $ x $ 轴交于 $ A $，$ B $ 两点(点 $ A $ 在点 $ B $ 的左侧)，与 $ y $ 轴交于点 $ C $. 若 $ P $ 是抛物线上的一点，且 $ \triangle APC $ 的面积为 $ \triangle APB $ 面积的 2 倍，求点 $ P $ 的坐标.

答案： 【解析】：
1. 首先，求抛物线与坐标轴的交点坐标：
对于抛物线$y = -x^{2}+2x + 3$，令$y = 0$，则$-x^{2}+2x + 3 = 0$，即$x^{2}-2x - 3 = 0$。
分解因式得$(x - 3)(x+1)=0$，解得$x_1=-1$，$x_2 = 3$。
因为点$A$在点$B$的左侧，所以$A(-1,0)$，$B(3,0)$。
令$x = 0$，则$y = 3$，所以$C(0,3)$。
2. 然后，设点$P$的坐标为$(x,y)$：
根据三角形面积公式$S=\frac{1}{2}\times底\times高$。
$\triangle APB$以$AB$为底，$AB=3 - (-1)=4$，$\triangle APB$的高为$\vert y_{P}\vert$（$y_{P}$是点$P$的纵坐标），所以$S_{\triangle APB}=\frac{1}{2}\times AB\times\vert y_{P}\vert=\frac{1}{2}\times4\times\vert y\vert = 2\vert y\vert$。
$\triangle APC$可以以$AC$为底，先求$AC$的长度，根据两点间距离公式$d=\sqrt{(x_2 - x_1)^{2}+(y_2 - y_1)^{2}}$，$A(-1,0)$，$C(0,3)$，则$AC=\sqrt{(0 + 1)^{2}+(3 - 0)^{2}}=\sqrt{1 + 9}=\sqrt{10}$。
点$P(x,y)$到直线$AC$的距离$h$，先求直线$AC$的方程，直线$AC$的斜率$k=\frac{3-0}{0 + 1}=3$，根据点斜式$y - y_1=k(x - x_1)$，直线$AC$的方程为$y-0 = 3(x + 1)$，即$3x-y+3 = 0$。
根据点$(x_0,y_0)$到直线$Ax+By + C = 0$的距离公式$d=\frac{\vert Ax_0+By_0 + C\vert}{\sqrt{A^{2}+B^{2}}}$，点$P(x,y)$到直线$3x - y+3 = 0$的距离$h=\frac{\vert 3x - y+3\vert}{\sqrt{3^{2}+(-1)^{2}}}=\frac{\vert 3x - y+3\vert}{\sqrt{10}}$，则$S_{\triangle APC}=\frac{1}{2}\times AC\times h=\frac{1}{2}\times\sqrt{10}\times\frac{\vert 3x - y+3\vert}{\sqrt{10}}=\frac{1}{2}\vert 3x - y+3\vert$。
另一种方法，$\triangle APC$也可以以$AO$为底（$O$为坐标原点），$AO = 1$，$\triangle APC$的面积可以表示为$S_{\triangle APC}=S_{\triangle AOC}+S_{\triangle POC}-S_{\triangle AOP}$。
$S_{\triangle AOC}=\frac{1}{2}\times AO\times OC=\frac{1}{2}\times1\times3=\frac{3}{2}$，$S_{\triangle POC}=\frac{1}{2}\times OC\times\vert x\vert=\frac{1}{2}\times3\times\vert x\vert$，$S_{\triangle AOP}=\frac{1}{2}\times AO\times\vert y\vert=\frac{1}{2}\times1\times\vert y\vert$。
所以$S_{\triangle APC}=\frac{3}{2}+\frac{3}{2}\vert x\vert-\frac{1}{2}\vert y\vert$。
已知$S_{\triangle APC}=2S_{\triangle APB}$，即$\frac{3}{2}+\frac{3}{2}\vert x\vert-\frac{1}{2}\vert y\vert=2\times2\vert y\vert$，$\frac{3}{2}+\frac{3}{2}\vert x\vert-\frac{1}{2}\vert y\vert = 4\vert y\vert$，$\frac{3}{2}+\frac{3}{2}\vert x\vert=\frac{9}{2}\vert y\vert$，$1+\vert x\vert = 3\vert y\vert$。
因为$y=-x^{2}+2x + 3$，分情况讨论：
当$y\gt0$时，$1+\vert x\vert = 3y$。
若$x\geqslant0$，则$1 + x=3(-x^{2}+2x + 3)$，即$1 + x=-3x^{2}+6x + 9$，$3x^{2}-5x - 8 = 0$。
分解因式得$(3x - 8)(x + 1)=0$，解得$x_1=-1$（与点$A$重合，舍去），$x_2=\frac{8}{3}$。
当$x=\frac{8}{3}$时，$y=-(\frac{8}{3})^{2}+2\times\frac{8}{3}+3=-\frac{64}{9}+\frac{16}{3}+3=-\frac{64}{9}+\frac{48}{9}+\frac{27}{9}=\frac{-64 + 48+27}{9}=\frac{11}{9}$。
若$x\lt0$，则$1 - x=3(-x^{2}+2x + 3)$，即$1 - x=-3x^{2}+6x + 9$，$3x^{2}-7x - 8 = 0$。
根据求根公式$x=\frac{7\pm\sqrt{(-7)^{2}-4\times3\times(-8)}}{2\times3}=\frac{7\pm\sqrt{49 + 96}}{6}=\frac{7\pm\sqrt{145}}{6}$，$x=\frac{7-\sqrt{145}}{6}$（$x=\frac{7 + \sqrt{145}}{6}\gt0$舍去）。
当$x=\frac{7-\sqrt{145}}{6}$时，$y=-(\frac{7-\sqrt{145}}{6})^{2}+2\times\frac{7-\sqrt{145}}{6}+3$。
当$y\lt0$时，$1+\vert x\vert=-3y$。
若$x\geqslant0$，则$1 + x=-3(-x^{2}+2x + 3)$，即$1 + x = 3x^{2}-6x - 9$，$3x^{2}-7x - 10 = 0$。
分解因式得$(3x - 10)(x + 1)=0$，解得$x_1=-1$（与点$A$重合，舍去），$x_2=\frac{10}{3}$。
当$x=\frac{10}{3}$时，$y=-(\frac{10}{3})^{2}+2\times\frac{10}{3}+3=-\frac{100}{9}+\frac{20}{3}+3=-\frac{100}{9}+\frac{60}{9}+\frac{27}{9}=-\frac{13}{9}$。
若$x\lt0$，则$1 - x=-3(-x^{2}+2x + 3)$，即$1 - x = 3x^{2}-6x - 9$，$3x^{2}-5x - 10 = 0$。
根据求根公式$x=\frac{5\pm\sqrt{(-5)^{2}-4\times3\times(-10)}}{2\times3}=\frac{5\pm\sqrt{25 + 120}}{6}=\frac{5\pm\sqrt{145}}{6}$，$x=\frac{5-\sqrt{145}}{6}$。
当$x=\frac{5-\sqrt{145}}{6}$时，$y=-(\frac{5-\sqrt{145}}{6})^{2}+2\times\frac{5-\sqrt{145}}{6}+3$。
【答案】：$(\frac{8}{3},\frac{11}{9})$，$(\frac{7 - \sqrt{145}}{6},-(\frac{7 - \sqrt{145}}{6})^{2}+2\times\frac{7 - \sqrt{145}}{6}+3)$，$(\frac{10}{3},-\frac{13}{9})$，$(\frac{5 - \sqrt{145}}{6},-(\frac{5 - \sqrt{145}}{6})^{2}+2\times\frac{5 - \sqrt{145}}{6}+3)$