《2025年活页过关练习西安出版社九年级数学上册人教版》

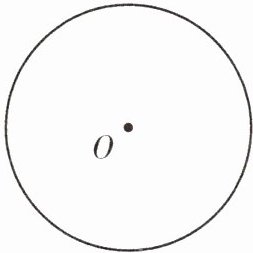
1. [教材改编]已知$\odot O$及圆外一点$P$.
(1)尺规作图:过点$P$作$\odot O$的两条切线$PA$,$PB$,切点分别是点$A$,点$B$;(保留作图痕迹,不写作法)
(2)连接$AO$并延长,交$\odot O$于点$D$,连接$BD$,$\angle ADB = 70^{\circ}$,求$\angle APB$的度数.

答案： 【解析】：
(1) 略（按照尺规作圆的切线步骤作图，连接$OP$，作$OP$的垂直平分线，以$OP$中点为圆心，$\frac{1}{2}OP$为半径画弧交$\odot O$于$A$、$B$，连接$PA$、$PB$）。
(2) 连接$AB$，因为$AD$是$\odot O$的直径，所以$\angle ABD = 90^{\circ}$（直径所对的圆周角是直角）。
在$Rt\triangle ABD$中，$\angle DAB=180^{\circ}-\angle ABD - \angle ADB=180^{\circ}-90^{\circ}-70^{\circ}=20^{\circ}$。
因为$PA$、$PB$是$\odot O$的切线，所以$OA\perp PA$，即$\angle OAP = 90^{\circ}$，$\angle PAB=\angle OAP-\angle DAB = 90^{\circ}-20^{\circ}=70^{\circ}$。
又因为$PA = PB$（切线长定理：从圆外一点引圆的两条切线，它们的切线长相等），所以$\triangle PAB$是等腰三角形，$\angle PAB=\angle PBA = 70^{\circ}$。
根据三角形内角和定理$\angle APB=180^{\circ}-\angle PAB-\angle PBA=180^{\circ}-70^{\circ}-70^{\circ}=40^{\circ}$。
【答案】：
(1) 略。
(2)$40^{\circ}$。

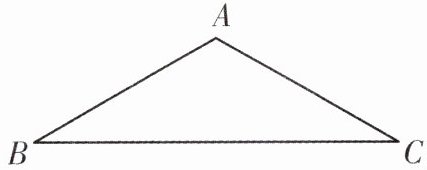
2. [变式]如图,在$\triangle ABC$中,$\angle B = \angle C = 30^{\circ}$.
(1)求作$\odot O$,使圆心$O$落在$BC$边上,且$\odot O$经过$A$,$B$两点;(尺规作图,保留作图痕迹,不写作法)
(2)已知$BC = 6$,求$\odot O$的半径.

答案： 【解析】：
(1) 作线段 $AB$ 的垂直平分线，交 $BC$ 于点 $O$，以 $O$ 为圆心，$OB$ 长为半径作圆，则$\odot O$ 即为所求（作图痕迹略）。
(2) 连接 $OA$。
因为 $OA = OB$，所以$\angle OAB=\angle B = 30^{\circ}$。
又因为$\angle B=\angle C = 30^{\circ}$，所以$\angle BAC=180^{\circ}-\angle B - \angle C=120^{\circ}$。
则$\angle OAC=\angle BAC-\angle OAB = 120^{\circ}-30^{\circ}=90^{\circ}$。
设$\odot O$ 的半径为 $r$，则 $OB = OA = r$，$OC=BC - OB=6 - r$。
在$Rt\triangle AOC$中，$\angle C = 30^{\circ}$，根据直角三角形中$30^{\circ}$所对的直角边是斜边的一半，可得$OA=\frac{1}{2}OC$，即$r=\frac{1}{2}(6 - r)$。
解方程$r=\frac{1}{2}(6 - r)$：
$\begin{aligned}r&=\frac{1}{2}(6 - r)\\2r&=6 - r\\2r+r&=6\\3r&=6\\r&=2\end{aligned}$
【答案】：
(1) 作图略。
(2) $2$ 。

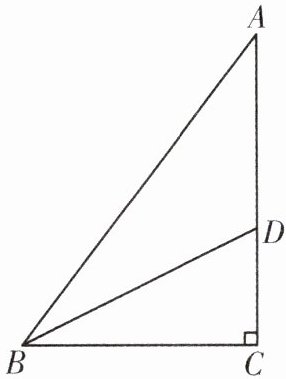
3. [变式]如图,在$Rt\triangle ABC$中,$\angle C = 90^{\circ}$,$BD$平分$\angle ABC$交$AC$于点$D$,$O$是$AB$上一点,且$\odot O$经过$B$,$D$两点,分别交$AB$,$BC$于点$E$,$F$.
(1)使用直尺和圆规,根据题目要求补全图形;(保留作图痕迹,不写作法)
(2)求证:$\odot O$与$AC$相切.

答案： 【解析】：
(1) 连接 $BD$，作 $BD$ 的垂直平分线交 $AB$ 于点 $O$，以 $O$ 为圆心，$OB$ 长为半径画圆，即可补全图形。
(2) 连接 $OD$。
因为 $OB = OD$，所以 $\angle OBD=\angle ODB$。
又因为 $BD$ 平分 $\angle ABC$，所以 $\angle OBD = \angle DBC$。
则 $\angle ODB=\angle DBC$，所以 $OD// BC$。
因为 $\angle C = 90^{\circ}$，即 $BC\perp AC$，根据两直线平行，同位角相等，可得 $OD\perp AC$。
又因为 $OD$ 是 $\odot O$ 的半径，所以 $\odot O$ 与 $AC$ 相切。
【答案】：
(1) 补全图形如上述解析步骤。
(2) 证明过程如上述解析步骤，即证得 $\odot O$ 与 $AC$ 相切。