1. [教材原题]如图,$\triangle ABD$,$\triangle AEC$都是等边三角形. $BE$与$DC$有什么关系?你能用旋转的性质说明上述关系成立的理由吗?


答案:
【解析】:
因为$\triangle ABD$,$\triangle AEC$都是等边三角形,所以$AD = AB$,$AC = AE$,$\angle BAD=\angle CAE = 60^{\circ}$。
$\angle BAD+\angle BAC=\angle CAE+\angle BAC$,即$\angle DAC=\angle BAE$。
在$\triangle DAC$和$\triangle BAE$中,$\begin{cases}AD = AB\\\angle DAC=\angle BAE\\AC = AE\end{cases}$,根据$SAS$(边角边)定理可得$\triangle DAC\cong\triangle BAE$,所以$BE = DC$。
从旋转的性质来看,$\triangle BAE$可以看作是$\triangle DAC$绕点$A$顺时针旋转$60^{\circ}$得到的(因为$\angle BAD = 60^{\circ}$),根据旋转的性质,旋转前后的图形全等,所以对应边$BE = DC$。
【答案】:$BE = DC$
因为$\triangle ABD$,$\triangle AEC$都是等边三角形,所以$AD = AB$,$AC = AE$,$\angle BAD=\angle CAE = 60^{\circ}$。
$\angle BAD+\angle BAC=\angle CAE+\angle BAC$,即$\angle DAC=\angle BAE$。
在$\triangle DAC$和$\triangle BAE$中,$\begin{cases}AD = AB\\\angle DAC=\angle BAE\\AC = AE\end{cases}$,根据$SAS$(边角边)定理可得$\triangle DAC\cong\triangle BAE$,所以$BE = DC$。
从旋转的性质来看,$\triangle BAE$可以看作是$\triangle DAC$绕点$A$顺时针旋转$60^{\circ}$得到的(因为$\angle BAD = 60^{\circ}$),根据旋转的性质,旋转前后的图形全等,所以对应边$BE = DC$。
【答案】:$BE = DC$
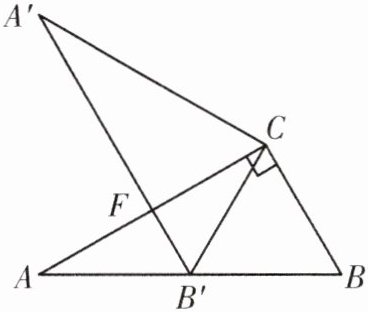
2. [变式]如图,在$Rt\triangle ABC$中,$\angle ACB=90^{\circ}$,$\angle A=30^{\circ}$,将$\triangle ABC$绕点$C$顺时针旋转得到$\triangle A^{\prime}B^{\prime}C$,点$B^{\prime}$恰好落在$AB$边上,$A^{\prime}B^{\prime}$交$AC$于点$F$. $AC$和$A^{\prime}B^{\prime}$有什么样的位置关系?并说明理由.

答案:
【解析】:
- 因为在$Rt\triangle ABC$中,$\angle ACB = 90^{\circ}$,$\angle A = 30^{\circ}$,所以$\angle B = 60^{\circ}$。
- 由旋转可知$CB = CB^{\prime}$,所以$\triangle BCB^{\prime}$是等边三角形,则$\angle BCB^{\prime}=60^{\circ}$。
- 那么$\angle A^{\prime}CA = 180^{\circ}-\angle BCB^{\prime}-\angle ACB = 180^{\circ}- 60^{\circ}-90^{\circ}=30^{\circ}$。
- 又因为$\angle A^{\prime}=\angle A = 30^{\circ}$,所以$\angle A^{\prime}FC = 180^{\circ}-\angle A^{\prime}-\angle A^{\prime}CA = 180^{\circ}-30^{\circ}-30^{\circ}=120^{\circ}$,$\angle AFC = 180^{\circ}-\angle A^{\prime}FC = 60^{\circ}$。
- 而$\angle A^{\prime}CA = 30^{\circ}$,所以$\angle A^{\prime}FC = 90^{\circ}$,即$AC\perp A^{\prime}B^{\prime}$。
【答案】:$AC\perp A^{\prime}B^{\prime}$
- 因为在$Rt\triangle ABC$中,$\angle ACB = 90^{\circ}$,$\angle A = 30^{\circ}$,所以$\angle B = 60^{\circ}$。
- 由旋转可知$CB = CB^{\prime}$,所以$\triangle BCB^{\prime}$是等边三角形,则$\angle BCB^{\prime}=60^{\circ}$。
- 那么$\angle A^{\prime}CA = 180^{\circ}-\angle BCB^{\prime}-\angle ACB = 180^{\circ}- 60^{\circ}-90^{\circ}=30^{\circ}$。
- 又因为$\angle A^{\prime}=\angle A = 30^{\circ}$,所以$\angle A^{\prime}FC = 180^{\circ}-\angle A^{\prime}-\angle A^{\prime}CA = 180^{\circ}-30^{\circ}-30^{\circ}=120^{\circ}$,$\angle AFC = 180^{\circ}-\angle A^{\prime}FC = 60^{\circ}$。
- 而$\angle A^{\prime}CA = 30^{\circ}$,所以$\angle A^{\prime}FC = 90^{\circ}$,即$AC\perp A^{\prime}B^{\prime}$。
【答案】:$AC\perp A^{\prime}B^{\prime}$
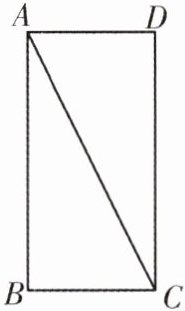
3. [变式]如图,四边形$ABCD$是矩形,$AC$为对角线.
(1)把$\triangle ABC$绕点$C$顺时针旋转一定角度$\alpha$得到$\triangle EFC$,点$A$的对应点$E$在$AD$的延长线上,点$B$的对应点为$F$,请你在图中作出$\triangle EFC$;(要求:尺规作图,不写作法,保留作图痕迹)
(2)在(1)的条件下,若$\angle CEF=26^{\circ}$,求旋转角$\alpha$的大小.
(1)把$\triangle ABC$绕点$C$顺时针旋转一定角度$\alpha$得到$\triangle EFC$,点$A$的对应点$E$在$AD$的延长线上,点$B$的对应点为$F$,请你在图中作出$\triangle EFC$;(要求:尺规作图,不写作法,保留作图痕迹)
(2)在(1)的条件下,若$\angle CEF=26^{\circ}$,求旋转角$\alpha$的大小.

答案:
【解析】:
(1) 以点$C$为圆心,$CB$长为半径画弧;再以点$E$为圆心,$AB$长为半径画弧,两弧交点即为点$F$,连接$CF$、$EF$,得到$\triangle EFC$。
(2) 因为四边形$ABCD$是矩形,所以$AD// BC$,$\angle B = 90^{\circ}$。
由旋转性质可知$\angle EFC=\angle B = 90^{\circ}$,$CE = CA$。
因为$AD// BC$,所以$\angle ECB=\angle AEC$。
又因为$CE = CA$,所以$\angle AEC=\angle EAC$。
在$\triangle EFC$中,$\angle CEF = 26^{\circ}$,$\angle EFC = 90^{\circ}$,则$\angle ECF=180^{\circ}-\angle EFC - \angle CEF=180^{\circ}-90^{\circ}-26^{\circ}=64^{\circ}$。
所以$\angle EAC=\angle AEC = 26^{\circ}$,那么$\angle ACB=\angle AEC = 26^{\circ}$。
所以旋转角$\alpha=\angle ECB=\angle ECF+\angle FCB$,$\angle FCB=\angle ACB = 26^{\circ}$,$\angle ECF = 64^{\circ}$,则$\alpha=64^{\circ}+26^{\circ}=52^{\circ}$。
【答案】:
(1) 作图见上述解析。
(2)$52^{\circ}$
(1) 以点$C$为圆心,$CB$长为半径画弧;再以点$E$为圆心,$AB$长为半径画弧,两弧交点即为点$F$,连接$CF$、$EF$,得到$\triangle EFC$。
(2) 因为四边形$ABCD$是矩形,所以$AD// BC$,$\angle B = 90^{\circ}$。
由旋转性质可知$\angle EFC=\angle B = 90^{\circ}$,$CE = CA$。
因为$AD// BC$,所以$\angle ECB=\angle AEC$。
又因为$CE = CA$,所以$\angle AEC=\angle EAC$。
在$\triangle EFC$中,$\angle CEF = 26^{\circ}$,$\angle EFC = 90^{\circ}$,则$\angle ECF=180^{\circ}-\angle EFC - \angle CEF=180^{\circ}-90^{\circ}-26^{\circ}=64^{\circ}$。
所以$\angle EAC=\angle AEC = 26^{\circ}$,那么$\angle ACB=\angle AEC = 26^{\circ}$。
所以旋转角$\alpha=\angle ECB=\angle ECF+\angle FCB$,$\angle FCB=\angle ACB = 26^{\circ}$,$\angle ECF = 64^{\circ}$,则$\alpha=64^{\circ}+26^{\circ}=52^{\circ}$。
【答案】:
(1) 作图见上述解析。
(2)$52^{\circ}$
查看更多完整答案,请扫码查看


