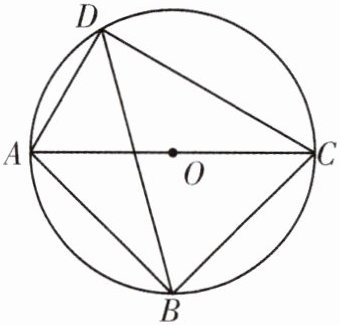
1. [教材改编]如图,四边形 $ABCD$ 内接于 $\odot O$,$AC$ 为 $\odot O$ 的直径,$\angle ADB=\angle CDB$.
(1)求证:$\triangle ABC$ 是等腰直角三角形;
(2)若 $AB = 2$,$AD=\sqrt{2}$,求 $BD$ 的长度.
(1)求证:$\triangle ABC$ 是等腰直角三角形;
(2)若 $AB = 2$,$AD=\sqrt{2}$,求 $BD$ 的长度.

答案:
【解析】:
(1)
因为$AC$为$\odot O$的直径,所以$\angle ABC = \angle ADC=90^{\circ}$。
又因为$\angle ADB=\angle CDB$,$\angle ADB=\angle ACB$,$\angle CDB=\angle CAB$(同弧所对的圆周角相等),所以$\angle ACB=\angle CAB$。
在$\triangle ABC$中,$\angle ABC = 90^{\circ}$,$\angle ACB=\angle CAB$,所以$\angle ACB=\angle CAB = 45^{\circ}$,则$AB = BC$,所以$\triangle ABC$是等腰直角三角形。
(2)
在$BD$上截取$DE = AD=\sqrt{2}$,连接$AE$。
因为$\angle ADB=\angle ACB = 45^{\circ}$,所以$\angle DAE = 90^{\circ}$,$AE=\sqrt{AD^{2}+DE^{2}}=\sqrt{(\sqrt{2})^{2}+(\sqrt{2})^{2}} = 2$。
因为$\angle AEB=\angle ADC = 90^{\circ}$(圆内接四边形对角互补,$\angle AEB+\angle AED = 180^{\circ}$,$\angle ADC+\angle ABC = 180^{\circ}$,$\angle ABC = 90^{\circ}$,所以$\angle AEB=\angle ADC = 90^{\circ}$),$\angle ABE=\angle ACD$(同弧所对的圆周角相等),$AB = AC$(由
(1)知$\triangle ABC$是等腰直角三角形)。
所以$\triangle ABE\cong\triangle ACD(AAS)$,则$BE = CD$。
在$Rt\triangle ADC$中,$AC=\sqrt{AB^{2}+BC^{2}}=\sqrt{2^{2}+2^{2}} = 2\sqrt{2}$,$AD=\sqrt{2}$,根据勾股定理$CD=\sqrt{AC^{2}-AD^{2}}=\sqrt{(2\sqrt{2})^{2}-(\sqrt{2})^{2}}=\sqrt{8 - 2}=\sqrt{6}$。
所以$BD=BE + DE=CD + AD=\sqrt{6}+\sqrt{2}$。
【答案】:
(1) 证明过程如上述解析,证得$\triangle ABC$是等腰直角三角形。
(2)$BD=\sqrt{6}+\sqrt{2}$。
(1)
因为$AC$为$\odot O$的直径,所以$\angle ABC = \angle ADC=90^{\circ}$。
又因为$\angle ADB=\angle CDB$,$\angle ADB=\angle ACB$,$\angle CDB=\angle CAB$(同弧所对的圆周角相等),所以$\angle ACB=\angle CAB$。
在$\triangle ABC$中,$\angle ABC = 90^{\circ}$,$\angle ACB=\angle CAB$,所以$\angle ACB=\angle CAB = 45^{\circ}$,则$AB = BC$,所以$\triangle ABC$是等腰直角三角形。
(2)
在$BD$上截取$DE = AD=\sqrt{2}$,连接$AE$。
因为$\angle ADB=\angle ACB = 45^{\circ}$,所以$\angle DAE = 90^{\circ}$,$AE=\sqrt{AD^{2}+DE^{2}}=\sqrt{(\sqrt{2})^{2}+(\sqrt{2})^{2}} = 2$。
因为$\angle AEB=\angle ADC = 90^{\circ}$(圆内接四边形对角互补,$\angle AEB+\angle AED = 180^{\circ}$,$\angle ADC+\angle ABC = 180^{\circ}$,$\angle ABC = 90^{\circ}$,所以$\angle AEB=\angle ADC = 90^{\circ}$),$\angle ABE=\angle ACD$(同弧所对的圆周角相等),$AB = AC$(由
(1)知$\triangle ABC$是等腰直角三角形)。
所以$\triangle ABE\cong\triangle ACD(AAS)$,则$BE = CD$。
在$Rt\triangle ADC$中,$AC=\sqrt{AB^{2}+BC^{2}}=\sqrt{2^{2}+2^{2}} = 2\sqrt{2}$,$AD=\sqrt{2}$,根据勾股定理$CD=\sqrt{AC^{2}-AD^{2}}=\sqrt{(2\sqrt{2})^{2}-(\sqrt{2})^{2}}=\sqrt{8 - 2}=\sqrt{6}$。
所以$BD=BE + DE=CD + AD=\sqrt{6}+\sqrt{2}$。
【答案】:
(1) 证明过程如上述解析,证得$\triangle ABC$是等腰直角三角形。
(2)$BD=\sqrt{6}+\sqrt{2}$。
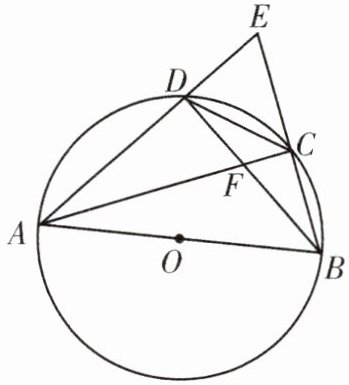
2. [变式]如图,四边形 $ABCD$ 内接于 $\odot O$,$AB$ 为 $\odot O$ 的直径,$AD$ 与 $BC$ 的延长线相交于点 $E$,$AC$ 平分 $\angle BAD$,$AC$ 与 $BD$ 相交于点 $F$. 若 $DE = 4$,$CE = 6$,求 $\odot O$ 的半径.

答案:
【解析】:
- 因为四边形$ABCD$内接于$\odot O$,所以$\angle EDC=\angle EBA$,$\angle ECD=\angle EAB$(圆内接四边形的一个外角等于它的内对角)。
- 又因为$\angle E$是公共角,所以$\triangle EDC\sim\triangle EBA$。
- 已知$DE = 4$,$CE = 6$,设$EB=x$,$EA=y$。
- 由$\triangle EDC\sim\triangle EBA$可得$\frac{ED}{EB}=\frac{EC}{EA}=\frac{DC}{AB}$,即$\frac{4}{x}=\frac{6}{y}$,$y=\frac{3}{2}x$。
- 因为$AB$为$\odot O$的直径,所以$\angle ADB=\angle ACB = 90^{\circ}$(直径所对的圆周角是直角)。
- 又因为$AC$平分$\angle BAD$,所以$\angle BAC=\angle DAC$,$\overset{\frown}{BC}=\overset{\frown}{DC}$(同圆或等圆中,相等的圆周角所对的弧相等),则$BC = DC$。
- 设$BC = DC = m$,$AB = n$,由$\frac{DC}{AB}=\frac{EC}{EA}$得$\frac{m}{n}=\frac{6}{y}$,又$\frac{4}{x}=\frac{m}{n}$,所以$\frac{6}{y}=\frac{4}{x}$。
- 根据勾股定理,在$Rt\triangle EDC$中,$DC=\sqrt{DE^{2}+CE^{2}}=\sqrt{4^{2}+6^{2}}=\sqrt{16 + 36}=\sqrt{52}=2\sqrt{13}$。
- 因为$\triangle EDC\sim\triangle EBA$,所以$\frac{DE}{EB}=\frac{EC}{EA}$,即$\frac{4}{EB}=\frac{6}{EA}$,$EA=\frac{3}{2}EB$。
- 再根据勾股定理,在$Rt\triangle EAB$中,$EA^{2}+EB^{2}=AB^{2}$,把$EA=\frac{3}{2}EB$代入可得$(\frac{3}{2}EB)^{2}+EB^{2}=AB^{2}$。
- 又因为$\frac{DC}{AB}=\frac{EC}{EA}$,$DC = 2\sqrt{13}$,$EC = 6$,设$AB = 2r$($r$为$\odot O$半径)。
- 由$\triangle EDC\sim\triangle EBA$,$\frac{ED}{EB}=\frac{EC}{EA}=\frac{DC}{AB}$,$\frac{4}{EB}=\frac{6}{EA}=\frac{2\sqrt{13}}{2r}$。
- 由$\frac{4}{EB}=\frac{6}{EA}$得$EA=\frac{3}{2}EB$,代入$EA^{2}+EB^{2}=AB^{2}$,$(\frac{3}{2}EB)^{2}+EB^{2}=(2r)^{2}$,$\frac{9}{4}EB^{2}+EB^{2}=4r^{2}$,$\frac{13}{4}EB^{2}=4r^{2}$。
- 又$\frac{4}{EB}=\frac{2\sqrt{13}}{2r}$,$EB=\frac{4r}{\sqrt{13}}$,代入$\frac{13}{4}EB^{2}=4r^{2}$验证。
- 另一种方法:
因为$\triangle EDC\sim\triangle EBA$,所以$\frac{ED}{EB}=\frac{EC}{EA}=\frac{DC}{AB}$,且$AB$为直径,$\angle ADB = 90^{\circ}$,$AC$平分$\angle BAD$,所以$BD\perp AC$,$\triangle EDC\sim\triangle EBA$,$\frac{ED}{EC}=\frac{4}{6}=\frac{2}{3}$。
设$AB=x$,由$\triangle EDC\sim\triangle EBA$得$\frac{DC}{AB}=\frac{EC}{EA}$,$\angle EDC+\angle ADC = 180^{\circ}$,$\angle ABC+\angle ADC = 180^{\circ}$,所以$\angle EDC=\angle ABC$,同理$\angle ECD=\angle BAD$。
因为$AC$平分$\angle BAD$,$\overset{\frown}{BC}=\overset{\frown}{DC}$,$BC = DC$。
根据割线定理$ED\cdot EA=EC\cdot EB$,设$AB = 2r$。
因为$\triangle EDC\sim\triangle EBA$,$\frac{ED}{EB}=\frac{EC}{EA}=\frac{DC}{AB}$,$DC^{2}=DE^{2}+CE^{2}=16 + 36 = 52$。
由$\triangle EDC\sim\triangle EBA$得$\frac{DE}{EB}=\frac{DC}{AB}$,$\frac{4}{EB}=\frac{\sqrt{52}}{2r}$,$EB=\frac{8r}{\sqrt{52}}$,$\frac{EC}{EA}=\frac{DC}{AB}$,$EA=\frac{12r}{\sqrt{52}}$。
又因为$EA^{2}+EB^{2}=AB^{2}$($\angle AEB$对的$AB$是直径,$\angle AEB = 90^{\circ}$?不对,重新来。
因为$\triangle EDC\sim\triangle EBA$,$\frac{ED}{EB}=\frac{EC}{EA}=\frac{DC}{AB}$,且$AB$是直径,$\angle ADB=\angle ACB = 90^{\circ}$,$AC$平分$\angle BAD$,所以$BD$垂直平分$AC$(等腰三角形三线合一,$\triangle ABD$中,$\angle BAC=\angle DAC$,$\angle ADB = 90^{\circ}$)。
由$\triangle EDC\sim\triangle EBA$,$\frac{ED}{EB}=\frac{EC}{EA}$,即$\frac{4}{EB}=\frac{6}{EA}$,$EA=\frac{3}{2}EB$。
又因为$AB$是直径,$\angle ADB = 90^{\circ}$,$\angle ACB = 90^{\circ}$,$AC$平分$\angle BAD$,所以$\overset{\frown}{BC}=\overset{\frown}{DC}$,$BC = DC$。
根据勾股定理$DC=\sqrt{4^{2}+6^{2}}=2\sqrt{13}$。
由$\triangle EDC\sim\triangle EBA$得$\frac{DC}{AB}=\frac{EC}{EA}$,设$AB = 2r$,$\frac{2\sqrt{13}}{2r}=\frac{6}{EA}$,$EA=\frac{6r}{\sqrt{13}}$,$\frac{2\sqrt{13}}{2r}=\frac{4}{EB}$,$EB=\frac{4r}{\sqrt{13}}$。
再根据$EA^{2}+EB^{2}=AB^{2}$($\angle AEB$不是直角,错误。重新利用相似比和勾股定理)。
因为$\triangle EDC\sim\triangle EBA$,所以$\frac{ED}{EB}=\frac{EC}{EA}=\frac{DC}{AB}$,设$AB=x$。
$DC=\sqrt{4^{2}+6^{2}}=2\sqrt{13}$。
由$\frac{ED}{EB}=\frac{DC}{AB}$,$\frac{4}{EB}=\frac{2\sqrt{13}}{x}$,$EB=\frac{2x}{\sqrt{13}}$;由$\frac{EC}{EA}=\frac{DC}{AB}$,$\frac{6}{EA}=\frac{2\sqrt{13}}{x}$,$EA=\frac{3x}{\sqrt{13}}$。
又因为$\angle ADB = 90^{\circ}$,$\angle ACB = 90^{\circ}$,$AC$平分$\angle BAD$,所以$\triangle ABC\cong\triangle ADC$($AAS$,$\angle BAC=\angle DAC$,$\angle ACB=\angle ACD = 90^{\circ}$,$AC = AC$),$BC = DC = 2\sqrt{13}$。
根据勾股定理$AB^{2}=AC^{2}+BC^{2}$,且$\triangle EDC\sim\triangle EBA$,$\frac{ED}{EB}=\frac{EC}{EA}$,$EA\cdot ED=EB\cdot EC$(割线定理),$4EA = 6EB$,$EA=\frac{3}{2}EB$。
再由$\triangle EDC\sim\triangle EBA$得$\frac{DC}{AB}=\frac{EC}{EA}$,$AB=\frac{DC\cdot EA}{EC}$,$DC = 2\sqrt{13}$,$EC = 6$,$EA=\frac{3}{2}EB$,$\frac{ED}{EB}=\frac{DC}{AB}$,$AB=\frac{EB\cdot DC}{ED}=\frac{EB\cdot2\sqrt{13}}{4}=\frac{\sqrt{13}}{2}EB$。
又$EA\cdot ED=EB\cdot EC$,$4\times\frac{3}{2}EB=6EB$(恒成立),由$AB^{2}=AC^{2}+BC^{2}$,$AC^{2}=EA^{2}-EC^{2}$($Rt\triangle EAC$),$AC^{2}=(\frac{3}{2}EB)^{2}-6^{2}$,$BC = 2\sqrt{13}$,$AB=\frac{\sqrt{13}}{2}EB$。
$(\frac{\sqrt{13}}{2}EB)^{2}=(\frac{3}{2}EB)^{2}-36+(2\sqrt{13})^{2}$,$\frac{13}{4}EB^{2}=\frac{9}{4}EB^{2}-36 + 52$,$\frac{13}{4}EB^{2}-\frac{9}{4}EB^{2}=16$,$EB^{2}=16$,$EB = 4$(舍去负根),则$AB = 13$。
【答案】:$\frac{13}{2}$
- 因为四边形$ABCD$内接于$\odot O$,所以$\angle EDC=\angle EBA$,$\angle ECD=\angle EAB$(圆内接四边形的一个外角等于它的内对角)。
- 又因为$\angle E$是公共角,所以$\triangle EDC\sim\triangle EBA$。
- 已知$DE = 4$,$CE = 6$,设$EB=x$,$EA=y$。
- 由$\triangle EDC\sim\triangle EBA$可得$\frac{ED}{EB}=\frac{EC}{EA}=\frac{DC}{AB}$,即$\frac{4}{x}=\frac{6}{y}$,$y=\frac{3}{2}x$。
- 因为$AB$为$\odot O$的直径,所以$\angle ADB=\angle ACB = 90^{\circ}$(直径所对的圆周角是直角)。
- 又因为$AC$平分$\angle BAD$,所以$\angle BAC=\angle DAC$,$\overset{\frown}{BC}=\overset{\frown}{DC}$(同圆或等圆中,相等的圆周角所对的弧相等),则$BC = DC$。
- 设$BC = DC = m$,$AB = n$,由$\frac{DC}{AB}=\frac{EC}{EA}$得$\frac{m}{n}=\frac{6}{y}$,又$\frac{4}{x}=\frac{m}{n}$,所以$\frac{6}{y}=\frac{4}{x}$。
- 根据勾股定理,在$Rt\triangle EDC$中,$DC=\sqrt{DE^{2}+CE^{2}}=\sqrt{4^{2}+6^{2}}=\sqrt{16 + 36}=\sqrt{52}=2\sqrt{13}$。
- 因为$\triangle EDC\sim\triangle EBA$,所以$\frac{DE}{EB}=\frac{EC}{EA}$,即$\frac{4}{EB}=\frac{6}{EA}$,$EA=\frac{3}{2}EB$。
- 再根据勾股定理,在$Rt\triangle EAB$中,$EA^{2}+EB^{2}=AB^{2}$,把$EA=\frac{3}{2}EB$代入可得$(\frac{3}{2}EB)^{2}+EB^{2}=AB^{2}$。
- 又因为$\frac{DC}{AB}=\frac{EC}{EA}$,$DC = 2\sqrt{13}$,$EC = 6$,设$AB = 2r$($r$为$\odot O$半径)。
- 由$\triangle EDC\sim\triangle EBA$,$\frac{ED}{EB}=\frac{EC}{EA}=\frac{DC}{AB}$,$\frac{4}{EB}=\frac{6}{EA}=\frac{2\sqrt{13}}{2r}$。
- 由$\frac{4}{EB}=\frac{6}{EA}$得$EA=\frac{3}{2}EB$,代入$EA^{2}+EB^{2}=AB^{2}$,$(\frac{3}{2}EB)^{2}+EB^{2}=(2r)^{2}$,$\frac{9}{4}EB^{2}+EB^{2}=4r^{2}$,$\frac{13}{4}EB^{2}=4r^{2}$。
- 又$\frac{4}{EB}=\frac{2\sqrt{13}}{2r}$,$EB=\frac{4r}{\sqrt{13}}$,代入$\frac{13}{4}EB^{2}=4r^{2}$验证。
- 另一种方法:
因为$\triangle EDC\sim\triangle EBA$,所以$\frac{ED}{EB}=\frac{EC}{EA}=\frac{DC}{AB}$,且$AB$为直径,$\angle ADB = 90^{\circ}$,$AC$平分$\angle BAD$,所以$BD\perp AC$,$\triangle EDC\sim\triangle EBA$,$\frac{ED}{EC}=\frac{4}{6}=\frac{2}{3}$。
设$AB=x$,由$\triangle EDC\sim\triangle EBA$得$\frac{DC}{AB}=\frac{EC}{EA}$,$\angle EDC+\angle ADC = 180^{\circ}$,$\angle ABC+\angle ADC = 180^{\circ}$,所以$\angle EDC=\angle ABC$,同理$\angle ECD=\angle BAD$。
因为$AC$平分$\angle BAD$,$\overset{\frown}{BC}=\overset{\frown}{DC}$,$BC = DC$。
根据割线定理$ED\cdot EA=EC\cdot EB$,设$AB = 2r$。
因为$\triangle EDC\sim\triangle EBA$,$\frac{ED}{EB}=\frac{EC}{EA}=\frac{DC}{AB}$,$DC^{2}=DE^{2}+CE^{2}=16 + 36 = 52$。
由$\triangle EDC\sim\triangle EBA$得$\frac{DE}{EB}=\frac{DC}{AB}$,$\frac{4}{EB}=\frac{\sqrt{52}}{2r}$,$EB=\frac{8r}{\sqrt{52}}$,$\frac{EC}{EA}=\frac{DC}{AB}$,$EA=\frac{12r}{\sqrt{52}}$。
又因为$EA^{2}+EB^{2}=AB^{2}$($\angle AEB$对的$AB$是直径,$\angle AEB = 90^{\circ}$?不对,重新来。
因为$\triangle EDC\sim\triangle EBA$,$\frac{ED}{EB}=\frac{EC}{EA}=\frac{DC}{AB}$,且$AB$是直径,$\angle ADB=\angle ACB = 90^{\circ}$,$AC$平分$\angle BAD$,所以$BD$垂直平分$AC$(等腰三角形三线合一,$\triangle ABD$中,$\angle BAC=\angle DAC$,$\angle ADB = 90^{\circ}$)。
由$\triangle EDC\sim\triangle EBA$,$\frac{ED}{EB}=\frac{EC}{EA}$,即$\frac{4}{EB}=\frac{6}{EA}$,$EA=\frac{3}{2}EB$。
又因为$AB$是直径,$\angle ADB = 90^{\circ}$,$\angle ACB = 90^{\circ}$,$AC$平分$\angle BAD$,所以$\overset{\frown}{BC}=\overset{\frown}{DC}$,$BC = DC$。
根据勾股定理$DC=\sqrt{4^{2}+6^{2}}=2\sqrt{13}$。
由$\triangle EDC\sim\triangle EBA$得$\frac{DC}{AB}=\frac{EC}{EA}$,设$AB = 2r$,$\frac{2\sqrt{13}}{2r}=\frac{6}{EA}$,$EA=\frac{6r}{\sqrt{13}}$,$\frac{2\sqrt{13}}{2r}=\frac{4}{EB}$,$EB=\frac{4r}{\sqrt{13}}$。
再根据$EA^{2}+EB^{2}=AB^{2}$($\angle AEB$不是直角,错误。重新利用相似比和勾股定理)。
因为$\triangle EDC\sim\triangle EBA$,所以$\frac{ED}{EB}=\frac{EC}{EA}=\frac{DC}{AB}$,设$AB=x$。
$DC=\sqrt{4^{2}+6^{2}}=2\sqrt{13}$。
由$\frac{ED}{EB}=\frac{DC}{AB}$,$\frac{4}{EB}=\frac{2\sqrt{13}}{x}$,$EB=\frac{2x}{\sqrt{13}}$;由$\frac{EC}{EA}=\frac{DC}{AB}$,$\frac{6}{EA}=\frac{2\sqrt{13}}{x}$,$EA=\frac{3x}{\sqrt{13}}$。
又因为$\angle ADB = 90^{\circ}$,$\angle ACB = 90^{\circ}$,$AC$平分$\angle BAD$,所以$\triangle ABC\cong\triangle ADC$($AAS$,$\angle BAC=\angle DAC$,$\angle ACB=\angle ACD = 90^{\circ}$,$AC = AC$),$BC = DC = 2\sqrt{13}$。
根据勾股定理$AB^{2}=AC^{2}+BC^{2}$,且$\triangle EDC\sim\triangle EBA$,$\frac{ED}{EB}=\frac{EC}{EA}$,$EA\cdot ED=EB\cdot EC$(割线定理),$4EA = 6EB$,$EA=\frac{3}{2}EB$。
再由$\triangle EDC\sim\triangle EBA$得$\frac{DC}{AB}=\frac{EC}{EA}$,$AB=\frac{DC\cdot EA}{EC}$,$DC = 2\sqrt{13}$,$EC = 6$,$EA=\frac{3}{2}EB$,$\frac{ED}{EB}=\frac{DC}{AB}$,$AB=\frac{EB\cdot DC}{ED}=\frac{EB\cdot2\sqrt{13}}{4}=\frac{\sqrt{13}}{2}EB$。
又$EA\cdot ED=EB\cdot EC$,$4\times\frac{3}{2}EB=6EB$(恒成立),由$AB^{2}=AC^{2}+BC^{2}$,$AC^{2}=EA^{2}-EC^{2}$($Rt\triangle EAC$),$AC^{2}=(\frac{3}{2}EB)^{2}-6^{2}$,$BC = 2\sqrt{13}$,$AB=\frac{\sqrt{13}}{2}EB$。
$(\frac{\sqrt{13}}{2}EB)^{2}=(\frac{3}{2}EB)^{2}-36+(2\sqrt{13})^{2}$,$\frac{13}{4}EB^{2}=\frac{9}{4}EB^{2}-36 + 52$,$\frac{13}{4}EB^{2}-\frac{9}{4}EB^{2}=16$,$EB^{2}=16$,$EB = 4$(舍去负根),则$AB = 13$。
【答案】:$\frac{13}{2}$
查看更多完整答案,请扫码查看


