11. (14分)如图,点$A$在直线$l$外. 用两种不同的方法作$\odot O$,使$\odot O$过$A$点,且与直线$l$相切.
(要求:尺规作图,不写作法,保留作图痕迹)

(要求:尺规作图,不写作法,保留作图痕迹)

答案:
【解析】:
方法一:
1. 过点$A$作直线$l$的垂线$AB$,垂足为$B$。
2. 作线段$AB$的垂直平分线$m$。
3. 在直线$m$上取一点$O_1$($O_1$不与$AB$中点重合),以$O_1$为圆心,$O_1A$(或$O_1B$)为半径作圆$\odot O_1$,则$\odot O_1$过$A$点且与直线$l$相切。
方法二:
1. 作一个与直线$l$相切的辅助圆$\odot C$(任意作一个与$l$相切的圆即可)。
2. 连接$AC$,作$AC$的垂直平分线$n$,交$AC$于点$D$。
3. 过点$D$作直线$l$的平行线$p$,交$\odot C$于点$O_2$(取其中一个交点)。
4. 以$O_2$为圆心,$O_2A$为半径作圆$\odot O_2$,则$\odot O_2$过$A$点且与直线$l$相切。
【答案】:作出符合要求的两个圆(根据上述方法作出的两个圆,保留作图痕迹)。
方法一:
1. 过点$A$作直线$l$的垂线$AB$,垂足为$B$。
2. 作线段$AB$的垂直平分线$m$。
3. 在直线$m$上取一点$O_1$($O_1$不与$AB$中点重合),以$O_1$为圆心,$O_1A$(或$O_1B$)为半径作圆$\odot O_1$,则$\odot O_1$过$A$点且与直线$l$相切。
方法二:
1. 作一个与直线$l$相切的辅助圆$\odot C$(任意作一个与$l$相切的圆即可)。
2. 连接$AC$,作$AC$的垂直平分线$n$,交$AC$于点$D$。
3. 过点$D$作直线$l$的平行线$p$,交$\odot C$于点$O_2$(取其中一个交点)。
4. 以$O_2$为圆心,$O_2A$为半径作圆$\odot O_2$,则$\odot O_2$过$A$点且与直线$l$相切。
【答案】:作出符合要求的两个圆(根据上述方法作出的两个圆,保留作图痕迹)。
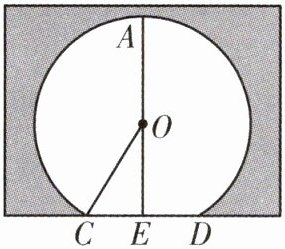
12. (10分)福州是一座蕴存着绚丽风光,并拥有深厚人文底蕴的城市. 它散落分布着很多历史悠久的古村落. 现福州某乡镇景区需要复原一个古代圆拱形木门(示意图),已知木门半径$OC=5m$,测得门槛$CD=6m$,门的高$AE\perp CD$于点$E$,且$AE$过点$O$,求$AE$的长.

答案:
【解析】:
因为$AE\perp CD$,$AE$过圆心$O$,$CD = 6m$,根据垂径定理可知$CE=\frac{1}{2}CD=\frac{1}{2}\times6 = 3m$。
在$Rt\triangle OCE$中,已知$OC = 5m$,$CE = 3m$,根据勾股定理$a^{2}+b^{2}=c^{2}$(其中$c$为斜边,$a$、$b$为两直角边),可得$OE=\sqrt{OC^{2}-CE^{2}}=\sqrt{5^{2}-3^{2}}=\sqrt{25 - 9}=\sqrt{16}=4m$。
又因为$OA=OC = 5m$,所以$AE=OA + OE=5 + 4=9m$。
【答案】:$9m$
因为$AE\perp CD$,$AE$过圆心$O$,$CD = 6m$,根据垂径定理可知$CE=\frac{1}{2}CD=\frac{1}{2}\times6 = 3m$。
在$Rt\triangle OCE$中,已知$OC = 5m$,$CE = 3m$,根据勾股定理$a^{2}+b^{2}=c^{2}$(其中$c$为斜边,$a$、$b$为两直角边),可得$OE=\sqrt{OC^{2}-CE^{2}}=\sqrt{5^{2}-3^{2}}=\sqrt{25 - 9}=\sqrt{16}=4m$。
又因为$OA=OC = 5m$,所以$AE=OA + OE=5 + 4=9m$。
【答案】:$9m$
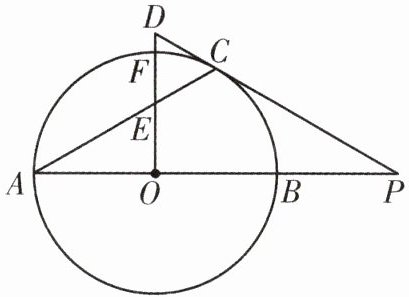
13. (16分)如图,$AB$为$\odot O$的直径,点$C$,$F$在半圆上,过点$C$的直线与$OF$的延长线相交于点$D$,与$AB$的延长线相交于点$P$,$AC$与$OF$相交于点$E$,$DC=DE$,$OD\perp AB$.
(1)求证:$PC$为$\odot O$的切线;
(2)若$OB=BP$,$AB=4$,求点$C$到$AP$的距离.
(1)求证:$PC$为$\odot O$的切线;
(2)若$OB=BP$,$AB=4$,求点$C$到$AP$的距离.

答案:
【解析】:
### $(1)$ 证明$PC$为$\odot O$的切线
连接$OC$。
因为$OA = OC$,所以$\angle OAC=\angle OCA$。
因为$OD\perp AB$,所以$\angle AOE = 90^{\circ}$,则$\angle OEA+\angle OAC = 90^{\circ}$。
又因为$DC = DE$,所以$\angle DCE=\angle DEC$。
而$\angle DEC=\angle OEA$(对顶角相等),所以$\angle DCE=\angle OEA$。
那么$\angle DCE+\angle OCA=\angle OEA+\angle OAC = 90^{\circ}$,即$\angle DCO = 90^{\circ}$。
因为$OC$是$\odot O$的半径,且$OC\perp DC$,所以$PC$为$\odot O$的切线。
### $(2)$ 求点$C$到$AP$的距离
已知$AB = 4$,则$OB=OC = 2$。
因为$OB = BP$,所以$OP=OB + BP=4$。
在$Rt\triangle OCP$中,$\sin P=\frac{OC}{OP}=\frac{2}{4}=\frac{1}{2}$,所以$\angle P = 30^{\circ}$。
因为$OD\perp AB$,$PC$为切线,$\angle DCO = 90^{\circ}$,$\angle P = 30^{\circ}$,所以$\angle COB = 60^{\circ}$。
过点$C$作$CH\perp AB$于点$H$。
在$Rt\triangle OCH$中,$\angle COH = 60^{\circ}$,$OC = 2$,则$\sin\angle COH=\frac{CH}{OC}$。
所以$CH = OC\cdot\sin60^{\circ}=2\times\frac{\sqrt{3}}{2}=\sqrt{3}$,即点$C$到$AP$的距离为$\sqrt{3}$。
【答案】:
$(1)$ 证明如上;$(2)$$\boldsymbol{\sqrt{3}}$
### $(1)$ 证明$PC$为$\odot O$的切线
连接$OC$。
因为$OA = OC$,所以$\angle OAC=\angle OCA$。
因为$OD\perp AB$,所以$\angle AOE = 90^{\circ}$,则$\angle OEA+\angle OAC = 90^{\circ}$。
又因为$DC = DE$,所以$\angle DCE=\angle DEC$。
而$\angle DEC=\angle OEA$(对顶角相等),所以$\angle DCE=\angle OEA$。
那么$\angle DCE+\angle OCA=\angle OEA+\angle OAC = 90^{\circ}$,即$\angle DCO = 90^{\circ}$。
因为$OC$是$\odot O$的半径,且$OC\perp DC$,所以$PC$为$\odot O$的切线。
### $(2)$ 求点$C$到$AP$的距离
已知$AB = 4$,则$OB=OC = 2$。
因为$OB = BP$,所以$OP=OB + BP=4$。
在$Rt\triangle OCP$中,$\sin P=\frac{OC}{OP}=\frac{2}{4}=\frac{1}{2}$,所以$\angle P = 30^{\circ}$。
因为$OD\perp AB$,$PC$为切线,$\angle DCO = 90^{\circ}$,$\angle P = 30^{\circ}$,所以$\angle COB = 60^{\circ}$。
过点$C$作$CH\perp AB$于点$H$。
在$Rt\triangle OCH$中,$\angle COH = 60^{\circ}$,$OC = 2$,则$\sin\angle COH=\frac{CH}{OC}$。
所以$CH = OC\cdot\sin60^{\circ}=2\times\frac{\sqrt{3}}{2}=\sqrt{3}$,即点$C$到$AP$的距离为$\sqrt{3}$。
【答案】:
$(1)$ 证明如上;$(2)$$\boldsymbol{\sqrt{3}}$
查看更多完整答案,请扫码查看


