《2024年绿色通道45分钟课时作业与单元测评数学选择性必修第二册》

10. 已知函数$f(x)=\frac{\ln x}{x}$．
(1)求函数$f(x)$的导数；
(2)求函数$f(x)$的单调区间.

答案： 10.解　
(1)函数f(x)=$\frac{1nx}{x}$的定义域为(0,十∞∞),f′(x)=$\frac{1−lnx}{x²}$.
(2)当f'(x)＞0,即0＜r＜e时,函数f(x)单调递增;当f'(x)＜0,即x＞e时,函数f(x)单调递减,故函数f(x)的单调递增区间为(0,e),单调递减区间为(e,+oo).

11.（多选）下列函数在定义域上为增函数的有（ ）
A. $f(x)=2x^{4}$
B. $f(x)=x\mathrm{e}^{2x}$
C. $f(x)=x-\cos x$
D. $f(x)=\mathrm{e}^{x}-\mathrm{e}^{-x}-2x$

答案： 11.CD　函数f(x)=2x⁴的定义域为R,其导数f'(x)=8,x³,当x＜0时,f'(x)＜0,当x＞0时,f'(x)＞0,所以f(x)在定义域R上不是增函数;函数f(x)=xe²的定义域为R,其导数∮'(x)=(2x+1)e²,当x＜−$\frac{1}{2}$时,f'(x)＜0,当x＞−$\frac{1}{2}$时,f'(x)＞0,所以∮(x)在定义域R上不是增函数;函数∮(x)=x−cosx的定义域为R,其导数∮'(x)=1+sinx≥0,所以f(x)在定义域R上是增函数;函数f(x)=e²一ex−2x的定义域为R,其导数f'(x)=e²+e−x−2≥2　$\sqrt{e.e−x}$−2=0,当且仅当ex=ex,即x=0時,等号成立,所以f(x)在定义域R 上是增函数.故选CD.

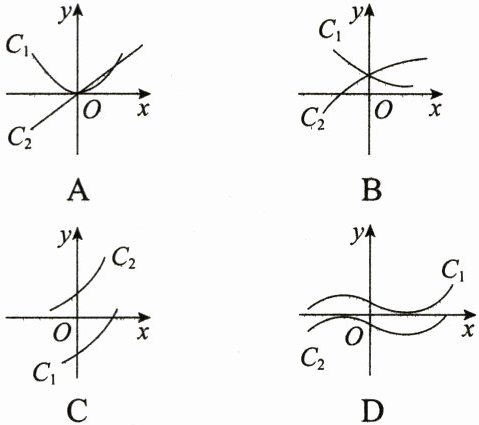
12.（多选）设$f'(x)$是函数$f(x)$的导函数，将$y = f(x)$和$y = f'(x)$的图象画在同一个直角坐标系中，正确的是（ ）

答案： 12.ABC　A、B、C均有可能;对于D,若C1为导函数图象，则y=f(x)应为增函数,不符合;若C2为导函数图象,则y=f(x)应为减函数，也不符合.故选ABC.

13. 已知函数$f(x)=k\mathrm{e}^{x - 1}-x+\frac{1}{2}x^{2}$（$k$为常数），曲线$y = f(x)$在点$(0,f(0))$处的切线与$x$轴平行，则$f(x)$的单调递增区间为______．

答案： 13.(0,+o∞)解析　由题知,∮'(x)=kex−¹−1+x,因为曲线y=f(x)在点(0,f
(0))处的切线与x轴平行,所以f'
(0)=k.e−¹−1=0,解得k=e,故f'(x)=e²+x−1.令f'(x)＞0,解得x＞0,故f(x)的单调递增区间为(0,+∞∞).

14. 在①$l_{2}// l_{1}$，②$l_{2}\perp l_{1}$，③$l_{2}$与坐标轴围成的三角形的面积为$\frac{1}{2}$这三个条件中任选一个，补充在下面问题中，并解答.
问题：已知函数$f(x)=\ln x - 2mx$，直线$l_{1}:x + y - 1 = 0$，函数$f(x)$的图象在点$(1,f(1))$处的切线为$l_{2}$，且______.
(1)求实数$m$的值；
(2)判断$f(x)=\ln x - 2mx$的单调性.

答案： 14.解　若选条件①.
(1)
∵直线l:x+y−1=0的斜率为−1,l2//l1,
∴切线l2的斜率为−1,又f'(x)=$\frac{1}{x}$−2m,
∴f'
(1)　11　2m=−1,
∴m=1.
(2)由
(1)知f(x)=1nx−2x,其定义域为(0,+oo),f'(x)=$\frac{1}{x}$−2.令f,(x)＞0,得0＜x＜$\frac{1}{2}$;令f'(x)＜0,得x＞$\frac{1}{2}$
∴f(x)=1nx−2x在(0,$\frac{1}{2}$)上单调递增,在($\frac{1}{2}$,+∞)上单调递减.
若选条件②.
(1)
∵直线l1:x+y−1=0的斜率为−1,l2⊥l1,
∴切线L2的斜率为1,又f'(x)=$\frac{1}{x}$−2m,
∴f'
(1)=11　2m=1,
∴m=0.
(2)由
(1)知f(x)=1nx,其定义域为(0,+oo),
∴∮'(x)=$\frac{1}{x}$＞0在(0,+∞)上恒成立,
∴f(x)=1nx在(0,+oo)上单调递增,
若选条件③.
(1)
∵∮'(x)=$\frac{1}{x}$−2m,f
(1)=−2m,
∴切点坐标为(1,−2m),切线l2的斜率k=f'
(1)=1−2m,
∴切线l2的方程为y+2m=(1−2m)(x−1).令x=0,得y=−1;令y=0,得x=$\frac{1}{1−2m}$,则$\frac{1}{2}$×|−1|×|$\frac{1}{1−2m}$|=$\frac{1}{2}$,得m=1或m=0.
(2)由
(1)知当m=1时,f(x)=1nx−2x,其定义域为(0,+oo),f'(x)=$\frac{1}{x}$−2.令∮'(x)＞0,得0＜x＜$\frac{1}{2}$;令∮'(x)＜0,得x＞$\frac{1}{2}$
∴f(x)=1nx−2x在(0,$\frac{1}{2}$)上单调递增，在($\frac{1}{2}$,+∞)上单调递减.当m=0时,f(x)=lnx,其定义域为(0,+oo),
∴∮'(x)=$\frac{1}{x}$＞0在(0,+∞o)上恒成立，
∴f(x)=lnx在(0,+oo)上单调递增.

15.（新定义题）若函数$y = f(x)$在区间$D$上单调递增，且函数$y = f'(x)$在区间$D$上也单调递增（其中$f'(x)$是函数$f(x)$的导函数），那么称函数$y = f(x)$是区间$D$上的“快增函数”，区间$D$叫做“快增区间”，则函数$f(x)=\sin^{2}x + 2\sin x$（$x\in[0,\pi]$）的“快增区间”为______．

答案： 15.[0,$\frac{π}{6}$解析　由题知f'(x)=2sinxcosx+2cosx=2cosx(sinx+1).因为sinx+1≥0恒成立,当x∈{0,$\frac{π}{2}$]时,cosx≥0,所以f,(x)≥0,即f(x))单调递增;当x∈($\frac{π}{2}$,π]时,cosz＜0,所以∮"(x)＜0,即f(x)单调递减.令g(x)=J"(x)=²2sinxcosx+2cosx,x∈[[0 $\frac{π}{2}$],则g’(x)=2cos²²x−2sin²²x−2sinxx=2²−4Ssin²x−2sinx,令t=sinx,则t∈[0,1],令h(t)=−4t²−2t+2=−2(2t−1)(±+1)(t∈[0,1]),所以当t∈[0,$\frac{1}{2}$时,h(t)≥0,即当x∈[0,$\frac{π}{6}$]时,g,(x)≥0,g(z)单调递增,所以函数f(x)=sin²x+2sinx(x∈[0,π])的“快增区间”为[0,$\frac{π}{6}$1.

16.（逻辑推理）写出一个同时具有下列性质①②③的函数$f(x)=$______．
①$f(x_{1})f(x_{2})=f(x_{1}+x_{2})$；②$f'(x)＞0$；③$f'(x)＞f(x)$．

答案： 16.e²(答案不唯一)解析　由①知函数f(x)可以是指数函数,由②可知函数f(x)单调递增.设f(x)=a²(a＞1),由f'(x)=ax1na＞a²,得a＞e.满足题意的函数可以为∮(x)=e²x.