《2024年绿色通道45分钟课时作业与单元测评数学选择性必修第二册》

1. 设函数$f(x)$的图象如图所示，则导函数$f'(x)$的图象可能为（ ）

答案： 1.C　因为f(x)在(一co,1),(4,十oo)上是减函数,在(1,4)上是增函数,所以当x＜1或x＞4时,f'(x)＜0;当1＜x＜4时,f'(x)＞0.故选C.

2. 函数$f(x)=-x^{3}+x$在$(1,+\infty)$内为（ ）
A. 减函数
B. 增函数
C. 常数函数
D. 不能确定

答案： 2.A　当x∈(1,+oo)时,f'(x)=−3x²+1＜0,故f(x)在(1,十oo)内为减函数.

3. 函数$f(x)=x^{2}+\ln x$（ ）
A. 在$(0,+\infty)$上单调递增
B. 在$(0,+\infty)$上单调递减
C. 在$(0,1)$上单调递减，在$(1,+\infty)$上单调递增
D. 在$(0,1)$上单调递增，在$(1,+\infty)$上单调递减

答案： 3.Af'(x)=2x+$\frac{1}{x}$(x＞0),因为当x＞0时,f'(x)＞0 恒成立,所以f(x)在(0,十oo)上单调递增，故选A.

4. 函数$f(x)=3+x\ln x$的单调递增区间是（ ）
A. $(0,\frac{1}{\mathrm{e}})$
B. $(\mathrm{e},+\infty)$
C. $(\frac{1}{\mathrm{e}},+\infty)$
D. $(\frac{1}{\mathrm{e}},\mathrm{e})$

答案： 4.Cf'(x)=1nx+1(x＞0),令f′(x)＞0,即1nx+1＞0,得x＞$\frac{1}{e}$,故函数f(x)的单调递增区间为($\frac{1}{e}$,+∞).故选C.

5. 下列函数中，在$(0,+\infty)$上单调递增的是（ ）
A. $y = \sin x$
B. $y = x\mathrm{e}^{x}$
C. $y = x^{3}-x$
D. $y = \ln x - x$

答案： 5.BA中,y'=cosx,当x＞0时,y'的符号不确定;B中,y=e²+xe²=(x+1)e²,当x＞0时,y'＞0,故在(0,+∞o)上单调递增;C中,y'=3x²−1,当x＞0时,y'＞−1,单调性不确定;D中,y'=$\frac{1}{x}$−1,当x＞0时,y,＞−1,单调性不确定.故选B.

6.（多选）如图所示是函数$y = f(x)$的导函数$f'(x)$的图象，则下列判断正确的是（ ）

A. $f(x)$在$(-2,1)$上单调递增
B. $f(x)$在$(1,2)$上单调递增
C. $f(x)$在$(4,5)$上单调递增
D. $f(x)$在$(-3,-2)$上单调递增

答案： 6.BC　由题图知当x∈(−1,2)U(4,5)时,f'(x)＞0,所以在(−1,2),(4,5)上,f(x)单调递增,故A错误,B、C 正确;当x∈(−3,−2)时,∮'(x)＜0,所以在(−3,−2)上,f(x)单调递减，故D错误,

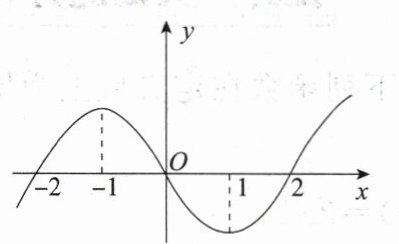
7. 已知$f(x)$在$\mathbf{R}$上是可导函数，$f(x)$的图象如图所示，则不等式$f'(x)＞0$的解集为______

答案： 7.(−∞0,−1)U(1,+∞)解析　由f(x)的图象知,函数f(x)在(一oo,−1)上单调递增，在(−1,1)上单调递减,在(1,+oo)上单调递增,所以f'(x)＞0的解集为(−∞∞,−1)U(1,+∞∞).

8. 函数$f(x)=x + 2\cos x$，$x\in(0,\pi)$的单调递减区间是______．

答案： 8.($\frac{π}{6}$,))解析　由f'(x)=1−2sinx＜0,得sinx＞$\frac{1}{2}$,又x∈(0,,π),所以x∈($\frac{π}{6}$).

9. 证明：函数$f(x)=x+\frac{4}{x}$在$(0,2)$上单调递减，在$(2,+\infty)$上单调递增.

答案： 9.证明　因为f'(x)=1−$\frac{4}{x²}$,当x∈(0,2)时,0＜x²＜4,所以1−$\frac{4}{x²}$＜0,所以f(x)在(0,2)上单调递减;当x∈(2,+∞0)时,x²＞4,所以1−$\frac{4}{x²}$＞0,所以f(x)在(2,+∞o)上单调递增.