《2024年绿色通道45分钟课时作业与单元测评数学选择性必修第二册》

1. 设$a_{n}=\frac{1}{n}+\frac{1}{n + 1}+\frac{1}{n + 2}+\frac{1}{n + 3}+\cdots+\frac{1}{n^{2}},n\in\mathbf{N}^{*}$，则$a_{2}=$（ ）
A. $\frac{1}{4}$
B. $\frac{1}{2}+\frac{1}{3}$
C. $\frac{1}{2}+\frac{1}{3}+\frac{1}{4}$
D. $\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{5}$

答案： C
∵$a_{n}=\frac{1}{n}+\frac{1}{n + 1}+\frac{1}{n + 2}+\frac{1}{n + 3}+\cdots+\frac{1}{n^{2}},n\in\mathbf{N}^{*}$，
∴$a_{2}=\frac{1}{2}+\frac{1}{3}+\frac{1}{4}$. 故选C.

2. 在数列$\{a_{n}\}$中，$a_{n}=\frac{n + 2}{n + 1}$，则$\{a_{n}\}$（ ）
A. 是常数列
B. 是摆动数列
C. 是递增数列
D. 是递减数列

答案： D 在数列$\{a_{n}\}$中，$a_{n}=\frac{n + 2}{n + 1}=1+\frac{1}{n + 1}$，由反比例函数的性质知$\{a_{n}\}$在$n\in\mathbf{N}^{*}$时是递减数列，故选D.

3. 已知某报告厅共有15排，共390个座位，并且从第二排起，每排比前一排多2个座位，则最后一排的座位数为（ ）
A. 12
B. 26
C. 40
D. 50

答案： C 根据题意，各排座位数可看作等差数列$\{a_{n}\}$，设其公差为$d$，前$n$项和为$S_{n}$，则$d = 2$，$S_{15}=15a_{1}+\frac{15\times14}{2}\times2=15a_{1}+15\times14 = 390$，所以$a_{1}=12$，即得$a_{15}=a_{1}+14d=12 + 14\times2 = 40$，故选C.

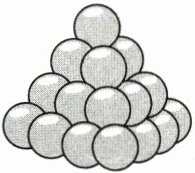
4. 宋代制酒业很发达，为了存储方便，酒缸是要一层一层堆起来的，形成堆垛，用简便的方法算出堆垛中酒缸的总数，古代称之为堆垛术. 有这么一道关于“堆垛”求和的问题：将半径相等的圆球堆成一个三角垛，如图，底层是每边为$n$个圆球的三角形，向上逐层每边减少一个圆球，顶层为一个圆球，我们发现，当$n = 1,2,3,4$时，圆球总个数分别为1，4，10，20，则当$n = 5$时，圆球总个数为（ ）

A. 30
B. 35
C. 40
D. 45

答案： B 当$n = 1,2,3,4$时，圆球总个数分别为$1,4,10,20$，所以当$n = 4$时，从上到下每层圆球的个数分别为$1,3 = 1 + 2,6 = 1 + 2 + 3,10 = 1 + 2 + 3 + 4$，可得当$n = 5$时，底层圆球的个数为$1 + 2 + 3 + 4 + 5 = 15$，故一共有$20+15 = 35$个圆球. 故选B.

5. 已知等差数列$\{a_{n}\}$的前$n$项和为$S_{n}$，且$S_{2}=4$，$S_{4}=16$，数列$\{b_{n}\}$满足$b_{n}=a_{n}+a_{n + 1}$，则数列$\{b_{n}\}$的前9项和$T_{9}=$（ ）

A. 20
B. 80
C. 166
D. 180

答案： D 设等差数列$\{a_{n}\}$的公差为$d$. 由等差数列$\{a_{n}\}$的前$n$项和为$S_{n}$，且$S_{2}=4$，$S_{4}=16$，可得$\begin{cases}2a_{1}+d = 4\\4a_{1}+6d = 16\end{cases}$，解得$\begin{cases}d = 2\\a_{1}=1\end{cases}$.$\therefore a_{n}=2n - 1$，$\therefore b_{n}=a_{n}+a_{n + 1}=4n$，$\therefore$数列$\{b_{n}\}$的前$9$项和$T_{9}=\frac{9\times(b_{1}+b_{9})}{2}=180$.

6. 已知三角形数表：
现把数表按从上到下、从左到右的顺序展开为数列$\{a_{n}\}$，则$a_{1000}=$（ ）
A. $3^{7}$
B. $3^{8}$
C. $3^{9}$
D. $3^{10}$

答案： B 第一行有$1$个数，第二行有$2$个数，$\cdots$，第$n$行有$n$个数，所以$\frac{n(1 + n)}{2}\leq100$中，$n$的最大值是$13$，前$13$行共有$\frac{13\times(1 + 13)}{2}=91$个数，第$100$个数是第$14$行的第$9$个数，根据题意可知，第$9$个数是$3^{9 - 1}=3^{8}$，即$a_{100}=3^{8}$. 故选B.

7. （2023·沈阳东北育才学校期末）若等差数列$\{a_{n}\}$的公差为$d$，前$n$项和为$S_{n}$，记$b_{n}=\frac{S_{n}}{n}$，则（ ）
A. 数列$\{b_{n}\}$是公差为$d$的等差数列
B. 数列$\{b_{n}\}$是公差为$2d$的等差数列
C. 数列$\{a_{n}+b_{n}\}$是公差为$\frac{3}{2}d$的等差数列
D. 数列$\{a_{n}-b_{n}\}$是公差为$\frac{3}{2}d$的等差数列

答案： C 根据题意，得$a_{n}=a_{1}+(n - 1)d$，$S_{n}=na_{1}+\frac{n(n - 1)}{2}\cdot d$，则$b_{n}=\frac{S_{n}}{n}=\frac{1}{2}dn+a_{1}-\frac{1}{2}d$对应的函数是一次函数，所以数列$\{b_{n}\}$是公差为$\frac{1}{2}d$的等差数列，故选项A、B错误；由$a_{n}+b_{n}=\frac{3}{2}dn+2a_{1}-\frac{3}{2}d$对应的函数是一次函数，得数列$\{a_{n}+b_{n}\}$是公差为$\frac{3}{2}d$的等差数列，故选项C正确；由$a_{n}-b_{n}=\frac{1}{2}dn-\frac{1}{2}d$对应的函数是一次函数，得数列$\{a_{n}-b_{n}\}$是公差为$\frac{1}{2}d$的等差数列，故选项D错误.

8. （多选）（2024·福建龙岩连城一中月考）已知两个等差数列$\{a_{n}\}$和$\{b_{n}\}$的前$n$项和分别为$S_{n}$和$T_{n}$，且$\frac{S_{n}}{T_{n}}=\frac{3n + 39}{n + 3}$，则使得$\frac{a_{n}}{b_{n}}$为整数的正整数$n$的值可以是（ ）
A. 2
B. 3
C. 4
D. 14

答案： ACD 由题意可得$\frac{S_{2n - 1}}{T_{2n - 1}}=\frac{\frac{(2n - 1)(a_{1}+a_{2n - 1})}{2}}{\frac{(2n - 1)(b_{1}+b_{2n - 1})}{2}}=\frac{(2n - 1)a_{n}}{(2n - 1)b_{n}}=\frac{a_{n}}{b_{n}}$，则$\frac{a_{n}}{b_{n}}=\frac{S_{2n - 1}}{T_{2n - 1}}=\frac{3(2n - 1)+39}{2n - 1+3}=\frac{3n + 18}{n + 1}=3+\frac{15}{n + 1}$.由$\frac{a_{n}}{b_{n}}$为整数，可知$n + 1$为$15$的正约数，则$n + 1$的可能取值有$3,5,15$，因此，正整数$n$的可能取值有$2,4,14$.

9. （2024·张家口检测）若数列$\{a_{n}\}$满足$a_{n}+a_{n + 1}=5n$，$a_{1}=1$，则$a_{2024}=$________.

答案： 5059
解析：
∵$a_{n}+a_{n + 1}=5n$，
∴当$n\geq2$时，$a_{n - 1}+a_{n}=5n - 5$，
∴$a_{n + 1}-a_{n - 1}=5$.又
∵$a_{1}=1$，$a_{1}+a_{2}=5$，
∴$a_{2}=4$.$\therefore a_{2024}$是首项为$4$，公差为$5$的等差数列的第$1012$项，$\therefore a_{2024}=4+(1012 - 1)\times5=5059$.

10. 若一个等差数列至少存在两项为质数，则称该数列为$K$数列. 已知等差数列$\{a_{n}\}$的公差为4，且$\{a_{n}\}$为$K$数列，写出满足题意的$a_{1}$的一个值：________.

答案： 7（答案不唯一）
解析：由$K$数列的定义可得，数列至少有两项为质数且质数满足差值为$4$的整数倍，如可取质数$7,11$作为其中两项，此时该数列取$a_{1}=7$即可.

11. 如果一个数列从第2项起，每一项与它的前一项的乘积都等于同一个不为零的常数，那么这个数列叫做等积数列，这个常数叫做等积数列的公积. 已知数列$\{a_{n}\}$是等积数列，且$a_{1}=2$，公积为 - 6，则$a_{3}=$________；数列$\{a_{n}\}$的前$n$项和$S_{n}=$________.

答案： $S_{n}=\begin{cases}-\frac{n}{2},n为偶数\\\frac{-n + 5}{2},n为奇数\end{cases}$
解析：由数列$\{a_{n}\}$是等积数列且$a_{1}=2$，公积为$-6$，可得$a_{2}=-3$，$a_{3}=2$，$a_{4}=-3$，$\cdots$，则前$n$项和$S_{n}=2+( - 3)+2+( - 3)+\cdots$.当$n$为偶数时，有$\frac{n}{2}$个$2$，$\frac{n}{2}$个$-3$，$\therefore S_{n}=\frac{2n-3n}{2}=-\frac{n}{2}$.当$n$为奇数时，有$\frac{n + 1}{2}$个$2$，$\frac{n - 1}{2}$个$-3$，$\therefore S_{n}=2\cdot\frac{n + 1}{2}-3\cdot\frac{n - 1}{2}=\frac{-n + 5}{2}$.$\therefore S_{n}=\begin{cases}-\frac{n}{2},n为偶数\\\frac{-n + 5}{2},n为奇数\end{cases}$.

12. 已知$a_{n}=9\times(-\frac{1}{2})^{n - 1}-5(n\in\mathbf{N}^{*})$，存在常数$A,B\in\mathbf{R}$，使得$A\leqslant a_{n}\leqslant B$，则$B - A$的最小值为________.

答案： $\frac{27}{2}$
解析：因为$a_{n}=9\times(-\frac{1}{2})^{n - 1}-5$，且$A\leq a_{n}\leq B$，所以$A\leq(a_{n})_{\min}$，$(a_{n})_{\max}\leq B$.因为$a_{2n - 1}=9\times(-\frac{1}{2})^{2n - 2}-5=9\times(\frac{1}{2})^{2n - 2}-5$，所以$a_{1}＞a_{3}＞\cdots＞a_{2n - 1}＞-5$，因为$a_{2n}=9\times(-\frac{1}{2})^{2n - 1}-5=-9\times(\frac{1}{2})^{2n - 1}-5$，所以$a_{2}＜a_{4}＜\cdots＜a_{2n}＜-5$. 又$a_{1}=4$，$a_{2}=-\frac{19}{2}$，故$-\frac{19}{2}\leq a_{n}\leq4$，所以$A\leq-\frac{19}{2}$，$B\geq4$，$-A\geq\frac{19}{2}$，所以$B - A\geq\frac{27}{2}$，所以$B - A$的最小值为$\frac{27}{2}$.