《2024年绿色通道45分钟课时作业与单元测评数学选择性必修第二册》

1.（2023·浙江温州期末）已知函数$f(x)$在$x = 2$的附近可导，且$\lim\limits_{x\rightarrow2}\frac{f(x)-2}{x - 2}=-2$，$f(2)=2$，则曲线$f(x)$在$(2,f(2))$处的切线方程为（ ）
A. $2x + y - 6 = 0$
B. $2x - y - 2 = 0$
C. $x + 2y - 6 = 0$
D. $x - 2y + 2 = 0$

答案： A $\because\lim\limits_{x \to 2}\frac{f(x)-2}{x - 2}=-2,f(2)=2,\therefore$曲线$f(x)$在$x = 2$处的切线斜率为$k=-2$. 又切线过点$(2,2),\therefore$代入直线的点斜式方程得$y - 2=-2(x - 2)$,即$2x + y-6 = 0$. 故选 A.

2. 已知公差不为0的等差数列$\{a_{n}\}$满足$a_{3}^{2}=a_{1}a_{4}$，$S_{n}$为数列$\{a_{n}\}$的前$n$项和，则$\frac{S_{7}-S_{5}}{S_{5}-S_{3}}$的值为（ ）
A. -2
B. -3
C. 2
D. 3

答案： B 设等差数列$\{a_{n}\}$的公差为$d(d\neq0)$. 由$a_{2}^{2}=a_{1}a_{4}$得$(a_{1}+2d)^{2}=a_{1}(a_{1}+3d)$,整理可得$a_{1}=-4d\neq0$,则$\frac{S_{7}-S_{5}}{S_{5}-S_{3}}=\frac{a_{6}+a_{7}}{a_{4}+a_{5}}=\frac{2a_{1}+11d}{2a_{1}+7d}=\frac{3d}{-d}=-3$. 故选 B.

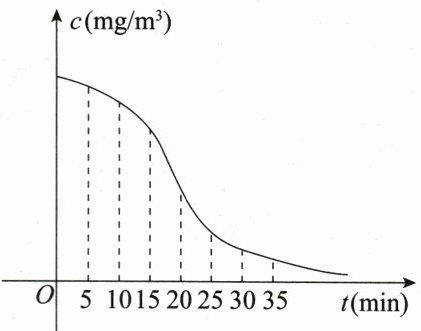
3. 降低室内微生物密度的有效方法是定时给室内注入新鲜空气，即开窗通风换气. 在某室内，空气中微生物密度$(c)$随开窗通风换气时间$(t)$的关系如图所示，则下列时间段内，空气中微生物密度变化的平均速度最快的是（ ）

A. $[5,10]$
B. $[5,15]$
C. $[5,20]$
D. $[5,35]$

答案：
C 如图,分别令$t = 5,t = 10,t = 15,t = 20,t = 35$所对应的点为$A,B,C,D,E$,由图可知$0＞k_{AB}＞k_{AC}＞k_{AE}＞k_{AD}$,所以$[5,20]$内空气中微生物密度变化的平均速度最快. 故选 C.

4. 已知数列$\{a_{n}\}$为正项等比数列，公比为$q$，又$b_{n}=\log_{2}a_{n}$，$n$为任意正整数，且数列$\{b_{n}\}$严格递减，则$q$的取值范围是（ ）
A. $(0,1)$
B. $(0,2)$
C. $(0,1)\cup(1,2)$
D. $(1,+\infty)$

答案： A 因为数列$\{b_{n}\}$严格递减,所以$b_{n + 1}＜b_{n}$,即$\log_{2}a_{n + 1}＜\log_{2}a_{n}$,即$\log_{2}\frac{a_{n + 1}}{a_{n}}＜0$,即$\log_{2}q＜0=\log_{2}1$,解得$0＜q＜1$,所以$q$的取值范围为$(0,1)$. 故选 A.

5. 已知函数$f(x)=x^{3}-4x$的定义域为$\mathbf{R}$，$g(x)=2\cos(x+\frac{\pi}{6})$的定义域为$(0,\pi)$，若曲线$g(x)$在$(x_{0},g(x_{0}))$处的切线斜率与曲线$f(x)$在$(1,f(1))$处的切线斜率相等，则$x_{0}=$（ ）
A. 0
B. $\frac{\pi}{6}$
C. $\frac{\pi}{2}$
D. $\frac{2\pi}{3}$

答案： D 因为$f(x)=x^{3}-4x$,所以$f^{\prime}(x)=3x^{2}-4$,其中$x\in\mathbf{R}$,又$g(x)=2\cos(x+\frac{\pi}{6})$,所以$g^{\prime}(x)=-2\sin(x+\frac{\pi}{6})$,其中$x\in(0,\pi)$,由题意可得$f^{\prime}(1)=g^{\prime}(x_{0})$,所以$-1=-2\sin(x_{0}+\frac{\pi}{6})$,且$x_{0}\in(0,\pi)$,所以$x_{0}+\frac{\pi}{6}=\frac{5\pi}{6}$,解得$x_{0}=\frac{2\pi}{3}$. 故选 D.

6. 曲线$f(x)=e^{-2x}+1$在点$(0,2)$处的切线与直线$y = 0$和$y = x$围成的三角形的面积为（ ）
A. $\frac{1}{3}$
B. $\frac{1}{2}$
C. $\frac{2}{3}$
D. 1

答案：
A 依题意得$f^{\prime}(x)=e^{-2x}\cdot(-2)=-2e^{-2x}$,则$f^{\prime}(0)=-2e^{-2\times0}=-2$. 曲线$y = e^{-2x}+1$在点$(0,2)$处的切线方程是$y - 2=-2x$,即$y=-2x + 2$. 在坐标系中作出直线$y=-2x + 2,y = 0$与$y = x$,直线$y=-2x + 2$与$y = x$的交点坐标是$(\frac{2}{3},\frac{2}{3})$,直线$y=-2x + 2$与$x$轴的交点坐标是$(1,0)$,结合图象可得,这三条直线所围成的三角形的面积等于$\frac{1}{2}\times1\times\frac{2}{3}=\frac{1}{3}$.\frac{2}{3}$\frac{2}{3}$0y−2x+2" page="31" src="https://thumb.zyjl.cn/pic23/656104/8a080b27cb4e48d7138182e6d086d50d.jpg?x-oss-process=image/crop,x_999,y_789,w_167,h_136/contrast,3">

7.（2023·浙江杭州第十四中学阶段考）若对于曲线$f(x)=-e^{x}-x$上任一点处的切线$l_{1}$，总存在曲线$g(x)=3ax + 2\cos x$上一点处的切线$l_{2}$，使得$l_{1}\perp l_{2}$，则实数$a$的取值范围是（ ）
A. $[-1,\frac{2}{3}]$
B. $[-\frac{2}{3},\frac{1}{3}]$
C. $(-\frac{1}{3},2)$
D. $[-\frac{1}{3},\frac{2}{3}]$

答案： D 由$f^{\prime}(x)=-e^{x}-1$,得曲线$f(x)$在$x = m$处的切线斜率为$f^{\prime}(m)=-e^{m}-1＜-1$. 由$g^{\prime}(x)=3a-2\sin x$,得曲线$g(x)$在$x = n$处的切线斜率为$g^{\prime}(n)=3a-2\sin n$,由题可得,$\forall m\in\mathbf{R}$,总存在$n\in\mathbf{R}$,使$g^{\prime}(n)=\frac{-1}{f^{\prime}(m)}$,即$3a-2\sin n=\frac{1}{e^{m}+1}\in(0,1)$,又$\sin n\in[-1,1]$,即$3a-2\sin n\in[3a - 2,3a + 2]$,故$(0,1)\subseteq[3a - 2,3a + 2]$,所以$\begin{cases}3a-2\leqslant0\\3a + 2\geqslant1\end{cases}$,解得$-\frac{1}{3}\leqslant a\leqslant\frac{2}{3}$,即$a\in[-\frac{1}{3},\frac{2}{3}]$.

8.（多选）数列$\{a_{n}\}$的各项均为正数，其前$n$项和为$S_{n}$，且满足$a_{n}\cdot S_{n}=9(n\in\mathbf{N}^{*})$，则下列四个结论中正确的是（ ）
A. $\{a_{n}\}$为等比数列
B. $\{a_{n}\}$为递减数列
C. $\{a_{n}\}$中存在大于3的项
D. $\{a_{n}\}$中存在小于$\frac{1}{2023}$的项

答案： BD 对于 A:假设数列$\{a_{n}\}$为等比数列,设其公比为$q$,$q＞0$,则$a_{2}^{2}=a_{1}a_{3}$,即$(\frac{9}{S_{2}})^{2}=\frac{81}{S_{1}S_{3}}$,所以$S_{2}^{2}=S_{1}S_{3}$,可得$a_{1}^{2}(1 + q)^{2}=a_{1}^{2}(1 + q+q^{2})$,解得$q = 0$,不合题意,故数列$\{a_{n}\}$不是等比数列,故 A 错误;
对于 B:当$n\geqslant2$时,$a_{n}=S_{n}-S_{n - 1}$. 因为$a_{n}\cdot S_{n}=9(n\in\mathbf{N}^{*})$,所以$S_{n}=\frac{9}{a_{n}}$,所以$a_{n}=\frac{9}{a_{n}}-\frac{9}{a_{n - 1}}=\frac{9(a_{n - 1}-a_{n})}{a_{n}a_{n - 1}}＞0$,可得$a_{n}＜a_{n - 1}$,所以数列$\{a_{n}\}$为递减数列,故 B 正确;
对于 C:由题意可知,$\forall n\in\mathbf{N}^{*},a_{n}＞0$,当$n = 1$时,$a_{1}^{2}=9$,可得$a_{1}=3$,由 B 知数列$\{a_{n}\}$为递减数列,故 C 错误;
对于 D:因为数列$\{a_{n}\}$的各项均为正数,其前$n$项和为$S_{n}$,所以随着$n$的增大,$S_{n}$递增. 而$a_{n}\cdot S_{n}=9(n\in\mathbf{N}^{*})$恒成立,所以$a_{n}=\frac{9}{S_{n}}$递减,且$a_{n}＞0$,所以$\{a_{n}\}$中必存在小于$\frac{1}{2023}$的项,故 D 正确. 故选 BD.

9.（2024·河南洛阳期末）已知$a$为实数，函数$f(x)=x^{3}+ax^{2}+(a - 3)x$的导函数为$f'(x)$，若$f'(x)$是偶函数，则$a =$_______.

答案： 0
解析 因为$f(x)=x^{3}+ax^{2}+(a - 3)x$,所以$f^{\prime}(x)=3x^{2}+2ax+a - 3$. 因为$f^{\prime}(x)$是偶函数,所以$f^{\prime}(-x)=f^{\prime}(x)$,即$3\times(-x)^{2}+2a\times(-x)+a - 3=3x^{2}+2ax+a - 3$,即$4ax = 0$,所以$a = 0$.

10. 已知数列$\{a_{n}\}$满足$a_{1}a_{2}a_{3}\cdots a_{n}=n^{2}(n\in\mathbf{N}^{*})$，则$a_{n}=$_______.

答案： $\begin{cases}1,n = 1\\\frac{n^{2}}{(n - 1)^{2}},n\geqslant2,n\in\mathbf{N}^{*}\end{cases}$
解析 因为$a_{1}a_{2}a_{3}\cdots a_{n}=n^{2}(n\in\mathbf{N}^{*})$,所以当$n = 1$时,$a_{1}=1$;
当$n\geqslant2$时,$a_{1}a_{2}a_{3}\cdots a_{n - 1}=(n - 1)^{2}$,两式相除得$a_{n}=\frac{n^{2}}{(n - 1)^{2}}(n\geqslant2,n\in\mathbf{N}^{*})$.
又当$n = 1$时,$a_{1}=1$不符合上式,
所以$a_{n}=\begin{cases}1,n = 1\\\frac{n^{2}}{(n - 1)^{2}},n\geqslant2,n\in\mathbf{N}^{*}\end{cases}$.

11. 若曲线$f(x)=(x + a)\sin x + 1$在$x = 0$处的切线方程是$2x - y + b = 0$，则$a + b =$_______.

答案： 3
解析 由已知得$f^{\prime}(x)=\sin x+(x + a)\cos x$,
则$f^{\prime}(0)=\sin 0+(0 + a)\cos 0=a$,
当$x = 0$时,$f(0)=(0 + a)\sin 0+1=1$,
又曲线$f(x)=(x + a)\sin x+1$在$x = 0$处的切线方程是$2x - y + b = 0$,
$\therefore a = 2,-1 + b = 0$,即$b = 1,\therefore a + b = 3$.

12. 我们利用“错位相减”的方法可求等比数列的前$n$项和，进而可利用该法求数列$\{(2n - 1)\cdot3^{n}\}$的前$n$项和$S_{n}$，其操作步骤如下：
由于$S_{n}=1\times3^{1}+3\times3^{2}+\cdots+(2n - 1)\cdot3^{n}$，
$3S_{n}=1\times3^{2}+3\times3^{3}+\cdots+(2n - 1)\cdot3^{n + 1}$，
从而$2S_{n}=-3-(2\times3^{2}+\cdots+2\times3^{n})+(2n - 1)\cdot3^{n + 1}$，
所以$S_{n}=(n - 1)\cdot3^{n + 1}+3$.
用以上方法和结论可求数列$\{n^{2}\cdot3^{n}\}$的前$n$项和$T_{n}$，则$2T_{n}+3=$_______.

答案： $(n^{2}-n + 1)\cdot3^{n + 1}$
解析 由题意,得$T_{n}=1^{2}\times3^{1}+2^{2}\times3^{2}+\cdots +n^{2}\cdot3^{n}$,
$3T_{n}=1^{2}\times3^{2}+2^{2}\times3^{3}+\cdots +n^{2}\cdot3^{n + 1}$,
两式相减得$2T_{n}=-3+(1^{2}-2^{2})\cdot3^{2}+(2^{2}-3^{2})\cdot3^{3}+\cdots+[(n - 1)^{2}-n^{2}]\cdot3^{n}+n^{2}\cdot3^{n + 1}$,
即$2T_{n}=-3-[3\cdot3^{2}+5\cdot3^{3}+\cdots+(2n - 1)\cdot3^{n}]+n^{2}\cdot3^{n + 1}$,
即$2T_{n}=-3-(S_{n}-3)+n^{2}\cdot3^{n + 1}$,
即$2T_{n}=-S_{n}+n^{2}\cdot3^{n + 1}=-[(n - 1)\cdot3^{n + 1}+3]+n^{2}\cdot3^{n + 1}=(n^{2}-n + 1)\cdot3^{n + 1}-3$,
所以$2T_{n}+3=(n^{2}-n + 1)\cdot3^{n + 1}$.