《2025年黄冈金牌之路练闯考七年级数学下册北师大版》

9.如图，AD所在的直线是△ABC的对称轴，若BD = 3，AD = 6，则图中阴影部分的面积为 （ ）

第9题图 第10题图
A.6
B.8
C.9
D.18

答案： C

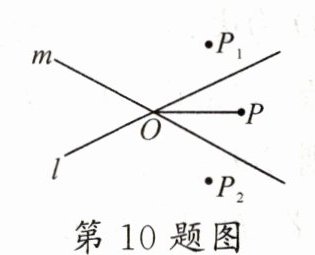
10.如图，直线l，m相交于点O，P为这两直线外的一点，且OP = 2.8.若点P关于直线l，m的对称点分别是点P1，P2，则P1，P2两点之间的距离可能是 （ ）

A.0
B.5
C.6
D.7

答案： B

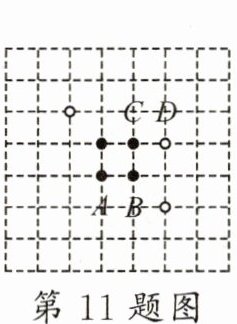
11.新情境 传统文化 （2024·甘肃）围棋起源于我国，古代称为“弈”.如图是两位同学的部分对弈图，轮到白方落子，观察棋盘，白方如果落子于点______的位置，则所得的对弈图是轴对称图形（填写A，B，C，D中的一处即可，A，B，C，D位于棋盘的格点上）.

第11题图 第12题图

答案： A或C

12.如图，△ADC和△EBC均与△ABC成轴对称，对称轴分别是直线AC，BC，若AD⊥BE，则∠ACB = ______.

答案： $135^{\circ}$

13.（16分）如图，△ABC和△ADE关于直线MN对称，BC和DE的交点F在直线MN上.
（1）若BC = 15，DF = 9，求EF的长；
（2）若∠ABC = 35°，∠AED = 65°，∠BAE = 16°，求∠CAN的度数；
（3）连接BD，CE，试判断BD与CE的位置关系，并说明理由.

答案： 解：
(1)因为$\triangle ABC$和$\triangle ADE$关于直线$MN$对称，所以$DE = BC = 15$，所以$EF=DE - DF=15 - 9 = 6$
(2)因为$\triangle ABC$和$\triangle ADE$关于直线$MN$对称，所以$\angle ACB=\angle AED = 65^{\circ}$，$\angle CAN=\angle EAN=\frac{1}{2}\angle CAE$，所以$\angle BAC=180^{\circ}-\angle ABC-\angle ACB=180^{\circ}-35^{\circ}-65^{\circ}=80^{\circ}$，所以$\angle CAE=\angle BAC-\angle BAE=80^{\circ}-16^{\circ}=64^{\circ}$，所以$\angle CAN=\frac{1}{2}\angle CAE=\frac{1}{2}\times64^{\circ}=32^{\circ}$
(3)$BD// CE$.理由如下：设$BD$交$MN$于点$G$，$CE$交$MN$于点$H$.因为$\triangle ABC$和$\triangle ADE$关于直线$MN$对称，所以$MN\perp BD$，$MN\perp CE$，所以$\angle AGD=\angle AHC = 90^{\circ}$，所以$BD// CE$

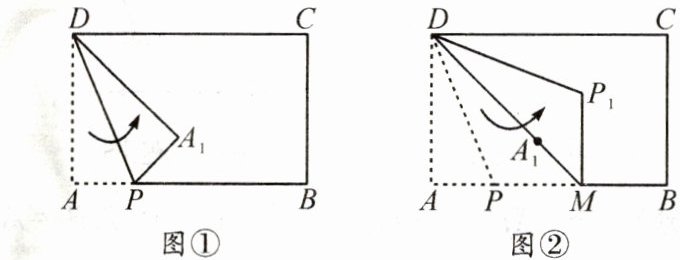
14.（20分）核心素养 几何直观 将一张长方形纸片ABCD按如下方式操作（P是AB上的一点）：
①如图①，将△PDA沿DP向内折叠，点A落在点A1处；
②如图②，延长DA1交边AB于点M，将△MDP沿DM向内继续折叠，点P落在点P1处.
若P1M⊥AB，求∠DP1M的度数.

图① 图②

答案： 解：因为将$\triangle MDP$沿$DM$向内继续折叠得到$\triangle MDP_1$，$P_1M\perp AB$，所以$\angle DMA=\angle DMP_1=\frac{1}{2}\angle P_1MA=\frac{1}{2}\times90^{\circ}=45^{\circ}$，$\angle PDM=\angle P_1DM$，所以$\angle ADM=90^{\circ}-\angle DMA = 45^{\circ}$.又因为将$\triangle PDA$沿$DP$向内折叠得到$\triangle PDA_1$，所以$\angle ADP=\angle PDM=\frac{1}{2}\angle ADM=22.5^{\circ}$，所以$\angle P_1DM=\angle PDM=22.5^{\circ}$，所以$\angle DP_1M=180^{\circ}-\angle P_1DM-\angle DMP_1=180^{\circ}-22.5^{\circ}-45^{\circ}=112.5^{\circ}$