《2025年黄冈金牌之路练闯考七年级数学下册北师大版》

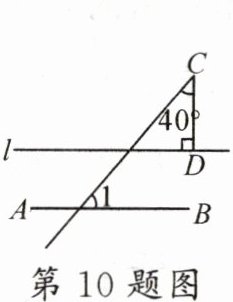
10.新考向 多模块综合 如图，已知l//AB，CD⊥l于点D，若∠C = 40°，则∠1的度数是（ ）

A.30°
B.40°
C.50°
D.60°

答案： C

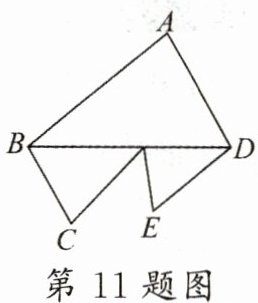
11.(葫芦岛中考)一个零件的形状如图所示，AB//DE，AD//BC，∠CBD = 60°，∠BDE = 40°，则∠A的度数是（ ）

A.70°
B.80°
C.90°
D.100°

答案： B

12.(抚顺中考)将两张三角形纸片如图摆放，量得∠1 + ∠2 + ∠3 + ∠4 = 220°，则∠5 = ______.

答案： 40°

13.将一副直角三角尺如图放置，已知∠E = 60°，∠C = 45°，EF//BC，则∠BGD = ______°.

答案： 105

14.(12分)如图，将一块直角三角尺DEF放置在锐角△ABC上，使得该三角尺的两条直角边DE，DF恰好分别经过△ABC的顶点B，C.若∠A = 40°，求∠ABD + ∠ACD的度数.

答案： 解:因为∠A=40°,所以∠ABC+∠ACB=180°−∠A=140°.又因为∠BDC=90°,所以∠DBC+∠DCB=90°,所以∠ABD+∠ACD=∠ABC+∠ACB−(∠DBC+∠DCB)=140°−90°=50°

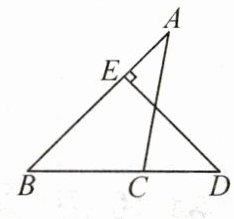
15.(10分)如图，D为△ABC的边BC延长线上的一点，DE⊥AB于点E，若∠A = 35°，∠D = 45°，求∠ACD的度数.

答案： 解:因为DE⊥AB,∠D=45°,所以∠B=90°一∠D=45°.又因为∠A=35°,所以∠ACB=180°−∠A−∠B=180°−35°−45°=100°,所以∠ACD=180°−∠ACB=180°−100°=80°

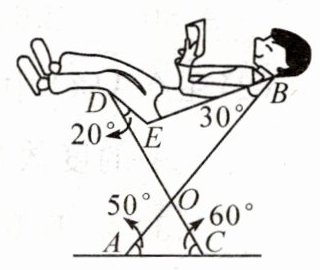
16.(16分)核心素养 模型观念 如图是某公司研发的一款可调躺椅的示意图(数据如图所示)，AB与CD的交点为O，∠OAC，∠OCA，∠OBE的度数保持不变，可通过调整∠ODE的大小来调整椅子的舒适程度.现为了舒适，需调整∠ODE的大小使得∠E = 110°，则应对∠ODE做出怎样的调整?

答案： 解:连接BD.因为∠OAC=50°,∠OCA=60°,所以∠A0C=180°−∠0AC−∠0CA=70°,所以∠BOD=∠AOC=70°.又因为当∠E=110°时,∠EBD+∠EDB=180°−∠E=70°,所以此时∠ODE=180°−∠BOD−∠OBE−∠EBD−∠EDB=180°−∠BOD−∠OBE−(∠EBD+∠EDB)=180°−70°−30°−70°=10°,所以应将∠ODE减小20°−10°=10°