《2025年少年班七年级数学下册浙教版浙江专版》

1. 如图，点G在CD上，已知∠BAG + ∠AGD = 180°，AE平分∠BAG，GF平分∠AGC. 请说明AE//GF.
解：因为∠BAG + ∠AGD = 180°（已知），
∠AGC + ∠AGD = 180°（邻补角的性质），
所以∠BAG = ∠AGC(______________).
因为AE平分∠BAG，
所以∠1 = $\frac{1}{2}$∠BAG(______________).
因为GF平分∠AGC，
所以∠2 = $\frac{1}{2}$________，
得∠1 = ∠2（等量代换），
所以________(______________).

答案： 同角的补角相等 角平分线的定义 ∠AGC AE//GF 内错角相等,两直线平行

2. [2024·浙江绍兴期末]如图，点E，F，G分别在直线CD，AB，AD上，EF交AD于点G，已知∠A = ∠D，∠CEF + ∠B = 180°.
(1)EF与BH平行吗？请说明理由.
(2)若∠DGE = 110°，求∠BHD的度数.

答案： 解
(1)EF//BH. 理由如下:
∵∠A=∠D,
∴AB//CD,
∴∠CEF+∠AFE=180°.
∵∠CEF+∠B=180°,
∴∠AFE=∠B,
∴EF//BH.
(2)
∵∠DGE=110°,
∴∠FGH=180°-∠DGE=70°.
由
(1)知EF//BH,
∴∠BHD=∠FGH=70°.

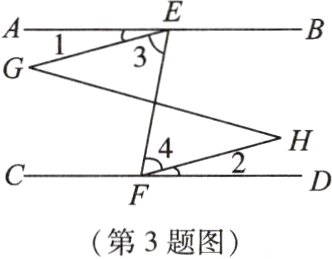
3. [2023·浙江台州期末]如图，已知直线EF分别交直线AB，CD于点E，F，∠1 = ∠2，∠BEF + ∠EFD = 180°，试说明∠G = ∠H.
解：∵∠BEF + ∠EFD = 180°（已知），
∴AB//CD(______________)，
∴∠AEF = ∠EFD(______________).
∵∠1 = ∠2（已知），
∴∠AEF - ∠1 = ∠EFD - ∠2，
即________ = ________.
∴________//________(____________)，
∴∠G = ∠H(____________).

答案： 同旁内角互补,两直线平行 两直线平行,内错角相等 ∠3 ∠4 GE FH 内错角相等,两直线平行 两直线平行,内错角相等

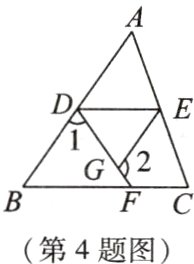
4. [2023·浙江宁波期末]如图，D，E，F三点分别在△ABC的AB，AC，BC边上，连接DE，DF，G是线段DF上的点，连接EG，已知∠1 + ∠2 = 180°.
(1)判断AB与EG的位置关系，并说明理由.
(2)若DE//BC，EG平分∠DEC，∠C = 70°，求∠B的度数.

答案： 解
(1)AB//EG. 理由如下:
∵∠1+∠2=180°,∠2+∠DGE=180°,
∴∠1=∠DGE,
∴AB//EG.
(2)
∵DE//BC,∠C=70°,
∴∠DEC=110°.
∵EG平分∠DEC,
∴∠DEG= $\frac{1}{2}$∠DEC=55°.
∵AB//EG,
∴∠ADE=∠DEG=55°.
∵DE//BC,
∴∠B=∠ADE=55°.