《2025年少年班七年级数学下册浙教版浙江专版》

1 [2024·浙江温州期中]计算$(x + 1)(x^{2}-2)$，所得结果的一次项系数是 （ ）
A. -2
B. -1
C. 1
D. 2

答案： A

2 [2023·浙江宁波期末]计算$(a - 1)(a^{2}+a + 1)$的结果是 （ ）
A. 1 - a^{3}
B. a^{3}-1
C. a^{3}-2a + 1
D. a^{3}+1

答案： B

3 [2023·浙江金华模拟]化简$(2x + 1)(x - 1)-(x^{2}+x - 2)$的结果是 （ ）
A. x^{2}-2x + 1
B. x^{2}-2x - 3
C. x^{2}+x - 3
D. x^{2}-3

答案： A

4 [2024·浙江温州期中]若关于x的多项式的乘积$(x^{2}+ax + 2)(x - 2)$化简后不含x^{2}项，则a的值是 （ ）
A. -2
B. 0
C. 0.5
D. 2

答案： D 解析：
∵$(x^{2}+ax + 2)(x - 2)=x^{3}-2x^{2}+ax^{2}-2ax + 2x - 4$，不含$x^{2}$项，
∴$-2x^{2}+ax^{2}=(-2 + a)x^{2}=0$，
∴$a = 2$. 故选D.

5 链接教材P89作业题第1题改编 计算：
(1)$(5x + 2y)(3x - 2y)$；
(2)$(2x - 3y)(3x + 2y - 1)$；
(3)$(3x^{2}+2x + 1)(2x^{2}+3x - 1)$.

答案： 解：
(1)原式$=15x^{2}-4xy - 4y^{2}$.
(2)原式$=6x^{2}+4xy - 2x - 9xy - 6y^{2}+3y=6x^{2}-5xy - 6y^{2}-2x + 3y$.
(3)原式$=6x^{4}+4x^{3}+2x^{2}+9x^{3}+6x^{2}+3x - 3x^{2}-2x - 1=6x^{4}+13x^{3}+5x^{2}+x - 1$.

6 先化简，再求值：
(1)$(x - 2y)(x + 3y)+(2x - y)(x - 4y)$，其中x = -1，y = 2.
(2)$(x - 2y)(x + 2y - 1)+4y^{2}$，其中x = $\frac{1}{2}$，y = -1.

答案： 解：
(1)$(x - 2y)(x + 3y)+(2x - y)(x - 4y)$
$=x^{2}+3xy - 2xy - 6y^{2}+(2x^{2}-8xy - xy + 4y^{2})$
$=x^{2}+3xy - 2xy - 6y^{2}+2x^{2}-8xy - xy + 4y^{2}$
$=3x^{2}-8xy - 2y^{2}$.
当$x = - 1$，$y = 2$时，
原式$=3\times(-1)^{2}-8\times(-1)\times2-2\times2^{2}=3 + 16 - 8=11$.
(2)$(x - 2y)(x + 2y - 1)+4y^{2}$
$=(x - 2y)(x + 2y)-(x - 2y)+4y^{2}$
$=x^{2}-4y^{2}-x + 2y + 4y^{2}$
$=x^{2}-x + 2y$.
当$x=\frac{1}{2}$，$y = - 1$时，原式$=\frac{1}{4}-\frac{1}{2}-2=-2\frac{1}{4}$.

7 [2023·浙江杭州西湖模拟]解方程：x^{2}-(x + 3)·(x - 1)=4x - 1.

答案： 解：$x^{2}-(x + 3)(x - 1)=4x - 1$.
$x^{2}-(x^{2}+2x - 3)=4x - 1$.
$-2x + 3=4x - 1$.
$-6x=-4$.
$x=\frac{2}{3}$.

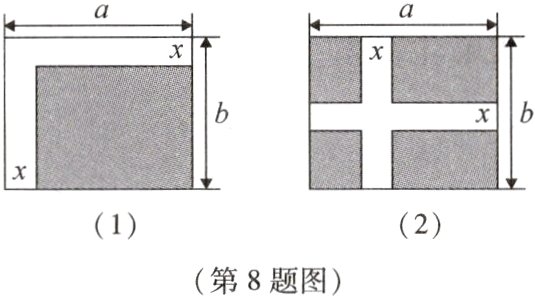
8 [2024·浙江杭州月考]通过计算，比较图(1)、图(2)中阴影部分的面积，可以验证的算式是 （ ）

A. a(b - x)=ab - ax
B. (a - x)(b - x)=ab - ax - bx + x^{2}
C. (a - x)(b - x)=ab - ax - bx
D. b(a - x)=ab - bx

答案： B 解析：题图
(1)中，阴影部分的面积为$(a - x)(b - x)$. 题图
(2)中，阴影部分的面积为$ab - ax - bx + x^{2}$，所以$(a - x)\cdot(b - x)=ab - ax - bx + x^{2}$. 故选B.