《2025年少年班七年级数学下册浙教版浙江专版》

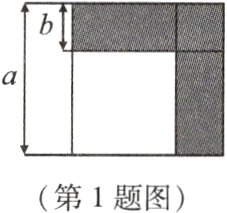
1. 我们已经接触了很多代数恒等式，知道可以用一些硬纸片拼成的图形面积来解释一些代数恒等式. 通过图中阴影部分面积的计算，验证了一个恒等式，此等式是（ ）

A. $a^{2}-b^{2}=(a + b)(a - b)$
B. $(a - b)^{2}=a^{2}-2ab + b^{2}$
C. $(a + b)^{2}=a^{2}+2ab + b^{2}$
D. $(a - b)(a + 2b)=a^{2}+ab - b^{2}$

答案： B 解析 由题图得$S_{空白正方形}=(a - b)^{2}=a^{2}-2b(a - b)-b^{2}=a^{2}-2ab + b^{2}$,$\therefore(a - b)^{2}=a^{2}-2ab + b^{2}$. 故选 B.

2. 如图(1)，把一个长为2m，宽为2n的长方形沿虚线用剪刀均分成四个小长方形，然后拼成一个正方形，如图(2).
(1)请用两种不同的方法求图(2)中阴影部分的面积(直接用含m，n的代数式表示).

方法1：__________________________；
方法2：__________________________.
(2)根据(1)中的结论，请你写出下列三个代数式$(m + n)^{2}$，$(m - n)^{2}$，$mn$间的等量关系：__________________________.
(3)根据(2)中的等量关系，解决下列问题：已知实数x，y满足$xy = 5$，$x = y + 4$，请求出$(x + y)^{2}$的值.

答案： 解
(1)$(m - n)^{2}$ $(m + n)^{2}-4mn$.
(2)$(m + n)^{2}=(m - n)^{2}+4mn$.
(3)$\because x = y + 4$,$\therefore x - y = 4$.
$\because xy = 5$,
$\therefore(x + y)^{2}=(x - y)^{2}+4xy = 4^{2}+4×5 = 36$.

3. [2023·浙江台州期中]计算$(x - 1)^{2}$的结果是（ ）
A. $x^{2}+1$
B. $x^{2}-1$
C. $x^{2}-2x + 1$
D. $x^{2}+2x + 1$

答案： C

4. 链教材P93课内练习第1题改编 运用完全平方公式计算：
(1)$(3a + b)^{2}$；
(2)$(-x - y)^{2}$；
(3)$(-2x + 3y)^{2}$；
(4)$(a + b - 1)^{2}$.

答案： 解
(1)原式$=9a^{2}+6ab + b^{2}$.
(2)原式$=x^{2}+2xy + y^{2}$.
(3)原式$=4x^{2}-12xy + 9y^{2}$.
(4)原式$=[(a + b)-1]^{2}=(a + b)^{2}-2(a + b)+1=a^{2}+2ab + b^{2}-2a - 2b + 1$.

5. 有一块正方形木板，它的边长是$(2m + 5)cm$，现在从四个角上分别锯去一个边长是$(m - 2)cm$的小正方形，请你求出剩余木板的面积.

答案： 解 $(2m + 5)^{2}-4(m - 2)^{2}$
$=4m^{2}+20m + 25-4(m^{2}-4m + 4)$
$=4m^{2}+20m + 25-4m^{2}+16m - 16$
$=36m + 9(cm^{2})$.
所以剩余木板的面积为$(36m + 9)cm^{2}$.