8 下列图形,由∠1 = ∠2能得到AB//CD的是( )




答案:
A 解析:A.
∵∠1 = ∠2,
∴AB//CD,此选项符合题意; B. 由∠1 = ∠2,不能得到AB//CD,此选项不符合题意;C. 由∠1 = ∠2能得到AD//BC,此选项不符合题意; D. 如答图,
∵∠2与∠3不一定相等,∠1 = ∠2,
∴∠1与∠3不一定相等,
∴不能得到AB//CD,此选项不符合题意. 故选A.

A 解析:A.
∵∠1 = ∠2,
∴AB//CD,此选项符合题意; B. 由∠1 = ∠2,不能得到AB//CD,此选项不符合题意;C. 由∠1 = ∠2能得到AD//BC,此选项不符合题意; D. 如答图,
∵∠2与∠3不一定相等,∠1 = ∠2,
∴∠1与∠3不一定相等,
∴不能得到AB//CD,此选项不符合题意. 故选A.

9 [2024·浙江嘉兴期末]将一副三角板如图放置,边EF与边BC在同一条直线上,∠ACB = ∠DFE = 90°,∠ABC = 60°,∠E = 45°. 三角板DEF保持不动,将三角板ABC绕点B顺时针旋转α(0°<α<180°). 当α = ______°时,AB//DE.


答案:
15 解析:如答图. 当∠ABF = ∠E = 45°时,AB//DE,则∠FBC = ∠ABC - ∠ABF = 60° - 45° = 15°,
∴三角板ABC绕点B顺时针旋转15°,即α = 15°.

15 解析:如答图. 当∠ABF = ∠E = 45°时,AB//DE,则∠FBC = ∠ABC - ∠ABF = 60° - 45° = 15°,
∴三角板ABC绕点B顺时针旋转15°,即α = 15°.

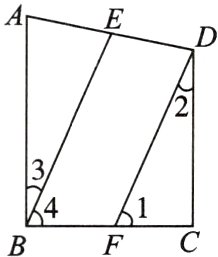
10 如图,AB⊥BC,∠1 + ∠2 = 90°,∠2 = ∠3. BE与DF平行吗?为什么?
解:BE//DF,理由如下:
∵ AB⊥BC,(已知)
∴ ∠ABC = 90°,即∠3 + ∠4 = 90°. (垂直的定义)
又∵ ∠1 + ∠2 = 90°,且∠2 = ∠3,(已知)
∴ ∠1 + ______ = 90°. (等量代换)
∴ ∠1 = ______. (__________)
∴ BE//DF. (__________)
解:BE//DF,理由如下:
∵ AB⊥BC,(已知)
∴ ∠ABC = 90°,即∠3 + ∠4 = 90°. (垂直的定义)
又∵ ∠1 + ∠2 = 90°,且∠2 = ∠3,(已知)
∴ ∠1 + ______ = 90°. (等量代换)
∴ ∠1 = ______. (__________)
∴ BE//DF. (__________)

答案:
∠3 ∠4 同角的余角相等 同位角相等,两直线平行
11 [2024·浙江宁波阶段练习]如图,点A,D,B在同一条直线上,∠ADE = ∠ABC,且DG,BF分别是∠ADE和∠ABC的平分线,DG与BF平行吗? 请说明理由.


答案:
解:DG与BF平行. 理由如下:
∵DG,BF分别是∠ADE和∠ABC的平分线,
∴∠ADG = $\frac{1}{2}$∠ADE,∠DBF = $\frac{1}{2}$∠ABC.
∵∠ADE = ∠ABC,
∴∠ADG = ∠DBF,
∴DG//BF(同位角相等,两直线平行).
∵DG,BF分别是∠ADE和∠ABC的平分线,
∴∠ADG = $\frac{1}{2}$∠ADE,∠DBF = $\frac{1}{2}$∠ABC.
∵∠ADE = ∠ABC,
∴∠ADG = ∠DBF,
∴DG//BF(同位角相等,两直线平行).
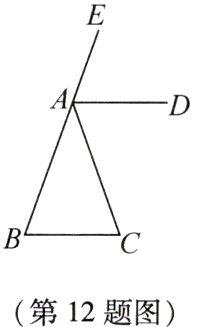
12 (核心素养·几何直观、推理能力)如图,已知∠ABC = 70°,∠BAC = 40°,AD平分∠CAE.
(1)求证:AD//BC.
(2)若射线AD绕点A以每秒1°的速度顺时针方向旋转得到AM,同时,射线CA绕点C以每秒2°的速度顺时针方向旋转得到CN,AM和CN交于点P,设旋转时间为t秒.
①当0<t<55时,请写出∠APC与∠BAP之间的数量关系,并说明理由.
②当0<t<70时,若$\frac{1}{5}$∠APC + ∠BCP = 180°,请直接写出t的值.

(1)求证:AD//BC.
(2)若射线AD绕点A以每秒1°的速度顺时针方向旋转得到AM,同时,射线CA绕点C以每秒2°的速度顺时针方向旋转得到CN,AM和CN交于点P,设旋转时间为t秒.
①当0<t<55时,请写出∠APC与∠BAP之间的数量关系,并说明理由.
②当0<t<70时,若$\frac{1}{5}$∠APC + ∠BCP = 180°,请直接写出t的值.


答案:
(1)证明:
∵∠BAC = 40°,
∴∠CAE = 180° - ∠BAC = 140°.
∵AD平分∠CAE,
∴∠DAE = $\frac{1}{2}$∠CAE = 70°.
∵∠ABC = 70°,
∴∠ABC = ∠DAE,
∴AD//BC.
(2)解:①
∵∠DAE = ∠DAC = 70°,射线AD绕点A以每秒1°的速度顺时针方向旋转得到AM,
∴∠CAM = 70° - t°.
∵∠BAC = 40°,
∴∠BAP = ∠BAC + ∠CAM = 40° + (70° - t°) = 110° - t°.
∵射线CA绕点C以每秒2°的速度顺时针方向旋转得到CN,
∴∠ACP = 2t°.
∴∠APC = 180° - ∠CAM - ∠ACP = 180° - (70° - t°) - 2t° = 110° - t°,
∴∠APC = ∠BAP.
②t的值为60或$\frac{440}{9}$. 求解过程如下:
当0 < t < 55时,如答图
(1).
由①,得∠APC = 110° - t°,∠ACP = 2t°,
∴∠BCP = 70° + 2t°.
∵$\frac{1}{5}$∠APC + ∠BCP = 180°,
∴$\frac{1}{5}$(110° - t°) + 70° + 2t° = 180°,
解得t = $\frac{440}{9}$.

当55 ≤ t < 70时,如答图
(2).
∵∠ACP = 2t°,∠ACB = 70°,
∴∠BCP = 360° - ∠ACB - ∠ACP = 360° - 70° - 2t° = 290° - 2t°.
∵∠APC = 110° - t°,$\frac{1}{5}$∠APC + ∠BCP = 180°,
∴$\frac{1}{5}$(110° - t°) + (290° - 2t°) = 180°,
解得t = 60.

综上可知,t的值为60或$\frac{440}{9}$.
(1)证明:
∵∠BAC = 40°,
∴∠CAE = 180° - ∠BAC = 140°.
∵AD平分∠CAE,
∴∠DAE = $\frac{1}{2}$∠CAE = 70°.
∵∠ABC = 70°,
∴∠ABC = ∠DAE,
∴AD//BC.
(2)解:①
∵∠DAE = ∠DAC = 70°,射线AD绕点A以每秒1°的速度顺时针方向旋转得到AM,
∴∠CAM = 70° - t°.
∵∠BAC = 40°,
∴∠BAP = ∠BAC + ∠CAM = 40° + (70° - t°) = 110° - t°.
∵射线CA绕点C以每秒2°的速度顺时针方向旋转得到CN,
∴∠ACP = 2t°.
∴∠APC = 180° - ∠CAM - ∠ACP = 180° - (70° - t°) - 2t° = 110° - t°,
∴∠APC = ∠BAP.
②t的值为60或$\frac{440}{9}$. 求解过程如下:
当0 < t < 55时,如答图
(1).
由①,得∠APC = 110° - t°,∠ACP = 2t°,
∴∠BCP = 70° + 2t°.
∵$\frac{1}{5}$∠APC + ∠BCP = 180°,
∴$\frac{1}{5}$(110° - t°) + 70° + 2t° = 180°,
解得t = $\frac{440}{9}$.

当55 ≤ t < 70时,如答图
(2).
∵∠ACP = 2t°,∠ACB = 70°,
∴∠BCP = 360° - ∠ACB - ∠ACP = 360° - 70° - 2t° = 290° - 2t°.
∵∠APC = 110° - t°,$\frac{1}{5}$∠APC + ∠BCP = 180°,
∴$\frac{1}{5}$(110° - t°) + (290° - 2t°) = 180°,
解得t = 60.

综上可知,t的值为60或$\frac{440}{9}$.
查看更多完整答案,请扫码查看


