《2025年步步高大二轮专题复习高中数学》

跟踪演练1　(2024·毕节模拟)在无穷数列$\{ a_{n}\}$中，若对任意的$n\in \mathbf{N}^{*}$，都存在$m\in \mathbf{N}^{*}$，使得$a_{n}+a_{n + 2m}=2a_{n + m}$，则称$\{ a_{n}\}$为$m$阶等差数列.在正项无穷数列$\{ b_{n}\}$中，若对任意的$n\in \mathbf{N}^{*}$，都存在$m\in \mathbf{N}^{*}$，使得$b_{n}b_{n + 2m}=b_{n + m}^{2}$，则称$\{ b_{n}\}$为$m$阶等比数列.
(1)若数列$\{ b_{n}\}$为1阶等比数列，$b_{1}+b_{2}+b_{3}=\frac{7}{2}$，$b_{3}+b_{4}+b_{5}=\frac{7}{8}$，求$\{ b_{n}\}$的通项公式及前$n$项和；
(2)若数列$\{ \ln c_{n}\}$为$m$阶等差数列，求证：$\{ c_{n}\}$为$m$阶等比数列；
(3)若数列$\{ \ln c_{n}\}$既是$m$阶等差数列，又是$m + 1$阶等差数列，证明：$\{ c_{n}\}$是等比数列.

答案：

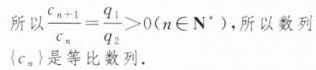
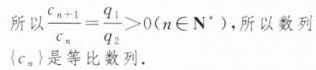
例2　(2024·泉州模拟)将足够多的一批规格相同、质地均匀的长方体薄铁块叠放于水平桌面上，每个铁块总比其下层铁块向外伸出一定的长度，如图，那么最上层的铁块最多可向桌沿外伸出多远而不掉下呢？这就是著名的“里拉斜塔”问题.将铁块从上往下依次标记为第1块、第2块、第3块、…、第$n$块，将前$i(i = 1,2,3,\cdots,n)$块铁块视为整体，若这部分的重心在第$(i + 1)$块的上方，且全部铁块整体的重心在桌面的上方，整批铁块就保持不倒.设这批铁块的长度均为1，若记第$n$块比第$(n + 1)$块向桌沿外多伸出的部分的最大长度为$a_{n}$，则根据力学原理，可得$a_{2}=\frac{1}{4}$，且$\{ \frac{1}{a_{n}}\}$为等差数列.

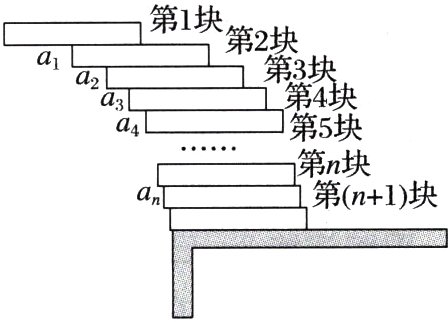
(1)求$\{ a_{n}\}$的通项公式；
(2)记数列$\{ a_{n}\}$的前$n$项和为$S_{n}$，
①比较$S_{n}$与$\frac{1}{2}\ln(n + 1)$的大小；
②对于无穷数列$\{ x_{n}\}$，如果存在常数$A$，对任意的正数$\varepsilon$，总存在正整数$N_{0}$，使得$\forall n ＞ N_{0}$，$\vert x_{n}-A\vert ＜ \varepsilon$，则称数列$\{ x_{n}\}$收敛于$A$，也称数列$\{ x_{n}\}$的极限为$A$，记为$\lim\limits_{n\rightarrow\infty}x_{n}=A$；反之，则称$\{ x_{n}\}$不收敛.请根据数列收敛的定义判断$\{ S_{n}\}$是否收敛？并据此回答“里拉斜塔”问题.

答案： 例2　解：
(1)依题意，第1块铁块比第2块铁块向桌沿外伸出部分的最大长度为第1块铁块自身长度的一半，则$a_1=1/2，$由${1/a_n}$为等差数列，得其首项为$1/a_1=2，$
公差$d=1/a_2-1/a_1=4 - 2=2，$
因此$1/a_n=1/a_1+(n - 1)d=2+2(n - 1)=2n，$
即$a_n=1/2n，$
所以${a_n}$的通项公式是$a_n=1/2n。$
(2)①由
(1)知，$S_n=1/2+1/4+1/6+⋯+1/2n=1/2(1+1/2+1/3+⋯+1/n)，$
令函数f(x)=ln⁡(1 + x)-x，x＞0，
求导得f'(x)=1/(1 + x)-1＜0，即函数f(x)在(0，+∞)上单调递减，
则f(x)＜f
(0)=0，即ln⁡(1 + x)＜x，
取x=1/n，
于是1/n＞ln⁡(1+1/n)=ln⁡(n + 1)-ln⁡n，
则1+1/2+1/3+⋯+1/n＞ln⁡2-ln⁡1+ln⁡3-ln⁡2+ln⁡4-ln⁡3+⋯+ln⁡(n + 1)-ln⁡n=ln⁡(n + 1)，
所以$S_n＞1/2ln⁡(n + 1)。$$②{S_n}$不收敛。
给定正数A，对∀ε＞0，
令|1/2ln⁡(n + 1)-A|＜ε，
则A - ε＜1/2ln⁡(n + 1)＜A + ε，
解得e^(2(A - ε))-1＜n＜e^(2(A + ε))-1，
取N_0=[e^(2(A + ε))-1]([x]表示不超过x的最大整数)，
显然当n＞$N_0$时，不等式|1/2ln⁡(n + 1)-A|＜ε不成立，
即有1/2ln⁡(n + 1)＞A + ε，
因此数列{1/2ln⁡(n + 1)}不收敛，
则由①可知，当$n＞N_0$时，$S_n - A＞1/2ln⁡(n + 1)-A＞ε，$
因此当$n＞N_0$时，$|S_n - A|＜ε$不成立，所以${S_n}$不收敛。${S_n}$的意义是n块叠放的铁块最上层的最多可向桌沿外伸出的长度，因为${S_n}$不收敛于任意正数A，
所以只要铁块足够多，最上层的铁块最多可向桌沿外伸出的长度可以大于任意正数。