2025年步步高大二轮专题复习高中数学
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年步步高大二轮专题复习高中数学 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第37页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
跟踪演练2 (多选)(2024·通化模拟)奔驰定理的几何表示因酷似奔驰的标志得来,是平面向量中一个非常优美的结论,它与三角形四心(重心、内心、外心、垂心)有着神秘的关联.具体内容是:已知M是△ABC内一点,△BMC,△AMC,△AMB的面积分别为$S_{A}$,$S_{B}$,$S_{C}$,则$S_{A}\cdot\overrightarrow{MA}+S_{B}\cdot\overrightarrow{MB}+S_{C}\cdot\overrightarrow{MC}=\boldsymbol{0}$.以下命题正确的有 ( )
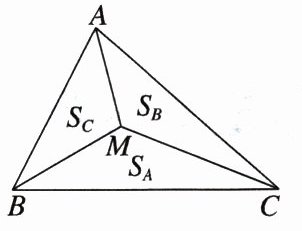
A.若$S_{A}:S_{B}:S_{C}=1:1:1$,则M为△ABC的重心
B.若M为△ABC的内心,则$BC\cdot\overrightarrow{MA}+AC\cdot\overrightarrow{MB}+AB\cdot\overrightarrow{MC}=\boldsymbol{0}$
C.若∠BAC = 45°,∠ABC = 60°,M为△ABC的外心,则$S_{A}:S_{B}:S_{C}=2:\sqrt{3}:1$
D.若M为△ABC的垂心,$3\overrightarrow{MA}+4\overrightarrow{MB}+5\overrightarrow{MC}=\boldsymbol{0}$,则$\cos\angle AMB=\frac{\sqrt{6}}{6}$

A.若$S_{A}:S_{B}:S_{C}=1:1:1$,则M为△ABC的重心
B.若M为△ABC的内心,则$BC\cdot\overrightarrow{MA}+AC\cdot\overrightarrow{MB}+AB\cdot\overrightarrow{MC}=\boldsymbol{0}$
C.若∠BAC = 45°,∠ABC = 60°,M为△ABC的外心,则$S_{A}:S_{B}:S_{C}=2:\sqrt{3}:1$
D.若M为△ABC的垂心,$3\overrightarrow{MA}+4\overrightarrow{MB}+5\overrightarrow{MC}=\boldsymbol{0}$,则$\cos\angle AMB=\frac{\sqrt{6}}{6}$
答案:
跟踪演练2 ABC
1.(2024·安庆模拟)设O点在△ABC内部,且有$3\overrightarrow{OA}+2\overrightarrow{OB}+\overrightarrow{OC}=\boldsymbol{0}$,则△AOC的面积与△AOB的面积的比值为 ( )
A.2 B.$\sqrt{3}$ C.$\sqrt{2}$ D.3
A.2 B.$\sqrt{3}$ C.$\sqrt{2}$ D.3
答案:
思维提升 拓展练习
1. A
1. A
2.设I为△ABC的内心,且$2\overrightarrow{IA}+3\overrightarrow{IB}+\sqrt{7}\overrightarrow{IC}=\boldsymbol{0}$,则角C为 ( )
A.$\frac{\pi}{6}$ B.$\frac{\pi}{3}$ C.$\frac{2\pi}{3}$ D.$\frac{3\pi}{4}$
A.$\frac{\pi}{6}$ B.$\frac{\pi}{3}$ C.$\frac{2\pi}{3}$ D.$\frac{3\pi}{4}$
答案:
2. B
3.已知△ABC的重心为G,AB = 6,AC = 8,BC = $2\sqrt{13}$,则△BGC的面积为 ( )
A.$12\sqrt{3}$ B.$8\sqrt{3}$ C.$4\sqrt{3}$ D.4
A.$12\sqrt{3}$ B.$8\sqrt{3}$ C.$4\sqrt{3}$ D.4
答案:
3. C
4.在△ABC中,AB = 2,AC = 3,BC = 4,O为△ABC的内心,若$\overrightarrow{AO}=\lambda\overrightarrow{AB}+\mu\overrightarrow{BC}$,则3λ + 6μ的值为 ( )
A.1 B.2 C.3 D.7
A.1 B.2 C.3 D.7
答案:
4. C
5.已知点A,B,C,P在同一平面内,$\overrightarrow{PQ}=\frac{1}{3}\overrightarrow{PA}$,$\overrightarrow{QR}=\frac{1}{3}\overrightarrow{QB}$,$\overrightarrow{RP}=\frac{1}{3}\overrightarrow{RC}$,则$S_{\triangle ABC}:S_{\triangle PBC}$等于 ( )
A.$\frac{19}{6}$ B.$\frac{3}{2}$ C.$\frac{5}{3}$ D.$\frac{19}{4}$
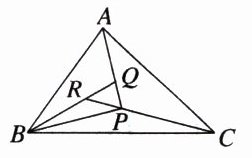
A.$\frac{19}{6}$ B.$\frac{3}{2}$ C.$\frac{5}{3}$ D.$\frac{19}{4}$

答案:
5. D
6.奔驰定理:已知点O是△ABC内的一点,若△BOC,△AOC,△AOB的面积分别记为$S_{1}$,$S_{2}$,$S_{3}$,则$S_{1}\cdot\overrightarrow{OA}+S_{2}\cdot\overrightarrow{OB}+S_{3}\cdot\overrightarrow{OC}=\boldsymbol{0}$. “奔驰定理”是平面向量中一个非常优美的结论,因为这个定理对应的图形与“奔驰”轿车的标志很相似,故形象地称其为“奔驰定理”.如图,已知O是△ABC的垂心,且$\overrightarrow{OA}+2\overrightarrow{OB}+3\overrightarrow{OC}=\boldsymbol{0}$,则cos C = ( )

A.$\frac{3\sqrt{10}}{10}$ B.$\frac{\sqrt{10}}{10}$ C.$\frac{2\sqrt{5}}{5}$ D.$\frac{\sqrt{5}}{5}$

A.$\frac{3\sqrt{10}}{10}$ B.$\frac{\sqrt{10}}{10}$ C.$\frac{2\sqrt{5}}{5}$ D.$\frac{\sqrt{5}}{5}$
答案:
6. B [延长$CO$交$AB$于点$P$,
$\because O$是$\triangle ABC$的垂心,$\therefore OP\perp AB$。
$\therefore S_{1}:S_{2} = (\frac{1}{2}\cdot OC\cdot BP):(\frac{1}{2}\cdot OC\cdot AP)$
$= BP:AP = (OP\tan\angle POB):(OP\tan\angle POA)$
$= \tan\angle COB:\tan\angle COA$
$= \tan(\pi - A):\tan(\pi - B)$
$= \tan A:\tan B$。
同理可得$S_{2}:S_{3} = \tan B:\tan C$,
$\therefore S_{1}:S_{2}:S_{3} = \tan A:\tan B:\tan C$。
又$S_{1}\cdot\overrightarrow{OA} + S_{2}\cdot\overrightarrow{OB} + S_{3}\cdot\overrightarrow{OC} = 0$,
$\therefore \tan A\cdot\overrightarrow{OA} + \tan B\cdot\overrightarrow{OB} + \tan C\cdot\overrightarrow{OC} = 0$。
又$\overrightarrow{OA} + 2\overrightarrow{OB} + 3\overrightarrow{OC} = 0$,
$\therefore \tan A:\tan B:\tan C = 1:2:3$。
不妨设$\tan A = k$,$\tan B = 2k$,$\tan C = 3k$,其中$k \neq 0$。
$\because \tan A = -\tan(B + C) = -\frac{\tan B + \tan C}{1 - \tan B\tan C}$,
$\therefore k = -\frac{2k + 3k}{1 - 2k\cdot 3k}$,解得$k = \pm 1$。
当$k = -1$时,
此时$\tan A < 0$,$\tan B < 0$,$\tan C < 0$,
则$A$,$B$,$C$都是钝角,不符合题意,舍去。
故$k = 1$,则$\tan C = 3 > 0$,
故$C$为锐角,
$\therefore \begin{cases} \frac{\sin C}{\cos C} = 3, \\ \sin^{2}C + \cos^{2}C = 1, \end{cases}$
解得$\cos C = \frac{\sqrt{10}}{10}$。

]
6. B [延长$CO$交$AB$于点$P$,
$\because O$是$\triangle ABC$的垂心,$\therefore OP\perp AB$。
$\therefore S_{1}:S_{2} = (\frac{1}{2}\cdot OC\cdot BP):(\frac{1}{2}\cdot OC\cdot AP)$
$= BP:AP = (OP\tan\angle POB):(OP\tan\angle POA)$
$= \tan\angle COB:\tan\angle COA$
$= \tan(\pi - A):\tan(\pi - B)$
$= \tan A:\tan B$。
同理可得$S_{2}:S_{3} = \tan B:\tan C$,
$\therefore S_{1}:S_{2}:S_{3} = \tan A:\tan B:\tan C$。
又$S_{1}\cdot\overrightarrow{OA} + S_{2}\cdot\overrightarrow{OB} + S_{3}\cdot\overrightarrow{OC} = 0$,
$\therefore \tan A\cdot\overrightarrow{OA} + \tan B\cdot\overrightarrow{OB} + \tan C\cdot\overrightarrow{OC} = 0$。
又$\overrightarrow{OA} + 2\overrightarrow{OB} + 3\overrightarrow{OC} = 0$,
$\therefore \tan A:\tan B:\tan C = 1:2:3$。
不妨设$\tan A = k$,$\tan B = 2k$,$\tan C = 3k$,其中$k \neq 0$。
$\because \tan A = -\tan(B + C) = -\frac{\tan B + \tan C}{1 - \tan B\tan C}$,
$\therefore k = -\frac{2k + 3k}{1 - 2k\cdot 3k}$,解得$k = \pm 1$。
当$k = -1$时,
此时$\tan A < 0$,$\tan B < 0$,$\tan C < 0$,
则$A$,$B$,$C$都是钝角,不符合题意,舍去。
故$k = 1$,则$\tan C = 3 > 0$,
故$C$为锐角,
$\therefore \begin{cases} \frac{\sin C}{\cos C} = 3, \\ \sin^{2}C + \cos^{2}C = 1, \end{cases}$
解得$\cos C = \frac{\sqrt{10}}{10}$。

]
7.(多选)(2024·保定模拟)“奔驰定理”是平面向量中一个非常优美的结论,因为这个定理对应的图形与“奔驰”轿车的标志很相似,所以形象地称其为“奔驰定理”.奔驰定理:已知O是△ABC内一点,△BOC,△AOC,△AOB的面积分别为$S_{A}$,$S_{B}$,$S_{C}$,则$S_{A}\cdot\overrightarrow{OA}+S_{B}\cdot\overrightarrow{OB}+S_{C}\cdot\overrightarrow{OC}=\boldsymbol{0}$.设O是△ABC内一点,△ABC的三个内角分别为A,B,C,△BOC,△AOC,△AOB的面积分别为$S_{A}$,$S_{B}$,$S_{C}$,若$3\overrightarrow{OA}+4\overrightarrow{OB}+5\overrightarrow{OC}=\boldsymbol{0}$,则以下命题正确的有 ( )

A.$S_{A}:S_{B}:S_{C}=3:4:5$
B.O有可能是△ABC的重心
C.若O为△ABC的外心,则$\sin A:\sin B:\sin C=3:4:5$
D.若O为△ABC的内心,则△ABC为直角三角形

A.$S_{A}:S_{B}:S_{C}=3:4:5$
B.O有可能是△ABC的重心
C.若O为△ABC的外心,则$\sin A:\sin B:\sin C=3:4:5$
D.若O为△ABC的内心,则△ABC为直角三角形
答案:
7. AD [对于A,由奔驰定理可得,
$3\overrightarrow{OA} + 4\overrightarrow{OB} + 5\overrightarrow{OC} = S_{A}\cdot\overrightarrow{OA} + S_{B}\cdot\overrightarrow{OB} + S_{C}\cdot\overrightarrow{OC} = 0$,
因为$\overrightarrow{OA}$,$\overrightarrow{OB}$,$\overrightarrow{OC}$不共线,
所以$S_{A}:S_{B}:S_{C} = 3:4:5$,
故A正确;
对于B,若$O$是$\triangle ABC$的重心,
则$\overrightarrow{OA} + \overrightarrow{OB} + \overrightarrow{OC} = 0$,
因为$3\overrightarrow{OA} + 4\overrightarrow{OB} + 5\overrightarrow{OC} = 0$,所以$\overrightarrow{OB} = 2\overrightarrow{CO}$,即$O$,$B$,$C$三点共线,故B错误;
对于C,当$O$为$\triangle ABC$的外心时,
$|\overrightarrow{OA}| = |\overrightarrow{OB}| = |\overrightarrow{OC}|$,
所以$S_{A}:S_{B}:S_{C} = \sin\angle BOC:\sin\angle AOC:\sin\angle AOB = 3:4:5$,
即$\sin 2A:\sin 2B:\sin 2C = 3:4:5$,
故C错误;
对于D,当$O$为$\triangle ABC$的内心时,
$S_{A}:S_{B}:S_{C} = \frac{1}{2}ar:\frac{1}{2}br:\frac{1}{2}cr$
$= a:b:c = 3:4:5$($r$为内切圆半径,$a$,$b$,$c$分别为角$A$,$B$,$C$的对边),
所以$a^{2} + b^{2} = c^{2}$,所以$C = \frac{\pi}{2}$,故D正确。]
$3\overrightarrow{OA} + 4\overrightarrow{OB} + 5\overrightarrow{OC} = S_{A}\cdot\overrightarrow{OA} + S_{B}\cdot\overrightarrow{OB} + S_{C}\cdot\overrightarrow{OC} = 0$,
因为$\overrightarrow{OA}$,$\overrightarrow{OB}$,$\overrightarrow{OC}$不共线,
所以$S_{A}:S_{B}:S_{C} = 3:4:5$,
故A正确;
对于B,若$O$是$\triangle ABC$的重心,
则$\overrightarrow{OA} + \overrightarrow{OB} + \overrightarrow{OC} = 0$,
因为$3\overrightarrow{OA} + 4\overrightarrow{OB} + 5\overrightarrow{OC} = 0$,所以$\overrightarrow{OB} = 2\overrightarrow{CO}$,即$O$,$B$,$C$三点共线,故B错误;
对于C,当$O$为$\triangle ABC$的外心时,
$|\overrightarrow{OA}| = |\overrightarrow{OB}| = |\overrightarrow{OC}|$,
所以$S_{A}:S_{B}:S_{C} = \sin\angle BOC:\sin\angle AOC:\sin\angle AOB = 3:4:5$,
即$\sin 2A:\sin 2B:\sin 2C = 3:4:5$,
故C错误;
对于D,当$O$为$\triangle ABC$的内心时,
$S_{A}:S_{B}:S_{C} = \frac{1}{2}ar:\frac{1}{2}br:\frac{1}{2}cr$
$= a:b:c = 3:4:5$($r$为内切圆半径,$a$,$b$,$c$分别为角$A$,$B$,$C$的对边),
所以$a^{2} + b^{2} = c^{2}$,所以$C = \frac{\pi}{2}$,故D正确。]
8.(多选)(2024·重庆模拟)已知点O在△ABC所在的平面内,则以下说法正确的有 ( )
A.若$|\overrightarrow{BC}|\overrightarrow{OA}+|\overrightarrow{AC}|\overrightarrow{OB}+|\overrightarrow{AB}|\overrightarrow{OC}=\boldsymbol{0}$,则点O是△ABC的重心
B.若$\overrightarrow{OA}\cdot(\frac{\overrightarrow{AC}}{|\overrightarrow{AC}|}-\frac{\overrightarrow{AB}}{|\overrightarrow{AB}|})=\overrightarrow{OB}\cdot(\frac{\overrightarrow{BC}}{|\overrightarrow{BC}|}-\frac{\overrightarrow{BA}}{|\overrightarrow{BA}|})=0$,则点O是△ABC的内心
C.若$(\overrightarrow{OA}+\overrightarrow{OB})\cdot\overrightarrow{AB}=(\overrightarrow{OB}+\overrightarrow{OC})\cdot\overrightarrow{BC}=0$,则点O是△ABC的外心
D.若O为△ABC的外心,且$2\overrightarrow{BO}=\overrightarrow{BA}+\overrightarrow{BC}$,则B为△ABC的垂心
A.若$|\overrightarrow{BC}|\overrightarrow{OA}+|\overrightarrow{AC}|\overrightarrow{OB}+|\overrightarrow{AB}|\overrightarrow{OC}=\boldsymbol{0}$,则点O是△ABC的重心
B.若$\overrightarrow{OA}\cdot(\frac{\overrightarrow{AC}}{|\overrightarrow{AC}|}-\frac{\overrightarrow{AB}}{|\overrightarrow{AB}|})=\overrightarrow{OB}\cdot(\frac{\overrightarrow{BC}}{|\overrightarrow{BC}|}-\frac{\overrightarrow{BA}}{|\overrightarrow{BA}|})=0$,则点O是△ABC的内心
C.若$(\overrightarrow{OA}+\overrightarrow{OB})\cdot\overrightarrow{AB}=(\overrightarrow{OB}+\overrightarrow{OC})\cdot\overrightarrow{BC}=0$,则点O是△ABC的外心
D.若O为△ABC的外心,且$2\overrightarrow{BO}=\overrightarrow{BA}+\overrightarrow{BC}$,则B为△ABC的垂心
答案:
8. BCD [对于A,设
$a$,$b$,$c$分别为角
$A$,$B$,$C$的对边,在
$AB$,$AC$上分别取
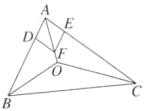
点$D$,$E$,使得$\overrightarrow{AD} = \frac{\overrightarrow{AB}}{c}$,$\overrightarrow{AE} = \frac{\overrightarrow{AC}}{b}$,
则$|\overrightarrow{AD}| = |\overrightarrow{AE}| = 1$,以$AD$,$AE$为邻边作平行四边形$ADFE$,如图所示,
则四边形$ADFE$是菱形,
且$\overrightarrow{AF} = \overrightarrow{AD} + \overrightarrow{AE} = \frac{\overrightarrow{AB}}{c} + \frac{\overrightarrow{AC}}{b}$,
所以$AF$平分$\angle BAC$,
因为$|\overrightarrow{BC}|\overrightarrow{OA} + |\overrightarrow{AC}|\overrightarrow{OB} + |\overrightarrow{AB}|\overrightarrow{OC} = 0$,
即$a\overrightarrow{OA} + b\overrightarrow{OB} + c\overrightarrow{OC} = 0$,
所以$a\cdot\overrightarrow{OA} + b\cdot(\overrightarrow{OA} + \overrightarrow{AB}) + c(\overrightarrow{OA} + \overrightarrow{AC}) = 0$,
即$(a + b + c)\overrightarrow{OA} + b\overrightarrow{AB} + c\overrightarrow{AC} = 0$,
所以$\overrightarrow{AO} = \frac{b}{a + b + c}\overrightarrow{AB} + \frac{c}{a + b + c}\overrightarrow{AC}$
$= \frac{bc}{a + b + c}(\frac{\overrightarrow{AB}}{c} + \frac{\overrightarrow{AC}}{b})$
$= \frac{bc}{a + b + c}\overrightarrow{AF}$,
所以$A$,$O$,$F$三点共线,即$O$在$\angle BAC$的平分线上,
同理可得$O$在其他两角的平分线上,
所以$O$为$\triangle ABC$的内心,故A错误;
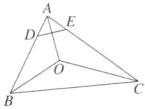
对于B,在$AB$,$AC$
上分别取点$D$,$E$,
使得$\overrightarrow{AE} = \frac{\overrightarrow{AC}}{|\overrightarrow{AC}|}$,
$\overrightarrow{AD} = \frac{\overrightarrow{AB}}{|\overrightarrow{AB}|}$,
如图,
则$|\overrightarrow{AD}| = |\overrightarrow{AE}| = 1$,
且$\frac{\overrightarrow{AC}}{|\overrightarrow{AC}|} - \frac{\overrightarrow{AB}}{|\overrightarrow{AB}|} = \overrightarrow{DE}$,
因为$\overrightarrow{OA}\cdot(\frac{\overrightarrow{AC}}{|\overrightarrow{AC}|} - \frac{\overrightarrow{AB}}{|\overrightarrow{AB}|}) = 0$,
即$\overrightarrow{OA}\perp\overrightarrow{DE}$,又$|\overrightarrow{AD}| = |\overrightarrow{AE}| = 1$知,
$AO$平分$\angle BAC$,
同理,可得$BO$平分$\angle ABC$,故$O$为$\triangle ABC$的内心,故B正确;
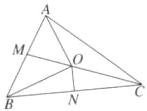
对于C,取$AB$,$BC$的中点分别为$M$,$N$,如图,
因为$(\overrightarrow{OA} + \overrightarrow{OB})\cdot\overrightarrow{AB} = (\overrightarrow{OB} + \overrightarrow{OC})\cdot\overrightarrow{BC} = 0$,
所以$2\overrightarrow{OM}\cdot\overrightarrow{AB} = 2\overrightarrow{ON}\cdot\overrightarrow{BC} = 0$,
即$OM\perp AB$,$ON\perp BC$,所以$O$是$\triangle ABC$的外心,故C正确;
对于D,因为$2\overrightarrow{BO} = \overrightarrow{BA} + \overrightarrow{BC}$,
所以$\overrightarrow{OA} = -\overrightarrow{OC}$,即$O$为$AC$的中点,又$O$为$\triangle ABC$的外心,
所以$\angle B = 90^{\circ}$,则$B$为$\triangle ABC$的垂心,故D正确。
]
8. BCD [对于A,设
$a$,$b$,$c$分别为角
$A$,$B$,$C$的对边,在
$AB$,$AC$上分别取
点$D$,$E$,使得$\overrightarrow{AD} = \frac{\overrightarrow{AB}}{c}$,$\overrightarrow{AE} = \frac{\overrightarrow{AC}}{b}$,
则$|\overrightarrow{AD}| = |\overrightarrow{AE}| = 1$,以$AD$,$AE$为邻边作平行四边形$ADFE$,如图所示,
则四边形$ADFE$是菱形,
且$\overrightarrow{AF} = \overrightarrow{AD} + \overrightarrow{AE} = \frac{\overrightarrow{AB}}{c} + \frac{\overrightarrow{AC}}{b}$,
所以$AF$平分$\angle BAC$,
因为$|\overrightarrow{BC}|\overrightarrow{OA} + |\overrightarrow{AC}|\overrightarrow{OB} + |\overrightarrow{AB}|\overrightarrow{OC} = 0$,
即$a\overrightarrow{OA} + b\overrightarrow{OB} + c\overrightarrow{OC} = 0$,
所以$a\cdot\overrightarrow{OA} + b\cdot(\overrightarrow{OA} + \overrightarrow{AB}) + c(\overrightarrow{OA} + \overrightarrow{AC}) = 0$,
即$(a + b + c)\overrightarrow{OA} + b\overrightarrow{AB} + c\overrightarrow{AC} = 0$,
所以$\overrightarrow{AO} = \frac{b}{a + b + c}\overrightarrow{AB} + \frac{c}{a + b + c}\overrightarrow{AC}$
$= \frac{bc}{a + b + c}(\frac{\overrightarrow{AB}}{c} + \frac{\overrightarrow{AC}}{b})$
$= \frac{bc}{a + b + c}\overrightarrow{AF}$,
所以$A$,$O$,$F$三点共线,即$O$在$\angle BAC$的平分线上,
同理可得$O$在其他两角的平分线上,
所以$O$为$\triangle ABC$的内心,故A错误;
对于B,在$AB$,$AC$
上分别取点$D$,$E$,
使得$\overrightarrow{AE} = \frac{\overrightarrow{AC}}{|\overrightarrow{AC}|}$,
$\overrightarrow{AD} = \frac{\overrightarrow{AB}}{|\overrightarrow{AB}|}$,
如图,
则$|\overrightarrow{AD}| = |\overrightarrow{AE}| = 1$,
且$\frac{\overrightarrow{AC}}{|\overrightarrow{AC}|} - \frac{\overrightarrow{AB}}{|\overrightarrow{AB}|} = \overrightarrow{DE}$,
因为$\overrightarrow{OA}\cdot(\frac{\overrightarrow{AC}}{|\overrightarrow{AC}|} - \frac{\overrightarrow{AB}}{|\overrightarrow{AB}|}) = 0$,
即$\overrightarrow{OA}\perp\overrightarrow{DE}$,又$|\overrightarrow{AD}| = |\overrightarrow{AE}| = 1$知,
$AO$平分$\angle BAC$,
同理,可得$BO$平分$\angle ABC$,故$O$为$\triangle ABC$的内心,故B正确;
对于C,取$AB$,$BC$的中点分别为$M$,$N$,如图,
因为$(\overrightarrow{OA} + \overrightarrow{OB})\cdot\overrightarrow{AB} = (\overrightarrow{OB} + \overrightarrow{OC})\cdot\overrightarrow{BC} = 0$,
所以$2\overrightarrow{OM}\cdot\overrightarrow{AB} = 2\overrightarrow{ON}\cdot\overrightarrow{BC} = 0$,
即$OM\perp AB$,$ON\perp BC$,所以$O$是$\triangle ABC$的外心,故C正确;
对于D,因为$2\overrightarrow{BO} = \overrightarrow{BA} + \overrightarrow{BC}$,
所以$\overrightarrow{OA} = -\overrightarrow{OC}$,即$O$为$AC$的中点,又$O$为$\triangle ABC$的外心,
所以$\angle B = 90^{\circ}$,则$B$为$\triangle ABC$的垂心,故D正确。



]
9.已知在△ABC中,G是重心,内角A,B,C的对边分别为a,b,c,且$56a\overrightarrow{GA}+40b\overrightarrow{GB}+35c\overrightarrow{GC}=\boldsymbol{0}$,则B = ________.
答案:
9. $\frac{\pi}{3}$
10.设点P在△ABC内部且为△ABC的外心,∠BAC = $\frac{\pi}{6}$,如图.若△PBC,△PCA,△PAB的面积分别为$\frac{1}{2}$,x,y,则x + y的最大值是_______.


答案:
10. $\frac{\sqrt{3}}{3}$
解析 方法一 据奔驰定理得,
$\frac{1}{2}\overrightarrow{PA} + x\overrightarrow{PB} + y\overrightarrow{PC} = 0$,
即$\overrightarrow{AP} = 2x\overrightarrow{PB} + 2y\overrightarrow{PC}$,$x > 0$,$y > 0$,
平方得$\overrightarrow{AP}^{2} = 4x^{2}\overrightarrow{PB}^{2} + 4y^{2}\overrightarrow{PC}^{2} + 8xy|\overrightarrow{PB}|\cdot|\overrightarrow{PC}|\cdot\cos\angle BPC$,
又因为点$P$是$\triangle ABC$的外心,
$\angle BAC = \frac{\pi}{6}$,
所以$|\overrightarrow{PA}| = |\overrightarrow{PB}| = |\overrightarrow{PC}|$,
且$\angle BPC = 2\angle BAC = \frac{\pi}{3}$,
所以$x^{2} + y^{2} + xy = \frac{1}{4}$,
$(x + y)^{2} = \frac{1}{4} + xy\leqslant\frac{1}{4} + (\frac{x + y}{2})^{2}$,
解得$x + y\leqslant\frac{\sqrt{3}}{3}$,当且仅当$x = y = \frac{\sqrt{3}}{6}$时取等号,所以$(x + y)_{\max} = \frac{\sqrt{3}}{3}$。
方法二 因为点$P$是$\triangle ABC$的外心,
所以$S_{\triangle PBC}:S_{\triangle PCA}:S_{\triangle PAB} = \sin 2A:\sin 2B:\sin 2C$
$= \frac{1}{2}:x:y$,$x > 0$,$y > 0$,
又$\angle BAC = \frac{\pi}{6}$,$\therefore \sin 2A = \frac{\sqrt{3}}{2}$,
$\therefore x = \frac{\sqrt{3}}{3}\sin 2B$,$y = \frac{\sqrt{3}}{3}\sin 2C$,
$\therefore x + y = \frac{\sqrt{3}}{3}(\sin 2B + \sin 2C)$
$= \frac{\sqrt{3}}{3}[\sin 2B + \sin(\frac{5\pi}{3} - 2B)]$
$= \frac{\sqrt{3}}{3}\sin(2B - \frac{\pi}{3})$,
又$\because B\in(0,\frac{5\pi}{6})$,
$\therefore 2B - \frac{\pi}{3}\in(-\frac{\pi}{3},\frac{4\pi}{3})$,
$\therefore \sin(2B - \frac{\pi}{3})\in(-\frac{\sqrt{3}}{2},1]$,
$\therefore x + y\in(0,\frac{\sqrt{3}}{3}]$,
$\therefore (x + y)_{\max} = \frac{\sqrt{3}}{3}$。
解析 方法一 据奔驰定理得,
$\frac{1}{2}\overrightarrow{PA} + x\overrightarrow{PB} + y\overrightarrow{PC} = 0$,
即$\overrightarrow{AP} = 2x\overrightarrow{PB} + 2y\overrightarrow{PC}$,$x > 0$,$y > 0$,
平方得$\overrightarrow{AP}^{2} = 4x^{2}\overrightarrow{PB}^{2} + 4y^{2}\overrightarrow{PC}^{2} + 8xy|\overrightarrow{PB}|\cdot|\overrightarrow{PC}|\cdot\cos\angle BPC$,
又因为点$P$是$\triangle ABC$的外心,
$\angle BAC = \frac{\pi}{6}$,
所以$|\overrightarrow{PA}| = |\overrightarrow{PB}| = |\overrightarrow{PC}|$,
且$\angle BPC = 2\angle BAC = \frac{\pi}{3}$,
所以$x^{2} + y^{2} + xy = \frac{1}{4}$,
$(x + y)^{2} = \frac{1}{4} + xy\leqslant\frac{1}{4} + (\frac{x + y}{2})^{2}$,
解得$x + y\leqslant\frac{\sqrt{3}}{3}$,当且仅当$x = y = \frac{\sqrt{3}}{6}$时取等号,所以$(x + y)_{\max} = \frac{\sqrt{3}}{3}$。
方法二 因为点$P$是$\triangle ABC$的外心,
所以$S_{\triangle PBC}:S_{\triangle PCA}:S_{\triangle PAB} = \sin 2A:\sin 2B:\sin 2C$
$= \frac{1}{2}:x:y$,$x > 0$,$y > 0$,
又$\angle BAC = \frac{\pi}{6}$,$\therefore \sin 2A = \frac{\sqrt{3}}{2}$,
$\therefore x = \frac{\sqrt{3}}{3}\sin 2B$,$y = \frac{\sqrt{3}}{3}\sin 2C$,
$\therefore x + y = \frac{\sqrt{3}}{3}(\sin 2B + \sin 2C)$
$= \frac{\sqrt{3}}{3}[\sin 2B + \sin(\frac{5\pi}{3} - 2B)]$
$= \frac{\sqrt{3}}{3}\sin(2B - \frac{\pi}{3})$,
又$\because B\in(0,\frac{5\pi}{6})$,
$\therefore 2B - \frac{\pi}{3}\in(-\frac{\pi}{3},\frac{4\pi}{3})$,
$\therefore \sin(2B - \frac{\pi}{3})\in(-\frac{\sqrt{3}}{2},1]$,
$\therefore x + y\in(0,\frac{\sqrt{3}}{3}]$,
$\therefore (x + y)_{\max} = \frac{\sqrt{3}}{3}$。
查看更多完整答案,请扫码查看


