2025年步步高大二轮专题复习高中数学
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年步步高大二轮专题复习高中数学 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第40页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
跟踪演练3 (1)已知对任意平面向量$\overrightarrow{AB}=(x,$y),把$\overrightarrow{AB}$绕其起点沿逆时针方向旋转θ角得到向量$\overrightarrow{AP}=(xcosθ - ysinθ,$xsinθ + ycosθ),叫做把点B绕点A沿逆时针方向旋转θ角得到点P.已知平面内点A(1,2),点$B(1 + \sqrt{3},$4),把点B绕点A沿顺时针方向旋转$\frac{π}{3}$后得到点P,则点P的坐标为 ( )
$A. (\frac{3\sqrt{3}}{2}+1,$$\frac{3}{2}) B. ( - \frac{3\sqrt{3}}{2}+1,$$\frac{3}{2})$
$C. (\frac{5}{2},$$\frac{3\sqrt{3}}{2}) D. (\frac{5}{2},$$\frac{1}{2})$
$A. (\frac{3\sqrt{3}}{2}+1,$$\frac{3}{2}) B. ( - \frac{3\sqrt{3}}{2}+1,$$\frac{3}{2})$
$C. (\frac{5}{2},$$\frac{3\sqrt{3}}{2}) D. (\frac{5}{2},$$\frac{1}{2})$
答案:
(1)A
(1)A
(2)对于非零向量α,β,定义一种运算:$α°β=\frac{α·β}{β·β},$已知非零向量a,b的夹角$θ∈(\frac{π}{4},$$\frac{π}{2}),$且a°b,b°a都在集合${\frac{n}{2}|n∈N}$中,则a°b等于 ( )
$A. \frac{5}{2}$或$\frac{3}{2} B. \frac{1}{2}$或$\frac{3}{2}$
$C. 1 D. \frac{1}{2}$
$A. \frac{5}{2}$或$\frac{3}{2} B. \frac{1}{2}$或$\frac{3}{2}$
$C. 1 D. \frac{1}{2}$
答案:
(2)D
(2)D
1. 对于非零向量a,b,定义a⊕b = a·b·tan〈a,b〉.若$a⊕b = |a + b|=\sqrt{3}|a - b|=\sqrt{3},$则tan〈a,b〉等于 ( )
$A. \frac{2\sqrt{3}}{3} B. \sqrt{2} C. 2\sqrt{3} D. 3\sqrt{2}$
$A. \frac{2\sqrt{3}}{3} B. \sqrt{2} C. 2\sqrt{3} D. 3\sqrt{2}$
答案:
C
2. 若向量a=(x₁,y₁),b=(x₂,y₂),则a,b构成的平行四边形的面积S可以用a,b的外积a×b表示出来,即S = |a×b| = |x₁y₂ - x₂y₁|.已知在平面直角坐标系Oxy中,点A(cosα,$\sqrt{3}),$B(sin2α,2cosα),α∈[0,$\frac{π}{2}],$则△OAB面积的最大值为 ( )
$A. 1 B. \sqrt{2} C. 2 D. 3$
$A. 1 B. \sqrt{2} C. 2 D. 3$
答案:
A
3. (多选)如图所示,设Ox,Oy是平面内相交成$θ(θ≠\frac{π}{2})$角的两条数轴, e₁,e₂分别是与x,y轴正方向同向的单位向量,则称平面坐标系Oxy为θ反射坐标系,若$\overrightarrow{OM}=xe₁ + ye₂,$则把有序数对(x,y)叫做向量$\overrightarrow{OM}$的反射坐标,记为$\overrightarrow{OM}=(x,$y),在$θ=\frac{2π}{3}$的反射坐标系中,a=(1,2),b=(2, - 1),则下列结论中,正确的是 ( )
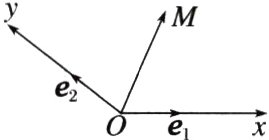
A. a - b=( - 1,3)
$B. |a|=\sqrt{5}$
C. a⊥b
D. a在b上的投影向量的长度为$ - \frac{3\sqrt{7}}{14}$

A. a - b=( - 1,3)
$B. |a|=\sqrt{5}$
C. a⊥b
D. a在b上的投影向量的长度为$ - \frac{3\sqrt{7}}{14}$
答案:
AD
4. (多选)现在给出一个向量的新运算a×b,叫作向量a与b的外积,它是一个满足如下两个条件的向量:
①a·(a×b)=0,b·(a×b)=0,且{a,b,a×b}构成右手系的基(即三个向量的方向依次与右手的拇指、食指、中指的指向一致,如图1所示);②向量a×b的模|a×b| = |a||b|sin〈a,b〉.如图2,在棱长为2的正四面体ABCD中,下列说法正确的是 ( )


$A. \overrightarrow{AB}×\overrightarrow{AC}=\overrightarrow{AC}×\overrightarrow{AB}$
$B. 4|\overrightarrow{BC}×\overrightarrow{AC}|$与正四面体的表面积相等
$C. (\overrightarrow{AC}×\overrightarrow{AB})·\overrightarrow{AD}=4\sqrt{2}$
$D. |(\overrightarrow{AC}×\overrightarrow{AB})×\overrightarrow{AD}| = |\overrightarrow{AC}×(\overrightarrow{AB}×\overrightarrow{AD})|$
①a·(a×b)=0,b·(a×b)=0,且{a,b,a×b}构成右手系的基(即三个向量的方向依次与右手的拇指、食指、中指的指向一致,如图1所示);②向量a×b的模|a×b| = |a||b|sin〈a,b〉.如图2,在棱长为2的正四面体ABCD中,下列说法正确的是 ( )


$A. \overrightarrow{AB}×\overrightarrow{AC}=\overrightarrow{AC}×\overrightarrow{AB}$
$B. 4|\overrightarrow{BC}×\overrightarrow{AC}|$与正四面体的表面积相等
$C. (\overrightarrow{AC}×\overrightarrow{AB})·\overrightarrow{AD}=4\sqrt{2}$
$D. |(\overrightarrow{AC}×\overrightarrow{AB})×\overrightarrow{AD}| = |\overrightarrow{AC}×(\overrightarrow{AB}×\overrightarrow{AD})|$
答案:
CD [对于A,易得$\vert \overrightarrow{AB}\times \overrightarrow{AC}\vert =\vert \overrightarrow{AC}\times \overrightarrow{AB}\vert$,根据右手系的基的定义,拇指指向$\overrightarrow{AB}$的方向,食指指向$\overrightarrow{AC}$的方向,则中指指向$\overrightarrow{AB}\times \overrightarrow{AC}$的方向,其垂直于平面$ABC$,方向向下,同理得$\overrightarrow{AC}\times \overrightarrow{AB}$垂直于平面$ABC$,方向向上,所以$\overrightarrow{AB}\times \overrightarrow{AC}$与$\overrightarrow{AC}\times \overrightarrow{AB}$两向量大小相同,方向相反,A错误;
对于B,$4\vert \overrightarrow{BC}\times \overrightarrow{AC}\vert =4\vert \overrightarrow{BC}\vert \vert \overrightarrow{AC}\vert \sin \frac{\pi}{3}=4\times 2\times 2\times \frac{\sqrt{3}}{2}=8\sqrt{3}$,正四面体的表面积为$4\times \frac{1}{2}\times \vert \overrightarrow{BC}\vert \vert \overrightarrow{AC}\vert \times \sin \frac{\pi}{3}=4\sqrt{3}$,B错误;
对于C,设$\overrightarrow{AC}\times \overrightarrow{AB}=\overrightarrow{AM}$,由A选项知$\overrightarrow{AM}$垂直于平面$ABC$,方向向上,$\vert \overrightarrow{AM}\vert =\vert \overrightarrow{AB}\vert \vert \overrightarrow{AC}\vert \sin \frac{\pi}{3}=2\sqrt{3}$,
所以$(\overrightarrow{AC}\times \overrightarrow{AB})\cdot \overrightarrow{AD}=\overrightarrow{AM}\cdot \overrightarrow{AD}=\vert \overrightarrow{AM}\vert \vert \overrightarrow{AD}\vert \cos \langle \overrightarrow{AM},\overrightarrow{AD}\rangle =4\sqrt{3}\cos \langle \overrightarrow{AM},\overrightarrow{AD}\rangle$。
如图,过点$A$作$AE\perp BC$于点$E$,过点$D$作$DF\perp AE$于点$F$,
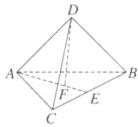
则$FD$是正四面体$ABCD$的高,$\overrightarrow{AM}$与$\overrightarrow{FD}$共线,$\langle \overrightarrow{AM},\overrightarrow{AD}\rangle =\angle ADF$。
由$\frac{1}{3}\times FD\times \frac{1}{2}\times AB\times AC\times \sin \frac{\pi}{3}=\frac{\sqrt{2}}{12}\times {2}^{3}$,得$FD=\frac{2\sqrt{6}}{3}$,
所以$\cos \langle \overrightarrow{AM},\overrightarrow{AD}\rangle =\frac{FD}{AD}=\frac{\sqrt{6}}{3}$,
所以$(\overrightarrow{AC}\times \overrightarrow{AB})\cdot \overrightarrow{AD}=4\sqrt{3}\times \frac{\sqrt{6}}{3}=4\sqrt{2}$,C正确;
对于D,$\vert (\overrightarrow{AC}\times \overrightarrow{AB})\times \overrightarrow{AD}\vert =\vert \overrightarrow{AC}\times \overrightarrow{AB}\vert \vert \overrightarrow{AD}\vert \sin \langle (\overrightarrow{AC}\times \overrightarrow{AB}),\overrightarrow{AD}\rangle$,
$\vert \overrightarrow{AC}\times (\overrightarrow{AB}\times \overrightarrow{AD})\vert =\vert \overrightarrow{AC}\vert \vert \overrightarrow{AB}\times \overrightarrow{AD}\vert \sin \langle \overrightarrow{AC},(\overrightarrow{AB}\times \overrightarrow{AD})\rangle$,
易知$\vert \overrightarrow{AC}\times \overrightarrow{AB}\vert =\vert \overrightarrow{AB}\times \overrightarrow{AD}\vert$,$\vert \overrightarrow{AD}\vert =\vert \overrightarrow{AC}\vert$,
$\sin \langle (\overrightarrow{AC}\times \overrightarrow{AB}),\overrightarrow{AD}\rangle =\sin \langle \overrightarrow{AC},(\overrightarrow{AB}\times \overrightarrow{AD})\rangle$,
所以$\vert (\overrightarrow{AC}\times \overrightarrow{AB})\times \overrightarrow{AD}\vert =\vert \overrightarrow{AC}\times (\overrightarrow{AB}\times \overrightarrow{AD})\vert$,D正确。]
CD [对于A,易得$\vert \overrightarrow{AB}\times \overrightarrow{AC}\vert =\vert \overrightarrow{AC}\times \overrightarrow{AB}\vert$,根据右手系的基的定义,拇指指向$\overrightarrow{AB}$的方向,食指指向$\overrightarrow{AC}$的方向,则中指指向$\overrightarrow{AB}\times \overrightarrow{AC}$的方向,其垂直于平面$ABC$,方向向下,同理得$\overrightarrow{AC}\times \overrightarrow{AB}$垂直于平面$ABC$,方向向上,所以$\overrightarrow{AB}\times \overrightarrow{AC}$与$\overrightarrow{AC}\times \overrightarrow{AB}$两向量大小相同,方向相反,A错误;
对于B,$4\vert \overrightarrow{BC}\times \overrightarrow{AC}\vert =4\vert \overrightarrow{BC}\vert \vert \overrightarrow{AC}\vert \sin \frac{\pi}{3}=4\times 2\times 2\times \frac{\sqrt{3}}{2}=8\sqrt{3}$,正四面体的表面积为$4\times \frac{1}{2}\times \vert \overrightarrow{BC}\vert \vert \overrightarrow{AC}\vert \times \sin \frac{\pi}{3}=4\sqrt{3}$,B错误;
对于C,设$\overrightarrow{AC}\times \overrightarrow{AB}=\overrightarrow{AM}$,由A选项知$\overrightarrow{AM}$垂直于平面$ABC$,方向向上,$\vert \overrightarrow{AM}\vert =\vert \overrightarrow{AB}\vert \vert \overrightarrow{AC}\vert \sin \frac{\pi}{3}=2\sqrt{3}$,
所以$(\overrightarrow{AC}\times \overrightarrow{AB})\cdot \overrightarrow{AD}=\overrightarrow{AM}\cdot \overrightarrow{AD}=\vert \overrightarrow{AM}\vert \vert \overrightarrow{AD}\vert \cos \langle \overrightarrow{AM},\overrightarrow{AD}\rangle =4\sqrt{3}\cos \langle \overrightarrow{AM},\overrightarrow{AD}\rangle$。
如图,过点$A$作$AE\perp BC$于点$E$,过点$D$作$DF\perp AE$于点$F$,

则$FD$是正四面体$ABCD$的高,$\overrightarrow{AM}$与$\overrightarrow{FD}$共线,$\langle \overrightarrow{AM},\overrightarrow{AD}\rangle =\angle ADF$。
由$\frac{1}{3}\times FD\times \frac{1}{2}\times AB\times AC\times \sin \frac{\pi}{3}=\frac{\sqrt{2}}{12}\times {2}^{3}$,得$FD=\frac{2\sqrt{6}}{3}$,
所以$\cos \langle \overrightarrow{AM},\overrightarrow{AD}\rangle =\frac{FD}{AD}=\frac{\sqrt{6}}{3}$,
所以$(\overrightarrow{AC}\times \overrightarrow{AB})\cdot \overrightarrow{AD}=4\sqrt{3}\times \frac{\sqrt{6}}{3}=4\sqrt{2}$,C正确;
对于D,$\vert (\overrightarrow{AC}\times \overrightarrow{AB})\times \overrightarrow{AD}\vert =\vert \overrightarrow{AC}\times \overrightarrow{AB}\vert \vert \overrightarrow{AD}\vert \sin \langle (\overrightarrow{AC}\times \overrightarrow{AB}),\overrightarrow{AD}\rangle$,
$\vert \overrightarrow{AC}\times (\overrightarrow{AB}\times \overrightarrow{AD})\vert =\vert \overrightarrow{AC}\vert \vert \overrightarrow{AB}\times \overrightarrow{AD}\vert \sin \langle \overrightarrow{AC},(\overrightarrow{AB}\times \overrightarrow{AD})\rangle$,
易知$\vert \overrightarrow{AC}\times \overrightarrow{AB}\vert =\vert \overrightarrow{AB}\times \overrightarrow{AD}\vert$,$\vert \overrightarrow{AD}\vert =\vert \overrightarrow{AC}\vert$,
$\sin \langle (\overrightarrow{AC}\times \overrightarrow{AB}),\overrightarrow{AD}\rangle =\sin \langle \overrightarrow{AC},(\overrightarrow{AB}\times \overrightarrow{AD})\rangle$,
所以$\vert (\overrightarrow{AC}\times \overrightarrow{AB})\times \overrightarrow{AD}\vert =\vert \overrightarrow{AC}\times (\overrightarrow{AB}\times \overrightarrow{AD})\vert$,D正确。]
5. 给出定义:对于向量b=(sinx,cosx),若函数f(x)=a·b,则称向量a为函数f(x)的伴随向量,同时称函数f(x)为向量a的伴随函数.
已知A( - 1,$\frac{3}{2}),$B(1,3),函数h(x)的伴随向量为n=(0,1),点P为函数h(x)的图象上一点,满足$|\overrightarrow{AP}+\overrightarrow{BP}| = |\overrightarrow{AB}|,$则点P的坐标为________.
已知A( - 1,$\frac{3}{2}),$B(1,3),函数h(x)的伴随向量为n=(0,1),点P为函数h(x)的图象上一点,满足$|\overrightarrow{AP}+\overrightarrow{BP}| = |\overrightarrow{AB}|,$则点P的坐标为________.
答案:
(0,1)
6. (2024·邯郸模拟)对任意两个非零的平面向量a和b,定义:$a⊕b=\frac{a·b}{|a|² + |b|²},$$a⊙b=\frac{a·b}{|b|²}.$若平面向量a,b满足|a| > |b| > 0,且a⊕b和a⊙b都在集合${\frac{n}{4}|n∈Z,0 < n≤4}$中,则a⊕b + a⊙b = __________.
答案:
1或$\frac{5}{4}$
解析 因为$\{\frac{n}{4}\vert n\in Z,0\lt n\leqslant 4\}=\{\frac{1}{4},\frac{1}{2},\frac{3}{4},1\}$,设向量$a$和$b$的夹角为$\theta$,
因为$\vert a\vert > \vert b\vert > 0$,所以$\vert a{\vert }^{2}+\vert b{\vert }^{2}> 2\vert a\vert \vert b\vert$,
得到$a\oplus b=\frac{a\cdot b}{\vert a{\vert }^{2}+\vert b{\vert }^{2}}=\frac{\vert a\vert \vert b\vert \cos \theta }{\vert a{\vert }^{2}+\vert b{\vert }^{2}}<\frac{\vert a\vert \vert b\vert \cos \theta }{2\vert a\vert \vert b\vert }=\frac{\cos \theta }{2}$,
又$\theta \in [0,\pi ]$,所以$\frac{\cos \theta }{2}\leqslant \frac{1}{2}$,
所以$a\oplus b<\frac{1}{2}$,又$a\oplus b$在集合$\{\frac{n}{4}\vert n\in Z,0\lt n\leqslant 4\}$中,所以$a\oplus b=\frac{1}{4}$,
所以$\frac{\cos \theta }{2}> \frac{1}{4}$,即$\cos \theta > \frac{1}{2}$;
又因为$a\odot b=\frac{a\cdot b}{\vert b{\vert }^{2}}=\frac{\vert a\vert \vert b\vert \cos \theta }{\vert b{\vert }^{2}}=\frac{\vert a\vert }{\vert b\vert }\cos \theta > \cos \theta > \frac{1}{2}$,
所以$a\odot b=\frac{3}{4}$或1,
所以$a\oplus b + a\odot b = 1$或$\frac{5}{4}$。
解析 因为$\{\frac{n}{4}\vert n\in Z,0\lt n\leqslant 4\}=\{\frac{1}{4},\frac{1}{2},\frac{3}{4},1\}$,设向量$a$和$b$的夹角为$\theta$,
因为$\vert a\vert > \vert b\vert > 0$,所以$\vert a{\vert }^{2}+\vert b{\vert }^{2}> 2\vert a\vert \vert b\vert$,
得到$a\oplus b=\frac{a\cdot b}{\vert a{\vert }^{2}+\vert b{\vert }^{2}}=\frac{\vert a\vert \vert b\vert \cos \theta }{\vert a{\vert }^{2}+\vert b{\vert }^{2}}<\frac{\vert a\vert \vert b\vert \cos \theta }{2\vert a\vert \vert b\vert }=\frac{\cos \theta }{2}$,
又$\theta \in [0,\pi ]$,所以$\frac{\cos \theta }{2}\leqslant \frac{1}{2}$,
所以$a\oplus b<\frac{1}{2}$,又$a\oplus b$在集合$\{\frac{n}{4}\vert n\in Z,0\lt n\leqslant 4\}$中,所以$a\oplus b=\frac{1}{4}$,
所以$\frac{\cos \theta }{2}> \frac{1}{4}$,即$\cos \theta > \frac{1}{2}$;
又因为$a\odot b=\frac{a\cdot b}{\vert b{\vert }^{2}}=\frac{\vert a\vert \vert b\vert \cos \theta }{\vert b{\vert }^{2}}=\frac{\vert a\vert }{\vert b\vert }\cos \theta > \cos \theta > \frac{1}{2}$,
所以$a\odot b=\frac{3}{4}$或1,
所以$a\oplus b + a\odot b = 1$或$\frac{5}{4}$。
查看更多完整答案,请扫码查看


