第9页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
9. 新趋势 创新实验(2023·河北)物理兴趣小组的同学在实验室测量物体的密度.
Ⅰ. 小明选取适量某种相同的实心小球进行如下实验.
(1)将托盘天平放置在水平台面上,游码放到标尺左端的___________,静止时指针偏右,应向_______调节平衡螺母,直到指针指在分度盘中央.
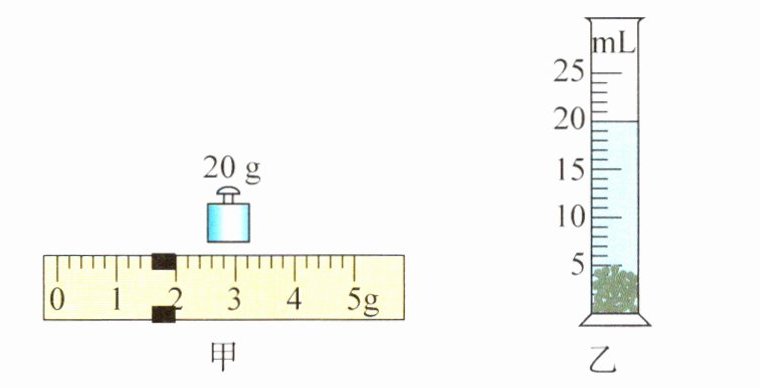
(2)把80个这种小球放在左盘中,向右盘加减砝码,并调节游码在标尺上的位置,直到横梁水平平衡,此时盘中的砝码和游码的位置如图甲所示,则这些小球的总质量为_______g.
(3)向量筒中加入体积为15 mL的水,然后向水中逐个缓慢投入小球,水不溅出,小球沉入水底. 投入50个小球时量筒中液面达到的位置如图乙所示,这些小球的总体积为_______cm³.
(4)根据测量结果可知,这种小球的密度为_______g/cm³.
Ⅱ. 小红采用了如下方法测量另一种外形相同的实心小球的密度.
(1)调节托盘天平平衡后,左盘放适量小球,右盘放烧杯并往其中加水,直至天平平衡.
(2)左盘中减少$n_{1}$个小球,从烧杯中逐渐取水倒入空量筒中,天平恢复平衡时,量筒中液面到达的位置对应的刻度值为$V_{1}$.
(3)向量筒中逐个缓慢投入小球,水不溅出,小球全部浸没在量筒内的水中. 投入$n_{2}$个小球时量筒中液面到达的位置对应的刻度值为$V_{2}$.
(4)已知水的密度为$\rho_{水}$,则小球的密度$\rho=$_______(用$\rho_{水}、V_{1}、V_{2}、n_{1}、n_{2}$表示).
Ⅰ. 小明选取适量某种相同的实心小球进行如下实验.

(1)将托盘天平放置在水平台面上,游码放到标尺左端的___________,静止时指针偏右,应向_______调节平衡螺母,直到指针指在分度盘中央.
(2)把80个这种小球放在左盘中,向右盘加减砝码,并调节游码在标尺上的位置,直到横梁水平平衡,此时盘中的砝码和游码的位置如图甲所示,则这些小球的总质量为_______g.
(3)向量筒中加入体积为15 mL的水,然后向水中逐个缓慢投入小球,水不溅出,小球沉入水底. 投入50个小球时量筒中液面达到的位置如图乙所示,这些小球的总体积为_______cm³.
(4)根据测量结果可知,这种小球的密度为_______g/cm³.
Ⅱ. 小红采用了如下方法测量另一种外形相同的实心小球的密度.
(1)调节托盘天平平衡后,左盘放适量小球,右盘放烧杯并往其中加水,直至天平平衡.
(2)左盘中减少$n_{1}$个小球,从烧杯中逐渐取水倒入空量筒中,天平恢复平衡时,量筒中液面到达的位置对应的刻度值为$V_{1}$.
(3)向量筒中逐个缓慢投入小球,水不溅出,小球全部浸没在量筒内的水中. 投入$n_{2}$个小球时量筒中液面到达的位置对应的刻度值为$V_{2}$.
(4)已知水的密度为$\rho_{水}$,则小球的密度$\rho=$_______(用$\rho_{水}、V_{1}、V_{2}、n_{1}、n_{2}$表示).
答案:
Ⅰ.(1)零刻度线处 左 (2)21.6 (3)5 (4)2.7 Ⅱ.(4)$\frac{n_{2}\rho_{水}V_{1}}{n_{1}(V_{2}-V_{1})}$ 解析:Ⅰ.(1)称量物体质量前,游码应移到标尺左端的零刻度线处,静止时指针偏右,则应向左调节平衡螺母,使天平平衡。(2)由图甲可知,这些小球的总质量$m_{总}=20\ g + 1.6\ g = 21.6\ g$。(3)由图乙可知,50 个小球的总体积为$20\ mL - 15\ mL = 5\ mL = 5\ cm^{3}$。(4)一个小球的体积为$\frac{5\ cm^{3}}{50}=0.1\ cm^{3}$,80 个小球的总体积$V = 0.1\ cm^{3}×80 = 8\ cm^{3}$,则这种小球的密度$\rho=\frac{m_{总}}{V}=\frac{21.6\ g}{8\ cm^{3}} = 2.7\ g/cm^{3}$。
Ⅱ.(4)由题意可知,$n_{1}$个小球的总质量等于体积为$V_{1}$的水的质量,即$m_{总}=m_{水}=\rho_{水}V_{1}$,则一个小球的质量$m_{0}=\frac{m_{总}}{n_{1}}=\frac{\rho_{水}V_{1}}{n_{1}}$,$n_{2}$个小球的总体积$V_{总}=V_{2}-V_{1}$,则一个小球的体积$V_{0}=\frac{V_{总}}{n_{2}}=\frac{V_{2}-V_{1}}{n_{2}}$,所以小球的密度$\rho=\frac{m_{0}}{V_{0}}=\frac{\frac{\rho_{水}V_{1}}{n_{1}}}{\frac{V_{2}-V_{1}}{n_{2}}}=\frac{n_{2}\rho_{水}V_{1}}{n_{1}(V_{2}-V_{1})}$。
Ⅱ.(4)由题意可知,$n_{1}$个小球的总质量等于体积为$V_{1}$的水的质量,即$m_{总}=m_{水}=\rho_{水}V_{1}$,则一个小球的质量$m_{0}=\frac{m_{总}}{n_{1}}=\frac{\rho_{水}V_{1}}{n_{1}}$,$n_{2}$个小球的总体积$V_{总}=V_{2}-V_{1}$,则一个小球的体积$V_{0}=\frac{V_{总}}{n_{2}}=\frac{V_{2}-V_{1}}{n_{2}}$,所以小球的密度$\rho=\frac{m_{0}}{V_{0}}=\frac{\frac{\rho_{水}V_{1}}{n_{1}}}{\frac{V_{2}-V_{1}}{n_{2}}}=\frac{n_{2}\rho_{水}V_{1}}{n_{1}(V_{2}-V_{1})}$。
查看更多完整答案,请扫码查看


