《2025年亮点给力提优课时作业本八年级物理下册苏科版》

1.（2024·江苏宿迁期中）不同材料组成的$a、b、c$三个实心物体，它们的体积与质量的关系如图所示，下列说法正确的是 （ ）

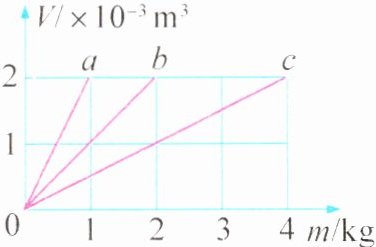
A. 图像越陡，反映物质的密度越大
B. $b$的密度是$c$的两倍
C. 将$b$物体带到太空，其质量变大
D. 当物体$a$与$b$体积相同时，$b$物体质量较大

答案： D

2.（2024·江苏泰州月考）如图所示是某同学研究液体密度时，绘制的甲、乙两种液体的质量$m$与体积$V$的关系图像.由甲图像或乙图像可以得出初步的物理规律是________________________.乙液体的密度为________$kg/m^{3}$.水银的质量与体积关系图像应在________（选填“Ⅰ”“Ⅱ”或“Ⅲ”）区.（水银的密度为$13.6 g/cm^{3}$）

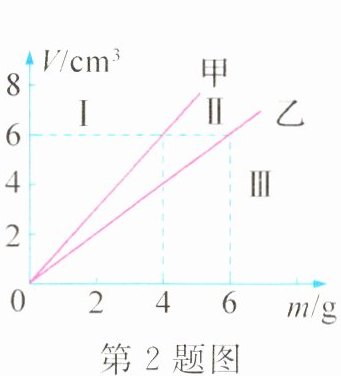
答案： 同种状态下，同种物质的质量与体积成正比
$1×10^{3}$ Ⅲ 解析：由图可知，甲、乙两种液体的质量$m$与体积$V$的关系图像是过原点的直线，则可以得出初步的物理规律是：同种状态下，同种物质的质量与体积成正比. 由图可知，乙液体的密度$\rho_{乙}=\frac{m_{乙}}{V_{乙}}=\frac{6\ g}{6\ cm^{3}} = 1\ g/cm^{3}=1×10^{3}\ kg/m^{3}$；甲液体的密度$\rho_{甲}=\frac{m_{甲}}{V_{甲}}=\frac{4\ g}{6\ cm^{3}}\approx0.67\ g/cm^{3}$，水银的密度为$13.6\ g/cm^{3}$，大于甲、乙两种液体的密度，体积相同时水银的质量最大，由图可知，水银的质量与体积关系图像应在Ⅲ区.

3. 如图所示是用同一个瓶子分别装甲、乙两种液体时，瓶子和液体的总质量随液体体积变化的图像，当用另一个瓶子分别装满甲、乙两种液体时，瓶子和液体的总质量之差为$67.5 g$，则另一个瓶子的容积为________$cm^{3}$.

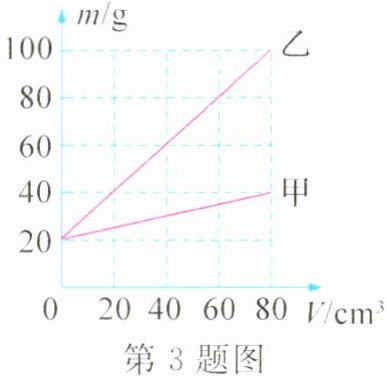
答案： 90 解析：由图像可知，甲液体的体积为$80\ cm^{3}$时的质量$m_{甲}=m_{甲}'-m_{瓶}=40\ g - 20\ g = 20\ g$，则甲的密度$\rho_{甲}=\frac{m_{甲}}{V_{甲}}=\frac{20\ g}{80\ cm^{3}} = 0.25\ g/cm^{3}$，乙液体的体积为$80\ cm^{3}$时的质量$m_{乙}=m_{乙}'-m_{瓶}=100\ g - 20\ g = 80\ g$，则乙的密度$\rho_{乙}=\frac{m_{乙}}{V_{乙}}=\frac{80\ g}{80\ cm^{3}} = 1\ g/cm^{3}$，设另一个瓶子的容积为$V$，由于$\rho_{甲}＜\rho_{乙}$，则有$\rho_{乙}V-\rho_{甲}V = 67.5\ g$，即$1\ g/cm^{3}×V - 0.25\ g/cm^{3}×V = 67.5\ g$，解得$V = 90\ cm^{3}$.

4. 如图甲所示，底面积为$50 cm^{2}$、高为$10 cm$、质量为$100 g$的平底圆柱形容器和一个质量为$100 g$的小球置于水平桌面上（容器厚度忽略不计）.当给容器内盛某种液体时，液体的$m - V$图像如图乙所示；当容器内盛满这种液体后，再将小球轻轻地放入容器中，小球沉入容器底，待液体溢尽擦干容器壁，测得总质量为$560 g$.求：
（1）该液体的密度.
（2）该容器盛满液体时的总质量.
（3）该小球的密度.

答案：
(1)$0.8\ g/cm^{3}$
(2)$500\ g$
(3)$2\ g/cm^{3}$
解析：
(1) 由图乙可知，当液体体积$V_{1}=200\ cm^{3}$时，液体的质量$m_{1}=160\ g$，则液体的密度$\rho=\frac{m_{1}}{V_{1}}=\frac{160\ g}{200\ cm^{3}} = 0.8\ g/cm^{3}$.
(2) 容器内盛满液体时，液体的体积$V_{2}=Sh = 50\ cm^{2}×10\ cm = 500\ cm^{3}$，此时液体的质量$m_{2}=\rho V_{2}=0.8\ g/cm^{3}×500\ cm^{3}=400\ g$，容器的质量$m_{容}=100\ g$，则该容器盛满液体时的总质量$m_{总}=m_{容}+m_{2}=100\ g + 400\ g = 500\ g$.
(3) 将小球轻轻放入容器中，溢出液体的质量$m_{溢}=m_{容}+m_{球}+m_{2}-m_{总}'=100\ g + 100\ g + 400\ g - 560\ g = 40\ g$，小球的体积$V_{球}=V_{溢}=\frac{m_{溢}}{\rho}=\frac{40\ g}{0.8\ g/cm^{3}} = 50\ cm^{3}$，则小球的密度$\rho_{球}=\frac{m_{球}}{V_{球}}=\frac{100\ g}{50\ cm^{3}} = 2\ g/cm^{3}$.