《2025年亮点给力提优课时作业本八年级物理下册苏科版》

4. 如图所示，一个弹簧一端连着一个实心小球(小球密度小于水)，另一端固定在容器底部，放在装满水的装置中处于静止. 若地球的引力减为原来的一半，则下列有关说法不正确的是 （ ）

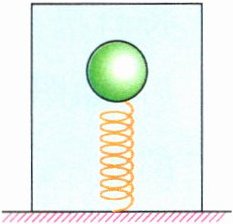
A. 弹簧对小球的弹力变小
B. 小球受到的浮力减为原来一半
C. 若弹簧断了，小球将上浮
D. 若弹簧断了，容器底部受到水的压强不变

答案： D

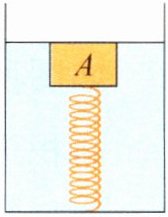
5. 体积为1×10^{-3} m³的物体A与固定在容器底的弹簧相连，现向容器中缓慢注水，直至物体A完全浸没并处于静止状态，如图所示. 此时弹簧对物体A的作用力为2 N. (ρ_{水}=1.0×10³ kg/m³，g取10 N/kg)
(1) 在向容器中注水的过程中，水对容器底部的压强逐渐 ________ (选填“增大”“减小”或“不变”).
(2) 物体A的密度可能为 ________ kg/m³、________ kg/m³.

答案：
(1) 增大
(2) $1.2\times10^{3}$ $0.8\times10^{3}$
解析：
(1) 在向容器中注水的过程中，水的深度增大，由$p = \rho_{水}gh$可知，水对容器底部的压强逐渐增大。
(2) 由图可知，物体$A$浸没在水中，排开水的体积$V_{排}=V_{A}=1\times10^{-3}\ m^{3}$，受到的浮力$F_{浮}=\rho_{水}V_{排}g = 1.0\times10^{3}\ kg/m^{3}\times1\times10^{-3}\ m^{3}\times10\ N/kg = 10\ N$，由题意知，此时弹簧对物体$A$的作用力为$2\ N$，$A$受到重力、浮力及弹力三个力的作用处于静止状态，则三力平衡。有两种可能：① 弹力的方向向上，则$G_{A}=F_{浮}+F_{弹}=10\ N + 2\ N = 12\ N$，此时物体$A$的质量$m_{A}=\frac{G_{A}}{g}=\frac{12\ N}{10\ N/kg}=1.2\ kg$，则物体$A$的密度$\rho_{A}=\frac{m_{A}}{V}=\frac{1.2\ kg}{1\times10^{-3}\ m^{3}}=1.2\times10^{3}\ kg/m^{3}$；② 弹力的方向向下，则$G_{A}=F_{浮}-F_{弹}=10\ N - 2\ N = 8\ N$，此时物体$A$的质量$m_{A}=\frac{G_{A}}{g}=\frac{8\ N}{10\ N/kg}=0.8\ kg$，则物体$A$的密度$\rho_{A}=\frac{m_{A}}{V}=\frac{0.8\ kg}{1\times10^{-3}\ m^{3}}=0.8\times10^{3}\ kg/m^{3}$。

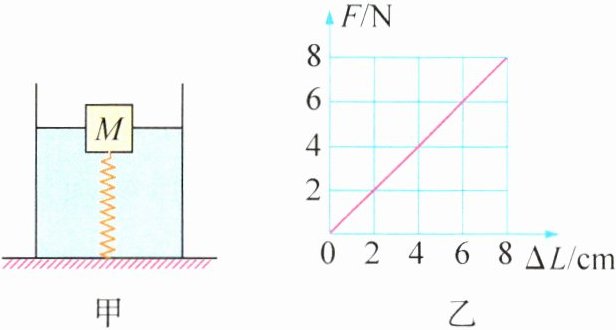
6. (2024·黑龙江绥化模拟)如图甲所示，在水平桌面上有一底面积S = 300 cm²的容器，底部固定一轻质弹簧，弹簧上端连有一棱长为10 cm的正方体物块M，当容器中水的深度为20 cm时，物块M有\frac{2}{5}的体积露出水面，此时弹簧恰好处于原长状态，然后往容器中慢慢加水(水未溢出)，弹簧受到的拉力跟弹簧伸长量的关系如图乙所示，当物块M恰好浸没时，容器对桌面的压力为600 N. (ρ_{水}=1.0×10³ kg/m³，g取10 N/kg)则：
(1) 弹簧恰好处于原长状态时物块M受到的浮力是多少？物块M的密度是多少？
(2) 当物块M恰好浸没时，容器对水平桌面的压强是多少？
(3) 当物块M恰好浸没时，水对容器底部的压强是多少？

答案：
(1) $6\ N$ $0.6\times10^{3}\ kg/m^{3}$
(2) $2\times10^{4}\ Pa$
(3) $2.8\times10^{3}\ Pa$
解析：
(1) 物块$M$的体积$V = L^{3}=(10\ cm)^{3}=1000\ cm^{3}=0.001\ m^{3}$，弹簧恰好处于原长状态时物块$M$受到的浮力$F_{浮}=\rho_{水}V_{排}g=\rho_{水}(1 - \frac{2}{5})Vg = 1.0\times10^{3}\ kg/m^{3}\times\frac{3}{5}\times0.001\ m^{3}\times10\ N/kg = 6\ N$，弹簧处于原长状态时没有发生形变，$M$不受弹力作用，则$G = F_{浮}=6\ N$。物块$M$的密度$\rho_{M}=\frac{m}{V}=\frac{G}{gV}=\frac{6\ N}{10\ N/kg\times0.001\ m^{3}}=0.6\times10^{3}\ kg/m^{3}$。
(2) 当物块$M$恰好浸没时，容器对桌面的压力为$600\ N$，则容器对水平桌面的压强$p_{1}=\frac{F_{压}}{S}=\frac{600\ N}{300\times10^{-4}\ m^{2}}=2\times10^{4}\ Pa$。
(3) 物块$M$恰好浸没在水中时，受到的浮力$F_{浮}'=\rho_{水}V_{排}'g=\rho_{水}Vg = 1.0\times10^{3}\ kg/m^{3}\times0.001\ m^{3}\times10\ N/kg = 10\ N$，则弹簧受到的拉力$F = F_{浮}-G = 10\ N - 6\ N = 4\ N$。由图乙可知，此时弹簧伸长量$\Delta L = 4\ cm$，原来水深$h_{1}=20\ cm$，设物块$M$刚好浸没时水深为$h_{2}$，$M$剩余被浸没的高度$\Delta L_{M}=\frac{2}{5}L=\frac{2}{5}\times10\ cm = 4\ cm$，则$h_{2}=h_{1}+\Delta L+\Delta L_{M}=20\ cm + 4\ cm + 4\ cm = 28\ cm = 0.28\ m$，所以此时水对容器底部的压强$p_{2}=\rho_{水}gh_{2}=1.0\times10^{3}\ kg/m^{3}\times10\ N/kg\times0.28\ m = 2.8\times10^{3}\ Pa$。