第86页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
8. 若样本$x_{1},x_{2},…,x_{n}$的方差为2,则样本$3x_{1}+5,3x_{2}+5,…,3x_{n}+5$的方差是( ).
A.11
B.18
C.23
D.36
A.11
B.18
C.23
D.36
答案:
B
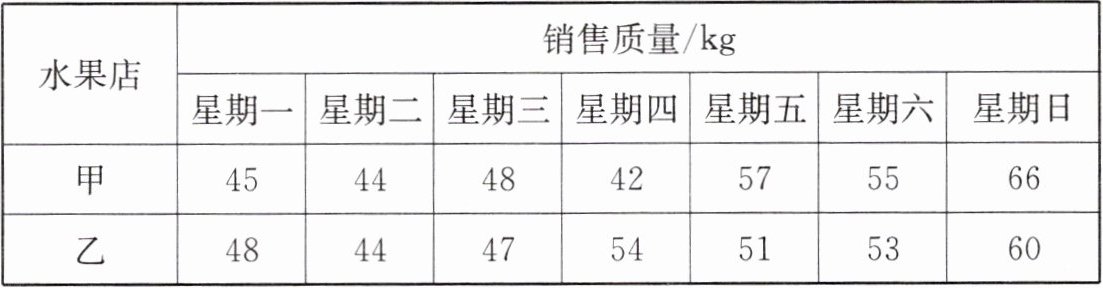
9. 某水果店某周内甲、乙两种水果每天销售情况统计如下表:
| 水果店 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 | 星期六 | 星期日 |
| 甲 | 45 | 44 | 48 | 42 | 57 | 55 | 66 |
| 乙 | 48 | 44 | 47 | 54 | 51 | 53 | 60 |
(1)分别求该周内甲、乙两种水果每天销售量的平均数;
(2)其中,哪一种水果的销售量比较稳定?
| 水果店 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 | 星期六 | 星期日 |
| 甲 | 45 | 44 | 48 | 42 | 57 | 55 | 66 |
| 乙 | 48 | 44 | 47 | 54 | 51 | 53 | 60 |

(1)分别求该周内甲、乙两种水果每天销售量的平均数;
(2)其中,哪一种水果的销售量比较稳定?
答案:
解:
(1) 甲的平均数=(45+44+48+42+57+55+66)÷7=51 (千克)
乙的平均数=(48+44+47+54+51+53+60)÷7=51 (千克),
甲、乙水果平均每天销售51千克.
${S}_{甲}²$=[(45-51)²+(44-51)²+(48-51)²+(42-51)²+(57-51)²+(55-51)²
+(66-51)²]÷7= $\frac{452}{7}$(kg²),
${S}_{乙}²$=[(48-51)²+(44-51)²+(47-51)²+(54-51)²+(51-51)²+(53-51)²
+(60-51)²]÷7= 24(kg²),
因为 ${S}_{甲}²>{S}_{乙}²$
所以乙水果销售量更稳定些.
(1) 甲的平均数=(45+44+48+42+57+55+66)÷7=51 (千克)
乙的平均数=(48+44+47+54+51+53+60)÷7=51 (千克),
甲、乙水果平均每天销售51千克.
${S}_{甲}²$=[(45-51)²+(44-51)²+(48-51)²+(42-51)²+(57-51)²+(55-51)²
+(66-51)²]÷7= $\frac{452}{7}$(kg²),
${S}_{乙}²$=[(48-51)²+(44-51)²+(47-51)²+(54-51)²+(51-51)²+(53-51)²
+(60-51)²]÷7= 24(kg²),
因为 ${S}_{甲}²>{S}_{乙}²$
所以乙水果销售量更稳定些.
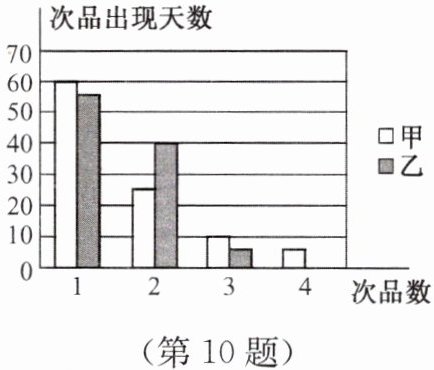
10. 某厂对甲、乙两名优秀工人进行了为期100天的技术考核,结果如图所示:
(1)甲、乙两人每天出现次品个数的众数、中位数、平均数各是多少?
(2)甲生产一天,次品数最有可能是多少个?乙呢?
(3)如果要从这两人中选一个技术较好者为车间组长,你认为谁担任车间组长较合适?
(4)由此例,你能说明众数、中位数与平均数相比有什么不足之处吗?

(1)甲、乙两人每天出现次品个数的众数、中位数、平均数各是多少?
(2)甲生产一天,次品数最有可能是多少个?乙呢?
(3)如果要从这两人中选一个技术较好者为车间组长,你认为谁担任车间组长较合适?
(4)由此例,你能说明众数、中位数与平均数相比有什么不足之处吗?
答案:
解:
(1)观察条形图,可知
甲:众数为1个,中位数为1个;
乙:众数为1个,中位数为1个;
甲的平均数=(60×1+ 25×2+10×3+5×4)÷100=1.6(个) ;
乙的平均数=(55×1+40×2+5×3)÷100=1.5(个)
(2)观察题目所给的统计图,
根据众数的意义,可知甲生产一天,次品数最有可能是1个,乙也是1个;
(3)甲、乙两人每天出现次品的众数、中位数相同,
但乙每天出现次品的平均数较小,一般应确定乙任工长.
(4)计算平均数时,所有的数据都参加运算,它能够较充分地利用数
据所提供的信息,当一组数据中的每个数据与其他数据的差异不
是很大时,通常用平均数表示这组数据的“平均水平”.
在本例中,如果用众数或中位数来考核,就不能较好地反映甲、乙
两人每天出现次品情况的差异.
(1)观察条形图,可知
甲:众数为1个,中位数为1个;
乙:众数为1个,中位数为1个;
甲的平均数=(60×1+ 25×2+10×3+5×4)÷100=1.6(个) ;
乙的平均数=(55×1+40×2+5×3)÷100=1.5(个)
(2)观察题目所给的统计图,
根据众数的意义,可知甲生产一天,次品数最有可能是1个,乙也是1个;
(3)甲、乙两人每天出现次品的众数、中位数相同,
但乙每天出现次品的平均数较小,一般应确定乙任工长.
(4)计算平均数时,所有的数据都参加运算,它能够较充分地利用数
据所提供的信息,当一组数据中的每个数据与其他数据的差异不
是很大时,通常用平均数表示这组数据的“平均水平”.
在本例中,如果用众数或中位数来考核,就不能较好地反映甲、乙
两人每天出现次品情况的差异.
查看更多完整答案,请扫码查看


