《2024年补充习题江苏九年级数学上册苏科版》

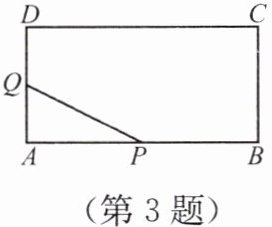
3. 如图,在矩形 $ABCD$ 中,$AB= 24\ cm$,$BC= 12\ cm$,点 $P$ 以 $2\ cm/s$ 的速度从点 $A$ 开始沿边 $AB$ 向点 $B$ 移动,点 $Q$ 以 $1\ cm/s$ 的速度从点 $D$ 开始沿边 $DA$ 向点 $A$ 移动. 如果点 $P$、$Q$ 同时出发,用 $t(s)$ 表示移动的时间 ($0 \leq t \leq 12$),那么当 $t$ 为何值时,$\triangle QAP$ 的面积等于 $32\ cm^2$？

答案： $解:由题意得:AP=2t cm,DQ=t cm,$
$所以AQ=(12-t) cm (0≤t≤12)$
$所以 \frac{1}{2}AQ.AP=\frac{1}{2}(12- t).2t= 32$
$即(12-t)t=32$
$解得t_1=4，t_2= 8$
$答:当t为4s或者8s时, △QAP的面积等于32cm²$

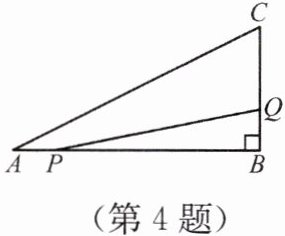
4. 如图,在 $\triangle ABC$ 中,$\angle B= 90^\circ$,$AB= 6\ cm$,$BC= 3\ cm$,点 $P$ 以 $1\ cm/s$ 的速度从点 $A$ 开始沿边 $AB$ 向点 $B$ 移动,点 $Q$ 以 $2\ cm/s$ 的速度从点 $B$ 开始沿边 $BC$ 向点 $C$ 移动. 如果点 $P$、$Q$ 分别从点 $A$、$B$ 同时出发,多少时间后,点 $P$、$Q$ 之间的距离等于 $4\sqrt{2}\ cm$？

答案： $解:设ts后,点P,Q之间的距离为 4\sqrt{2}cm ,$
$则 AP=t cm，BP=(6-t) cm，BQ=2t cm $
$因为BC=3，$
$所以0≤t≤1.5$
$因为∠B=90°$
$所以BP²+BQ²=QP²$
$所以(6- t)²+ (2t)²= (4\sqrt{2})²$
$解得t_1=0.4，t_2= 2(不合题意，舍去)$
$所以t=0.4$
$答:经过0.4s后，P , Q之间的距离是4\sqrt{2}cm$
$ $