《2026年新高考5年真题高中物理全一册通用版湖南专版》

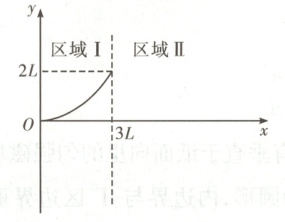
7. [2025·山东卷,12T,4分] (多选) 如图甲所示的 $Oxy$ 平面内，$y$ 轴右侧被直线 $x = 3L$ 分为两个相邻的区域 Ⅰ、Ⅱ。区域 Ⅰ 内充满匀强电场，区域 Ⅱ 内充满垂直 $Oxy$ 平面的匀强磁场，电场和磁场的大小、方向均未知。$t = 0$ 时刻，质量为 $m$、电荷量为 $+q$ 的粒子从 $O$ 点沿 $x$ 轴正向出发，在 $Oxy$ 平面内运动，在区域 Ⅰ 中的运动轨迹是以 $y$ 轴为对称轴的抛物线的一部分，如图甲所示。$t_0$ 时刻粒子第一次到达两区域分界面，在区域 Ⅱ 中运动的 $y-t$ 图像为正弦曲线的一部分，如图乙所示。不计粒子重力。下列说法正确的是


A.区域 Ⅰ 内电场强度大小$E = \frac{4mL}{qt_0^2}$，方向沿 $y$ 轴正方向
B.粒子在区域 Ⅱ 内圆周运动的半径$R = \frac{20L}{3}$
C.区域 Ⅱ 内磁感应强度大小$B = \frac{3m}{5qt_0}$，方向垂直 $Oxy$ 平面向外
D.粒子在区域 Ⅱ 内圆周运动的圆心坐标$(\frac{17L}{3},0)$

答案：
7.参考答案AD
命题意图本题考查带电粒子在电场和磁场中的运动,考查考生的推理能力和分析综合能力。
解题思路由粒子在区域Ⅰ中的运动轨迹是以y轴为对称轴的抛物线的一部分，可以判断出粒子在区域Ⅰ中做类平抛运动，根据运动轨迹可知，粒子受到的电场力方向沿y轴正方向，又粒子带正电，则电场方向沿y轴正方向。设粒子的初速度为$v_{0}，$则沿y轴正方向有$y = \frac{1}{2}at^{2}，$沿x轴正方向有$x = v_{0}t，$由牛顿第二定律有qE = ma，且$t = t_{0}$时，x = 3L，y = 2L，联立解得$v_{0} = \frac{3L}{t_{0}}，$$E = \frac{4mL}{qt_{0}^{2}}。$故A正确。粒子在区域Ⅰ中做类平抛运动进入匀强磁场时的速度大小为$v = \sqrt{v_{0}^{2} + (at_{0})^{2}} = \frac{5L}{t_{0}}。$由粒子在区域Ⅱ中运动的y - t图像为正弦曲线的一部分，可以判断粒子在区域Ⅱ中做匀速圆周运动的运动轨迹如图所示，由左手定则可知，磁场方向垂直Oxy平面向外，由题图乙可知，粒子运动到纵坐标分别为$\frac{10}{3}L$和$ - \frac{10}{3}L$时，粒子沿y轴方向的速度均为0，则粒子在区域Ⅱ内做圆周运动的半径$R = \frac{10}{3}L，$粒子在磁场中运动，根据洛伦兹力提供向心力有$qvB = m\frac{v^{2}}{R}，$联立解得$B = \frac{3m}{2qt_{0}}，$故B、C错误。设粒子进入匀强磁场时的速度方向与竖直方向间的夹角为$\theta，$由速度关系有$sin \theta = \frac{v_{0}}{v} = 0.6，$则由几何关系可得$OO' = 3L + Rcos \theta = \frac{17L}{3}，$即粒子在区域Ⅱ内做圆周运动的圆心坐标为$(\frac{17L}{3},0)，$故D正确。

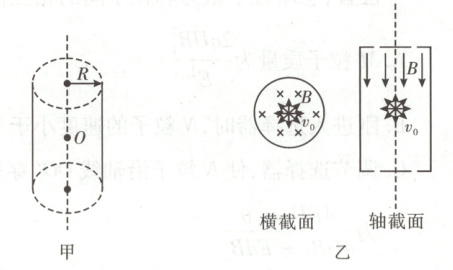
8. [2025·陕西卷,14T,14分] 电子比荷是描述电子性质的重要物理量。在标准理想二极管中利用磁控法可测得比荷，一般其电极结构为圆筒面与中心轴线构成的圆柱体系统，结构简化如图甲所示，足够长圆柱形筒半径为 $R$，正中央有一电子发射源 $O$ 持续向空间各方向发射大量速度大小均为 $v_0$ 的电子。某时刻起筒内加大小可调节且方向沿轴向下的匀强磁场，筒的横截面及轴截面示意图如图乙所示，当磁感应强度大小从 0 缓慢调至 $B_0$ 时，恰好没有电子落到筒壁上，不计电子间相互作用及其重力的影响。求：($R$、$v_0$、$B_0$ 均为已知量)
(1) 电子的比荷$\frac{e}{m}$；
(2) 当磁感应强度大小调至$\frac{1}{2}B_0$时，筒壁上落有电子的区域面积 $S$。

答案： 8.参考答案
(1)$\frac{2v_{0}}{B_{0}R}$
(2)$2\sqrt{3}\pi^{2}R^{2}$
命题意图本题考查电子在匀强磁场中的运动，考查考生的推理能力和应用数学处理物理问题的能力。
解题思路
(1)由题意可知，当磁感应强度大小为B_{0}时，垂直于轴线射出的电子恰好不打到筒壁上，根据几何关系可知，此种情况下电子在磁场中做圆周运动的轨迹半径r = \frac{R}{2}，由洛伦兹力提供向心力有ev_{0}B_{0} = m\frac{v_{0}^{2}}{r}，联立解得电子的比荷$\frac{e}{m} = \frac{2v_{0}}{B_{0}R}$。
(2)当磁感应强度大小调至$\frac{1}{2}B_{0}$时，设发射电子的速度方向与筒的横截面间的夹角为\theta时，电子恰好不打在筒壁上，可将该电子的运动分解为竖直方向上的速度为v_{0}sin \theta的匀速直线运动和横截面内速率为v_{0}cos \theta的圆周运动。则有ev_{0}cos \theta × \frac{1}{2}B_{0} = m\frac{(v_{0}cos \theta)^{2}}{r}，联立解得\theta = 60^{\circ}，即发射电子的速度方向与筒的横截面成60^{\circ}角时，电子恰好不打在筒壁上。对该情况下的电子，根据圆周运动知识可知电子做圆周运动的周期T = \frac{2\pi r}{v_{0}cos 60^{\circ}} = \frac{2\pi R}{v_{0}}。电子运动半个周期时恰好运动至轨迹与筒壁切点处，电子在竖直方向上做匀速直线运动，则有h = v_{0}sin 60^{\circ} × \frac{T}{2} = \frac{\sqrt{3}}{2}\pi R，由几何关系可得筒壁上落有电子的区域面积S = 2\pi R × 2h = 2\sqrt{3}\pi^{2}R^{2}。