2026年新高考5年真题高中物理全一册通用版湖南专版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2026年新高考5年真题高中物理全一册通用版湖南专版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第11页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
8. 某电磁缓冲装置如图所示,两足够长的平行金属导轨置于同一水平面内,导轨左端与一阻值为 $R$ 的定值电阻相连,导轨 $BC$ 段与 $B_1C_1$ 段粗糙,其余部分光滑,$AA_1$ 右侧处于竖直向下的匀强磁场中,一质量为 $m$ 的金属杆垂直导轨放置。现让金属杆以初速度 $v_0$ 沿导轨向右经过 $AA_1$ 进入磁场,最终恰好停在 $CC_1$ 处。已知金属杆接入导轨之间的阻值为 $R$,与粗糙导轨间的动摩擦因数为 $\mu$,$AB = BC = d$。导轨电阻不计,重力加速度为 $g$,下列说法正确的是 (
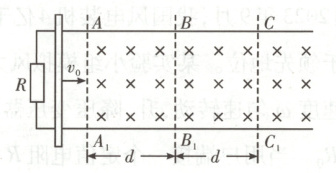
A.金属杆经过 $BB_1$ 的速度为 $\frac{v_0}{2}$
B.在整个过程中,定值电阻 $R$ 产生的热量为 $\frac{1}{2}mv_0^2 - \frac{1}{2}\mu mgd$
C.金属杆经过 $AA_1B_1B$ 与 $BB_1C_1C$ 区域,金属杆所受安培力的冲量相同
D.若将金属杆的初速度加倍,则金属杆在磁场中运动的距离大于原来的 2 倍
CD
)
A.金属杆经过 $BB_1$ 的速度为 $\frac{v_0}{2}$
B.在整个过程中,定值电阻 $R$ 产生的热量为 $\frac{1}{2}mv_0^2 - \frac{1}{2}\mu mgd$
C.金属杆经过 $AA_1B_1B$ 与 $BB_1C_1C$ 区域,金属杆所受安培力的冲量相同
D.若将金属杆的初速度加倍,则金属杆在磁场中运动的距离大于原来的 2 倍
答案:
8.参考答案CD
命题意图本题考查法拉第电磁感应定律、动量定理和能量守恒定律,考查考生的推理能力和分析综合能力。
解题思路设金属杆经过$BB_{1}$的速度大小为$v_{1}$,则金属杆从$AA_{1}$运动到$BB_{1}$的过程,由动量定理有$-\frac{B^{2}L^{2}\overline{v_{1}}}{2R}t_{1}=m(v_{0}-v_{1})$,又$v_{1}t_{1}=d$,则有$\frac{B^{2}L^{2}d}{2R}=m(v_{0}-v_{1})$;金属杆从$BB_{1}$运动到$CC_{1}$的过程,由动量定理有$-\frac{B^{2}L^{2}\overline{v_{2}}}{2R}t_{2}+\mu mg t_{2}=mv_{1}-mv_{2}$,又$v_{2}t_{2}=d$,则有$\frac{B^{2}L^{2}d}{2R}+\mu mg t_{2}=mv_{1}-mv_{2}$,分析可知$v_{0}-v_{1}<v_{1}-v_{2}$,解得$v_{1}>\frac{v_{0}}{2}$,即金属杆经过$BB_{1}$的速度大于$\frac{v_{0}}{2}$,A错误。整个过程,由能量守恒定律可得$\frac{1}{2}mv_{0}^{2}=Q_{R}+Q_{杆}+\mu mgd$,又通过定值电阻$R$和金属杆的电流时刻相等,则由焦耳定律可知$Q_{R}=Q_{杆}$,联立可得$Q_{R}=\frac{1}{4}mv_{0}^{2}-\frac{1}{2}\mu mgd$,B错误。规定水平向左为正方向,结合A项分析可知,金属杆经过$AA_{1}B_{1}B$区域,金属杆所受安培力的冲量$I_{1}=\frac{B^{2}L^{2}d}{2R}$,金属杆经过$BB_{1}C_{1}C$区域,金属杆所受安培力的冲量$I_{2}=\frac{B^{2}L^{2}d}{2R}$,可得$I_{1}=I_{2}$,即金属杆经过$AA_{1}B_{1}B$与$BB_{1}C_{1}C$区域,金属杆所受安培力的冲量相同,C正确。若将金属杆的初速度加倍,则金属杆从$AA_{1}$运动到$BB_{1}$的过程,由动量定理有$\frac{B^{2}L^{2}\overline{v_{3}}}{2R}t_{3}=\frac{B^{2}L^{2}d}{2R}=m(2v_{0}-v_{B})$,金属杆从$BB_{1}$运动到$CC_{1}$的过程,由动量定理有$\frac{B^{2}L^{2}\overline{v_{4}}}{2R}t_{4}+\mu mg t_{4}=m(v_{B}-v_{C})$,即$\frac{B^{2}L^{2}d}{2R}+\mu mg t_{4}=m(v_{B}-v_{C})$,又由运动学知识可知$t_{4}<t_{2}$,结合A项分析可得金属杆经过$CC_{1}$的速度$v_{C}>v_{0}$,金属杆经过$CC_{1}$之后的运动过程,由动量定理有$-\frac{B^{2}L^{2}}{2R}t_{5}=\frac{B^{2}L^{2}\Delta x}{2R}=mv_{C}>mv_{0}$,又由A项分析有$\frac{B^{2}L^{2}d}{2R}<m×\frac{1}{2}v_{0}$,可得$\Delta x>2d$,则金属杆在磁场中运动的距离为$x =2d+\Delta x>4d$,即金属杆在磁场中运动的距离大于原来的$2$倍,D正确。
命题意图本题考查法拉第电磁感应定律、动量定理和能量守恒定律,考查考生的推理能力和分析综合能力。
解题思路设金属杆经过$BB_{1}$的速度大小为$v_{1}$,则金属杆从$AA_{1}$运动到$BB_{1}$的过程,由动量定理有$-\frac{B^{2}L^{2}\overline{v_{1}}}{2R}t_{1}=m(v_{0}-v_{1})$,又$v_{1}t_{1}=d$,则有$\frac{B^{2}L^{2}d}{2R}=m(v_{0}-v_{1})$;金属杆从$BB_{1}$运动到$CC_{1}$的过程,由动量定理有$-\frac{B^{2}L^{2}\overline{v_{2}}}{2R}t_{2}+\mu mg t_{2}=mv_{1}-mv_{2}$,又$v_{2}t_{2}=d$,则有$\frac{B^{2}L^{2}d}{2R}+\mu mg t_{2}=mv_{1}-mv_{2}$,分析可知$v_{0}-v_{1}<v_{1}-v_{2}$,解得$v_{1}>\frac{v_{0}}{2}$,即金属杆经过$BB_{1}$的速度大于$\frac{v_{0}}{2}$,A错误。整个过程,由能量守恒定律可得$\frac{1}{2}mv_{0}^{2}=Q_{R}+Q_{杆}+\mu mgd$,又通过定值电阻$R$和金属杆的电流时刻相等,则由焦耳定律可知$Q_{R}=Q_{杆}$,联立可得$Q_{R}=\frac{1}{4}mv_{0}^{2}-\frac{1}{2}\mu mgd$,B错误。规定水平向左为正方向,结合A项分析可知,金属杆经过$AA_{1}B_{1}B$区域,金属杆所受安培力的冲量$I_{1}=\frac{B^{2}L^{2}d}{2R}$,金属杆经过$BB_{1}C_{1}C$区域,金属杆所受安培力的冲量$I_{2}=\frac{B^{2}L^{2}d}{2R}$,可得$I_{1}=I_{2}$,即金属杆经过$AA_{1}B_{1}B$与$BB_{1}C_{1}C$区域,金属杆所受安培力的冲量相同,C正确。若将金属杆的初速度加倍,则金属杆从$AA_{1}$运动到$BB_{1}$的过程,由动量定理有$\frac{B^{2}L^{2}\overline{v_{3}}}{2R}t_{3}=\frac{B^{2}L^{2}d}{2R}=m(2v_{0}-v_{B})$,金属杆从$BB_{1}$运动到$CC_{1}$的过程,由动量定理有$\frac{B^{2}L^{2}\overline{v_{4}}}{2R}t_{4}+\mu mg t_{4}=m(v_{B}-v_{C})$,即$\frac{B^{2}L^{2}d}{2R}+\mu mg t_{4}=m(v_{B}-v_{C})$,又由运动学知识可知$t_{4}<t_{2}$,结合A项分析可得金属杆经过$CC_{1}$的速度$v_{C}>v_{0}$,金属杆经过$CC_{1}$之后的运动过程,由动量定理有$-\frac{B^{2}L^{2}}{2R}t_{5}=\frac{B^{2}L^{2}\Delta x}{2R}=mv_{C}>mv_{0}$,又由A项分析有$\frac{B^{2}L^{2}d}{2R}<m×\frac{1}{2}v_{0}$,可得$\Delta x>2d$,则金属杆在磁场中运动的距离为$x =2d+\Delta x>4d$,即金属杆在磁场中运动的距离大于原来的$2$倍,D正确。
9. 1834 年,洛埃利用平面镜得到杨氏双缝干涉的结果(称洛埃镜实验),平面镜沿 $OA$ 放置,靠近并垂直于光屏。某同学重复此实验时,平面镜意外倾斜了某微小角度 $\theta$,如图所示。$S$ 为单色点光源。下列说法正确的是 (

A.沿 $AO$ 向左略微平移平面镜,干涉条纹不移动
B.沿 $OA$ 向右略微平移平面镜,干涉条纹间距减小
C.若 $\theta = 0°$,沿 $OA$ 向右略微平移平面镜,干涉条纹间距不变
D.若 $\theta = 0°$,沿 $AO$ 向左略微平移平面镜,干涉条纹向 $A$ 处移动
BC
)
A.沿 $AO$ 向左略微平移平面镜,干涉条纹不移动
B.沿 $OA$ 向右略微平移平面镜,干涉条纹间距减小
C.若 $\theta = 0°$,沿 $OA$ 向右略微平移平面镜,干涉条纹间距不变
D.若 $\theta = 0°$,沿 $AO$ 向左略微平移平面镜,干涉条纹向 $A$ 处移动
答案:
9.参考答案BC
命题意图本题考查光的双缝干涉,考查考生的理解能力和推理能力。
解题思路当$\theta\neq0^{\circ}$,且$\theta$非常小时,作出$S$关于平面镜对称的点$S'$,如图甲所示,则$S$和$S'$相当于双缝干涉实验中的双缝,若沿$AO$向左略微平移平面镜,则双缝间距减小,双缝到屏的距离增大,结合双缝干涉条纹间距公式$\Delta x=\frac{l}{d}\lambda$可知干涉条纹间距增大,干涉条纹移动。若沿$OA$向右略微平移平面镜,则双缝间距增大,双缝到屏的距离减小,结合双缝干涉条纹间距公式$\Delta x=\frac{l}{d}\lambda$可知干涉条纹间距减小。若$\theta =0^{\circ}$,作出$S$关于平面镜对称的点$S''$,如图乙所示,可知无论是沿$OA$向右略微平移平面镜,还是沿$AO$向左略微平移平面镜,$S$和$S''$的位置均不变,则干涉条纹不移动,干涉条纹间距不变。故B、C正确,A、D错误。


9.参考答案BC
命题意图本题考查光的双缝干涉,考查考生的理解能力和推理能力。
解题思路当$\theta\neq0^{\circ}$,且$\theta$非常小时,作出$S$关于平面镜对称的点$S'$,如图甲所示,则$S$和$S'$相当于双缝干涉实验中的双缝,若沿$AO$向左略微平移平面镜,则双缝间距减小,双缝到屏的距离增大,结合双缝干涉条纹间距公式$\Delta x=\frac{l}{d}\lambda$可知干涉条纹间距增大,干涉条纹移动。若沿$OA$向右略微平移平面镜,则双缝间距增大,双缝到屏的距离减小,结合双缝干涉条纹间距公式$\Delta x=\frac{l}{d}\lambda$可知干涉条纹间距减小。若$\theta =0^{\circ}$,作出$S$关于平面镜对称的点$S''$,如图乙所示,可知无论是沿$OA$向右略微平移平面镜,还是沿$AO$向左略微平移平面镜,$S$和$S''$的位置均不变,则干涉条纹不移动,干涉条纹间距不变。故B、C正确,A、D错误。


10. 如图,光滑水平面内建立直角坐标系 $xOy$,A、B 两小球同时从 $O$ 点出发,A 球速度大小为 $v_1$、方向沿 $x$ 轴正方向,B 球速度大小为 $v_2 = 2$ m/s、方向与 $x$ 轴正方向夹角为 $\theta$。坐标系第一象限中有一个挡板 $L$,与 $x$ 轴夹角为 $\alpha$。B 球与挡板 $L$ 发生碰撞,碰后 B 球速度大小变为 1 m/s,碰撞前后 B 球的速度方向与挡板 $L$ 法线的夹角相同,且分别位于法线两侧。不计碰撞时间和空气阻力,若 A、B 两小球能相遇,下列说法正确的是 (
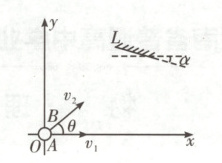
A.若 $\theta = 15°$,则 $v_1$ 的最大值为 $\sqrt{2}$ m/s,且 $\alpha = 15°$
B.若 $\theta = 15°$,则 $v_1$ 的最大值为 $\frac{2}{3}\sqrt{3}$ m/s,且 $\alpha = 0°$
C.若 $\theta = 30°$,则 $v_1$ 的最大值为 $\frac{2}{3}\sqrt{3}$ m/s,且 $\alpha = 0°$
D.若 $\theta = 30°$,则 $v_1$ 的最大值为 $\sqrt{2}$ m/s,且 $\alpha = 15°$
AC
)
A.若 $\theta = 15°$,则 $v_1$ 的最大值为 $\sqrt{2}$ m/s,且 $\alpha = 15°$
B.若 $\theta = 15°$,则 $v_1$ 的最大值为 $\frac{2}{3}\sqrt{3}$ m/s,且 $\alpha = 0°$
C.若 $\theta = 30°$,则 $v_1$ 的最大值为 $\frac{2}{3}\sqrt{3}$ m/s,且 $\alpha = 0°$
D.若 $\theta = 30°$,则 $v_1$ 的最大值为 $\sqrt{2}$ m/s,且 $\alpha = 15°$
答案:
10.参考答案AC
命题意图本题考查特殊的追击相遇问题,考查考生的推理能力和应用数学处理物理问题的能力。
解题思路作出两小球的运动路径,如图所示。小球$B$与挡板$L$碰撞后的速度与碰撞前的速度之比$\frac{v_{2}'}{v_{2}}=\frac{1}{2}=\sin30^{\circ}$。设小球$B$与挡板$L$的碰撞点为$D$,小球$A、B$的相遇点为$C$,根据几何关系可知$\angle DCO =2\alpha+\theta$。作辅助线$OE$使$\angle DOE =30^{\circ}$,过$D$点作$OE$的垂线交$OE$于点$E$,则$DE=\frac{1}{2}OD$。可将$B$球的运动等效为从$E$点沿$E\rightarrow D\rightarrow C$以$v_{2}'=1m/s$的速度运动到$C$点,则$v_{1}=\frac{OC}{t}=\frac{OC}{CD + DE}v_{2}'$,过$C$点作$OE$的垂线交$OE$于点$F$,则$CD + DE\geqslant CF$,可得$v_{1}\leqslant\frac{OC}{CF}v_{2}'=\frac{1}{\sin(\theta + 30^{\circ})}m/s$。当$\theta =15^{\circ}$时,$v_{1max}=\frac{1}{\sin45^{\circ}}m/s=\sqrt{2}m/s$,此时$2\alpha+\theta =90^{\circ}-45^{\circ}$,解得$\alpha =15^{\circ}$;当$\theta =30^{\circ}$时,$v_{1max}=\frac{1}{\sin60^{\circ}}m/s=\frac{2\sqrt{3}}{3}m/s$,此时$2\alpha+\theta =90^{\circ}-60^{\circ}$,解得$\alpha =0^{\circ}$。故A、C正确,B、D错误。

10.参考答案AC
命题意图本题考查特殊的追击相遇问题,考查考生的推理能力和应用数学处理物理问题的能力。
解题思路作出两小球的运动路径,如图所示。小球$B$与挡板$L$碰撞后的速度与碰撞前的速度之比$\frac{v_{2}'}{v_{2}}=\frac{1}{2}=\sin30^{\circ}$。设小球$B$与挡板$L$的碰撞点为$D$,小球$A、B$的相遇点为$C$,根据几何关系可知$\angle DCO =2\alpha+\theta$。作辅助线$OE$使$\angle DOE =30^{\circ}$,过$D$点作$OE$的垂线交$OE$于点$E$,则$DE=\frac{1}{2}OD$。可将$B$球的运动等效为从$E$点沿$E\rightarrow D\rightarrow C$以$v_{2}'=1m/s$的速度运动到$C$点,则$v_{1}=\frac{OC}{t}=\frac{OC}{CD + DE}v_{2}'$,过$C$点作$OE$的垂线交$OE$于点$F$,则$CD + DE\geqslant CF$,可得$v_{1}\leqslant\frac{OC}{CF}v_{2}'=\frac{1}{\sin(\theta + 30^{\circ})}m/s$。当$\theta =15^{\circ}$时,$v_{1max}=\frac{1}{\sin45^{\circ}}m/s=\sqrt{2}m/s$,此时$2\alpha+\theta =90^{\circ}-45^{\circ}$,解得$\alpha =15^{\circ}$;当$\theta =30^{\circ}$时,$v_{1max}=\frac{1}{\sin60^{\circ}}m/s=\frac{2\sqrt{3}}{3}m/s$,此时$2\alpha+\theta =90^{\circ}-60^{\circ}$,解得$\alpha =0^{\circ}$。故A、C正确,B、D错误。

查看更多完整答案,请扫码查看


