2026年新高考5年真题高中物理全一册通用版湖南专版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2026年新高考5年真题高中物理全一册通用版湖南专版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第31页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
16. [物理—— 选修 3 - 4](13 分)
(1) (5 分) 下端附着重物的粗细均匀木棒,竖直浮在河面,在重力和浮力作用下,沿竖直方向做频率为 $1\ Hz$ 的简谐运动;与此同时,木棒在水平方向上随河水做匀速直线运动,如图(a)所示。以木棒所受浮力$F$为纵轴,木棒水平位移$x$为横轴建立直角坐标系,浮力$F$随水平位移$x$的变化如图(b)所示。已知河水密度为$\rho$,木棒横截面积为$S$,重力加速度大小为$g$。下列说法正确的是

A. $x$ 从 $0.05\ m$ 到 $0.15\ m$ 的过程中,木棒的动能先增大后减小
B. $x$ 从 $0.21\ m$ 到 $0.25\ m$ 的过程中,木棒加速度方向竖直向下,大小逐渐变小
C. $x=0.35\ m$ 和 $x=0.45\ m$ 时,木棒的速度大小相等,方向相反
D. 木棒在竖直方向做简谐运动的振幅为 $\frac{F_1-F_2}{2\rho Sg}$
E. 木棒的运动为向$x$轴正方向传播的机械横波,波速为 $0.4\ m/s$
(2) (8 分) 如图,某种防窥屏由透明介质和对光完全吸收的屏障构成,其中屏障垂直于屏幕平行排列,可实现对像素单元可视角度$\theta$的控制(可视角度$\theta$定义为某像素单元发出的光在图示平面内折射到空气后最大折射角的 2 倍)。透明介质的折射率 $n=2$,屏障间隙 $L=0.8\ mm$。发光像素单元紧贴屏下,位于相邻两屏障的正中间。不考虑光的衍射。
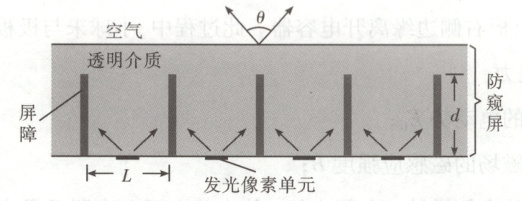
(ⅰ) 若把发光像素单元视为点光源,要求可视角度$\theta$控制为 $60°$,求屏障的高度$d$;
(ⅱ) 若屏障高度 $d=1.0\ mm$,且发光像素单元的宽度不能忽略,求像素单元宽度$x$最小为多少时,其可视角度$\theta$刚好被扩为 $180°$(只要看到像素单元的任意一点,即视为能看到该像素单元)。
(1) (5 分) 下端附着重物的粗细均匀木棒,竖直浮在河面,在重力和浮力作用下,沿竖直方向做频率为 $1\ Hz$ 的简谐运动;与此同时,木棒在水平方向上随河水做匀速直线运动,如图(a)所示。以木棒所受浮力$F$为纵轴,木棒水平位移$x$为横轴建立直角坐标系,浮力$F$随水平位移$x$的变化如图(b)所示。已知河水密度为$\rho$,木棒横截面积为$S$,重力加速度大小为$g$。下列说法正确的是
ABD
(选对 1 个得 2 分,选对 2 个得 4 分,选对 3 个得 5 分。每选错 1 个扣 3 分,最低得分为 0 分)。
A. $x$ 从 $0.05\ m$ 到 $0.15\ m$ 的过程中,木棒的动能先增大后减小
B. $x$ 从 $0.21\ m$ 到 $0.25\ m$ 的过程中,木棒加速度方向竖直向下,大小逐渐变小
C. $x=0.35\ m$ 和 $x=0.45\ m$ 时,木棒的速度大小相等,方向相反
D. 木棒在竖直方向做简谐运动的振幅为 $\frac{F_1-F_2}{2\rho Sg}$
E. 木棒的运动为向$x$轴正方向传播的机械横波,波速为 $0.4\ m/s$
(2) (8 分) 如图,某种防窥屏由透明介质和对光完全吸收的屏障构成,其中屏障垂直于屏幕平行排列,可实现对像素单元可视角度$\theta$的控制(可视角度$\theta$定义为某像素单元发出的光在图示平面内折射到空气后最大折射角的 2 倍)。透明介质的折射率 $n=2$,屏障间隙 $L=0.8\ mm$。发光像素单元紧贴屏下,位于相邻两屏障的正中间。不考虑光的衍射。

(ⅰ) 若把发光像素单元视为点光源,要求可视角度$\theta$控制为 $60°$,求屏障的高度$d$;
(ⅱ) 若屏障高度 $d=1.0\ mm$,且发光像素单元的宽度不能忽略,求像素单元宽度$x$最小为多少时,其可视角度$\theta$刚好被扩为 $180°$(只要看到像素单元的任意一点,即视为能看到该像素单元)。
答案:
16.参考答案
(1)ABD
(2)(i)$\frac{2\sqrt{15}}{5}$mm (ii)$\frac{10\sqrt{3}-12}{15}$mm
命题意图本题考查简谐运动、光的折射和全反射,考查考生的推理能力和应用数学处理物理问题的能力。
解题思路
(1)由简谐运动的对称性可知,木棒的水平位移为0.1m、0.3m或0.5m时,木棒处于平衡位置,则x从0.05m到0.15m的过程中,木棒在竖直方向从平衡位置下方向上经平衡位置后到达平衡位置上方,木棒的速度先增大后减小,所以木棒的动能先增大后减小,A正确。x从0.21m到0.25m的过程中,木棒始终处于平衡位置上方,由题图(b)可知木棒受到的浮力增大,根据Mg - F_{浮}=Ma可知,木棒的加速度方向竖直向下,大小逐渐减小,B正确。x = 0.35m和x = 0.45m时,由题图(b)可知木棒所受浮力大小相等,说明木棒位于同一位置,且在竖直方向的分速度大小相等、方向相反,又木棒在水平方向的分速度始终相同,所以在x = 0.35m和x = 0.45m时,木棒的速度大小相等,方向不相反,C错误。木棒在竖直方向的简谐运动可类比为竖直方向的弹簧振子,设木棒重心下的长度为L,回复力系数为k,木棒位于平衡位置时重心在水面下方Δx_{0}处,则有ρSg(L+Δx_{0}) = Mg,木棒重心在平衡位置上方最大位移A处时,则有Mg - F_{2}=Mg - ρSg(L+Δx_{0}-A)=kA,木棒重心在平衡位置下方最大位移A处时,则有F_{1}-Mg = ρSg(L+Δx_{0}+A)-Mg = kA,联立解得k = ρSg,A = $\frac{F_{1}-F_{2}}{2ρSg}$,D正确。木棒在水平方向上随河水做匀速直线运动,而机械横波的质点并不随波迁移,则木棒的运动不能看成向x轴正方向传播的机械横波,木棒在水平方向运动的速度为v = $\frac{0.5 - 0.1}{1}$m/s = 0.4m/s,E错误。
(2)(i)发光像素单元射到屏障上的光被完全吸收,考虑射到屏障顶端的光射到透明介质和空气界面,折射后从界面射向空气,由题意可知θ = 60°,则折射角r = $\frac{\theta}{2}$ = 30°,设光在透明介质中的入射角为i,则$\frac{sinr}{sini}$ = n,解得sini = $\frac{1}{4}$。由几何关系可知sini = $\frac{\frac{L}{2}}{\sqrt{d^{2}+(\frac{L}{2})^{2}}}$,联立解得d = $\frac{2\sqrt{15}}{5}$mm。
(ii)若可视角度θ刚好被扩为180°,则$\frac{180°}{2}$ = 90°,即此时光线在界面处发生全反射,可得光线在界面处的入射角的正弦值sinC = $\frac{1}{n}$ = $\frac{1}{2}$,解得C = 30°。则发光像素单元发光点距离屏障的距离为x_{1}=dtanC = $\frac{\sqrt{3}}{3}$mm,由几何关系可知像素单元宽度x的最小值为x_{min}=2(x_{1}-$\frac{L}{2}$) = $\frac{10\sqrt{3}-12}{15}$mm
(1)ABD
(2)(i)$\frac{2\sqrt{15}}{5}$mm (ii)$\frac{10\sqrt{3}-12}{15}$mm
命题意图本题考查简谐运动、光的折射和全反射,考查考生的推理能力和应用数学处理物理问题的能力。
解题思路
(1)由简谐运动的对称性可知,木棒的水平位移为0.1m、0.3m或0.5m时,木棒处于平衡位置,则x从0.05m到0.15m的过程中,木棒在竖直方向从平衡位置下方向上经平衡位置后到达平衡位置上方,木棒的速度先增大后减小,所以木棒的动能先增大后减小,A正确。x从0.21m到0.25m的过程中,木棒始终处于平衡位置上方,由题图(b)可知木棒受到的浮力增大,根据Mg - F_{浮}=Ma可知,木棒的加速度方向竖直向下,大小逐渐减小,B正确。x = 0.35m和x = 0.45m时,由题图(b)可知木棒所受浮力大小相等,说明木棒位于同一位置,且在竖直方向的分速度大小相等、方向相反,又木棒在水平方向的分速度始终相同,所以在x = 0.35m和x = 0.45m时,木棒的速度大小相等,方向不相反,C错误。木棒在竖直方向的简谐运动可类比为竖直方向的弹簧振子,设木棒重心下的长度为L,回复力系数为k,木棒位于平衡位置时重心在水面下方Δx_{0}处,则有ρSg(L+Δx_{0}) = Mg,木棒重心在平衡位置上方最大位移A处时,则有Mg - F_{2}=Mg - ρSg(L+Δx_{0}-A)=kA,木棒重心在平衡位置下方最大位移A处时,则有F_{1}-Mg = ρSg(L+Δx_{0}+A)-Mg = kA,联立解得k = ρSg,A = $\frac{F_{1}-F_{2}}{2ρSg}$,D正确。木棒在水平方向上随河水做匀速直线运动,而机械横波的质点并不随波迁移,则木棒的运动不能看成向x轴正方向传播的机械横波,木棒在水平方向运动的速度为v = $\frac{0.5 - 0.1}{1}$m/s = 0.4m/s,E错误。
(2)(i)发光像素单元射到屏障上的光被完全吸收,考虑射到屏障顶端的光射到透明介质和空气界面,折射后从界面射向空气,由题意可知θ = 60°,则折射角r = $\frac{\theta}{2}$ = 30°,设光在透明介质中的入射角为i,则$\frac{sinr}{sini}$ = n,解得sini = $\frac{1}{4}$。由几何关系可知sini = $\frac{\frac{L}{2}}{\sqrt{d^{2}+(\frac{L}{2})^{2}}}$,联立解得d = $\frac{2\sqrt{15}}{5}$mm。
(ii)若可视角度θ刚好被扩为180°,则$\frac{180°}{2}$ = 90°,即此时光线在界面处发生全反射,可得光线在界面处的入射角的正弦值sinC = $\frac{1}{n}$ = $\frac{1}{2}$,解得C = 30°。则发光像素单元发光点距离屏障的距离为x_{1}=dtanC = $\frac{\sqrt{3}}{3}$mm,由几何关系可知像素单元宽度x的最小值为x_{min}=2(x_{1}-$\frac{L}{2}$) = $\frac{10\sqrt{3}-12}{15}$mm
查看更多完整答案,请扫码查看


