2026年学易优高考二轮总复习数学
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2026年学易优高考二轮总复习数学 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第85页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
【样题 2】(2025·郑州质检节选)已知椭圆 $ C:\frac{x^{2}}{2}+y^{2}=1 $ 的上顶点为 $ A $,过点 $ (0,\frac{1}{2}) $ 的直线 $ l $ 与椭圆 $ C $ 交于两个不同的点 $ P,Q $,直线 $ AP $ 与 $ x $ 轴交于点 $ M $,直线 $ AQ $ 与 $ x $ 轴交于点 $ N $。证明:以 $ MN $ 为直径的圆过 $ y $ 轴上的定点。
答案:
证明:由题意知直线l的斜率存在,可设直线$l:y = kx+\frac{1}{2}$,$P(x_1,y_1)$,$Q(x_2,y_2)$。
由$\begin{cases}y = kx+\frac{1}{2}\frac{x^{2}}{2}+y^{2}=1\end{cases}$得$(4k^{2}+2)x^{2}+4kx - 3 = 0$。
所以$x_1 + x_2=-\frac{4k}{4k^{2}+2}$,$x_1x_2=-\frac{3}{4k^{2}+2}$。
直线AP的方程为$y=\frac{y_1 - 1}{x_1}x + 1$,直线AQ的方程为$y=\frac{y_2 - 1}{x_2}x + 1$。
可得$M(\frac{-x_1}{y_1 - 1},0)$,$N(\frac{-x_2}{y_2 - 1},0)$。
以MN为直径的圆的方程为$(x+\frac{x_1}{y_1 - 1})(x+\frac{x_2}{y_2 - 1})+y^{2}=0$,即$x^{2}+y^{2}+(\frac{x_1}{y_1 - 1}+\frac{x_2}{y_2 - 1})x+\frac{x_1x_2}{(y_1 - 1)(y_2 - 1)}=0$ ①。
因为$\frac{x_1x_2}{(y_1 - 1)(y_2 - 1)}=\frac{x_1x_2}{(kx_1-\frac{1}{2})(kx_2-\frac{1}{2})}=\frac{4x_1x_2}{4k^{2}x_1x_2-2k(x_1 + x_2)+1}=\frac{-12}{-12k^{2}+8k^{2}+4k^{2}+2}=-6$。
所以在①中,令$x = 0$,得$y^{2}=6$,即以MN为直径的圆过$y$轴上的定点$(0,\pm\sqrt{6})$。
由$\begin{cases}y = kx+\frac{1}{2}\frac{x^{2}}{2}+y^{2}=1\end{cases}$得$(4k^{2}+2)x^{2}+4kx - 3 = 0$。
所以$x_1 + x_2=-\frac{4k}{4k^{2}+2}$,$x_1x_2=-\frac{3}{4k^{2}+2}$。
直线AP的方程为$y=\frac{y_1 - 1}{x_1}x + 1$,直线AQ的方程为$y=\frac{y_2 - 1}{x_2}x + 1$。
可得$M(\frac{-x_1}{y_1 - 1},0)$,$N(\frac{-x_2}{y_2 - 1},0)$。
以MN为直径的圆的方程为$(x+\frac{x_1}{y_1 - 1})(x+\frac{x_2}{y_2 - 1})+y^{2}=0$,即$x^{2}+y^{2}+(\frac{x_1}{y_1 - 1}+\frac{x_2}{y_2 - 1})x+\frac{x_1x_2}{(y_1 - 1)(y_2 - 1)}=0$ ①。
因为$\frac{x_1x_2}{(y_1 - 1)(y_2 - 1)}=\frac{x_1x_2}{(kx_1-\frac{1}{2})(kx_2-\frac{1}{2})}=\frac{4x_1x_2}{4k^{2}x_1x_2-2k(x_1 + x_2)+1}=\frac{-12}{-12k^{2}+8k^{2}+4k^{2}+2}=-6$。
所以在①中,令$x = 0$,得$y^{2}=6$,即以MN为直径的圆过$y$轴上的定点$(0,\pm\sqrt{6})$。
训练 1(2025·荆州适应性考试)已知 $ F_{1}(-2,0),F_{2}(2,0) $,$ M $ 是圆 $ O:x^{2}+y^{2}=1 $ 上任意一点,$ F_{1} $ 关于点 $ M $ 的对称点为 $ N $,线段 $ F_{1}N $ 的垂直平分线与直线 $ F_{2}N $ 相交于点 $ T $,记点 $ T $ 的轨迹为曲线 $ C $。
(1) 求曲线 $ C $ 的方程;
(2) 设 $ E(t,t)(t>0) $ 为曲线 $ C $ 上一点,不与 $ x $ 轴垂直的直线 $ l $ 与曲线 $ C $ 交于 $ G,H $ 两点(异于 $ E $ 点)。若直线 $ GE,HE $ 的斜率之积为 $ 2 $,求证:直线 $ l $ 过定点。
(1) 求曲线 $ C $ 的方程;
(2) 设 $ E(t,t)(t>0) $ 为曲线 $ C $ 上一点,不与 $ x $ 轴垂直的直线 $ l $ 与曲线 $ C $ 交于 $ G,H $ 两点(异于 $ E $ 点)。若直线 $ GE,HE $ 的斜率之积为 $ 2 $,求证:直线 $ l $ 过定点。
答案:
(1)解:连接$OM$,由题意可得$\vert OM\vert = 1$,且$M$为$NF_1$的中点,又$O$为$F_1F_2$的中点,所以$OM// NF_2$,且$\vert NF_2\vert = 2\vert OM\vert = 2$。
因为线段$F_1N$的垂直平分线与直线$F_2N$相交于点$T$,所以$\vert TN\vert=\vert TF_1\vert$,所以$\vert\vert TF_2\vert-\vert TF_1\vert\vert=\vert\vert TF_2\vert-\vert TN\vert\vert=\vert NF_2\vert = 2<\vert F_1F_2\vert = 4$。
由双曲线的定义知,动点$T$的轨迹是以$F_1,F_2$为焦点的双曲线。
设其方程为$\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1(a>0,b>0)$,则$a = 1$,$c=\frac{1}{2}\vert F_1F_2\vert = 2$,$b=\sqrt{c^{2}-a^{2}}=\sqrt{3}$。
故曲线C的方程为$x^{2}-\frac{y^{2}}{3}=1$。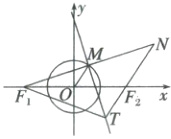
(2)证明:由
(1)知$E(1,0)$,依题意直线l的斜率存在,设直线l的方程为$y = kx + m$,$G(x_1,y_1)$,$H(x_2,y_2)$。
由$\begin{cases}y = kx + m\\x^{2}-\frac{y^{2}}{3}=1\end{cases}$,得$(3 - k^{2})x^{2}-2kmx - m^{2}-3 = 0$。
$3 - k^{2}\neq0$,由$\Delta>0$,得$m^{2}+3 - k^{2}>0$,所以$x_1 + x_2=\frac{2km}{3 - k^{2}}$,$x_1x_2=\frac{m^{2}+3}{k^{2}-3}$。
则$k_{GE}· k_{HE}=\frac{y_1}{x_1 - 1}·\frac{y_2}{x_2 - 1}=\frac{(kx_1 + m)(kx_2 + m)}{(x_1 - 1)(x_2 - 1)}=\frac{k^{2}x_1x_2+km(x_1 + x_2)+m^{2}}{x_1x_2-(x_1 + x_2)+1}=\frac{k^{2}·\frac{m^{2}+3}{k^{2}-3}+\frac{2k^{2}m^{2}}{3 - k^{2}}+m^{2}}{\frac{m^{2}+3}{3 - k^{2}}-\frac{2km}{3 - k^{2}}+1}=2$。
整理得$k^{2}-4km - 5m^{2}=0$,即$(k - 5m)(k + m)=0$,解得$k = 5m$或$k = - m$。
当$k = 5m$时,直线l的方程为$y = 5mx + m = m(5x + 1)$,直线l过定点$(-\frac{1}{5},0)$。
当$k = - m$时,直线l的方程为$y = -mx + m = m(-x + 1)$,直线l过定点$E(1,0)$,不符合题意,舍去。
综上所述,直线l过定点$(-\frac{1}{5},0)$。
(1)解:连接$OM$,由题意可得$\vert OM\vert = 1$,且$M$为$NF_1$的中点,又$O$为$F_1F_2$的中点,所以$OM// NF_2$,且$\vert NF_2\vert = 2\vert OM\vert = 2$。
因为线段$F_1N$的垂直平分线与直线$F_2N$相交于点$T$,所以$\vert TN\vert=\vert TF_1\vert$,所以$\vert\vert TF_2\vert-\vert TF_1\vert\vert=\vert\vert TF_2\vert-\vert TN\vert\vert=\vert NF_2\vert = 2<\vert F_1F_2\vert = 4$。
由双曲线的定义知,动点$T$的轨迹是以$F_1,F_2$为焦点的双曲线。
设其方程为$\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1(a>0,b>0)$,则$a = 1$,$c=\frac{1}{2}\vert F_1F_2\vert = 2$,$b=\sqrt{c^{2}-a^{2}}=\sqrt{3}$。
故曲线C的方程为$x^{2}-\frac{y^{2}}{3}=1$。

(2)证明:由
(1)知$E(1,0)$,依题意直线l的斜率存在,设直线l的方程为$y = kx + m$,$G(x_1,y_1)$,$H(x_2,y_2)$。
由$\begin{cases}y = kx + m\\x^{2}-\frac{y^{2}}{3}=1\end{cases}$,得$(3 - k^{2})x^{2}-2kmx - m^{2}-3 = 0$。
$3 - k^{2}\neq0$,由$\Delta>0$,得$m^{2}+3 - k^{2}>0$,所以$x_1 + x_2=\frac{2km}{3 - k^{2}}$,$x_1x_2=\frac{m^{2}+3}{k^{2}-3}$。
则$k_{GE}· k_{HE}=\frac{y_1}{x_1 - 1}·\frac{y_2}{x_2 - 1}=\frac{(kx_1 + m)(kx_2 + m)}{(x_1 - 1)(x_2 - 1)}=\frac{k^{2}x_1x_2+km(x_1 + x_2)+m^{2}}{x_1x_2-(x_1 + x_2)+1}=\frac{k^{2}·\frac{m^{2}+3}{k^{2}-3}+\frac{2k^{2}m^{2}}{3 - k^{2}}+m^{2}}{\frac{m^{2}+3}{3 - k^{2}}-\frac{2km}{3 - k^{2}}+1}=2$。
整理得$k^{2}-4km - 5m^{2}=0$,即$(k - 5m)(k + m)=0$,解得$k = 5m$或$k = - m$。
当$k = 5m$时,直线l的方程为$y = 5mx + m = m(5x + 1)$,直线l过定点$(-\frac{1}{5},0)$。
当$k = - m$时,直线l的方程为$y = -mx + m = m(-x + 1)$,直线l过定点$E(1,0)$,不符合题意,舍去。
综上所述,直线l过定点$(-\frac{1}{5},0)$。
【高考真题】(2023·新高考Ⅱ卷,改编)已知双曲线 $ C:\frac{x^{2}}{4}-\frac{y^{2}}{16}=1 $。记 $ C $ 的左、右顶点分别为 $ A_{1},A_{2} $,过点 $ (-4,0) $ 的直线与 $ C $ 的左支交于 $ M,N $ 两点,$ M $ 在第二象限,直线 $ MA_{1} $ 与 $ NA_{2} $ 交于点 $ P $。证明:点 $ P $ 在定直线上。
答案:
证明:由双曲线的方程可得$A_1(-2,0)$,$A_2(2,0)$,设$M(x_1,y_1)$,$N(x_2,y_2)$。
显然直线的斜率不为$0$,所以设直线$MN$的方程为$x = my - 4$,且$-\frac{1}{2}<m<\frac{1}{2}$,与$\frac{x^{2}}{4}-\frac{y^{2}}{16}=1$联立可得$(4m^{2}-1)y^{2}-32my + 48 = 0$,且$\Delta=64(4m^{2}+3)>0$。
则$y_1 + y_2=\frac{32m}{4m^{2}-1}$,$y_1y_2=\frac{48}{4m^{2}-1}$。
直线$MA_1$的方程为$y=\frac{y_1}{x_1 + 2}(x + 2)$,直线$NA_2$的方程为$y=\frac{y_2}{x_2 - 2}(x - 2)$。
故$\frac{x + 2}{x - 2}=\frac{y_2(x_1 + 2)}{y_1(x_2 - 2)}=\frac{my_1y_2-2(y_1 + y_2)+2y_1}{my_1y_2-6y_1}=\frac{m·\frac{48}{4m^{2}-1}-2·\frac{32m}{4m^{2}-1}+2y_1}{m·\frac{48}{4m^{2}-1}-6y_1}=\frac{\frac{-16m}{4m^{2}-1}+2y_1}{\frac{48m}{4m^{2}-1}-6y_1}=-\frac{1}{3}$。
由$\frac{x + 2}{x - 2}=-\frac{1}{3}$可得$x = - 1$,即$x_p = - 1$,据此可得点$P$在定直线$x = - 1$上运动。
证明:由双曲线的方程可得$A_1(-2,0)$,$A_2(2,0)$,设$M(x_1,y_1)$,$N(x_2,y_2)$。
显然直线的斜率不为$0$,所以设直线$MN$的方程为$x = my - 4$,且$-\frac{1}{2}<m<\frac{1}{2}$,与$\frac{x^{2}}{4}-\frac{y^{2}}{16}=1$联立可得$(4m^{2}-1)y^{2}-32my + 48 = 0$,且$\Delta=64(4m^{2}+3)>0$。
则$y_1 + y_2=\frac{32m}{4m^{2}-1}$,$y_1y_2=\frac{48}{4m^{2}-1}$。
直线$MA_1$的方程为$y=\frac{y_1}{x_1 + 2}(x + 2)$,直线$NA_2$的方程为$y=\frac{y_2}{x_2 - 2}(x - 2)$。
故$\frac{x + 2}{x - 2}=\frac{y_2(x_1 + 2)}{y_1(x_2 - 2)}=\frac{my_1y_2-2(y_1 + y_2)+2y_1}{my_1y_2-6y_1}=\frac{m·\frac{48}{4m^{2}-1}-2·\frac{32m}{4m^{2}-1}+2y_1}{m·\frac{48}{4m^{2}-1}-6y_1}=\frac{\frac{-16m}{4m^{2}-1}+2y_1}{\frac{48m}{4m^{2}-1}-6y_1}=-\frac{1}{3}$。
由$\frac{x + 2}{x - 2}=-\frac{1}{3}$可得$x = - 1$,即$x_p = - 1$,据此可得点$P$在定直线$x = - 1$上运动。

查看更多完整答案,请扫码查看


