《2026年学易优高考二轮总复习数学》

2.(2025·上海)2024 年巴黎奥运会，中国获得了男子 $4 × 100$米混合泳接力金牌，以下是历届奥运会男子 $4 × 100$米混合泳接力项目冠军成绩记录(单位：秒)，数据按照升序排列.
206.78 207.46 207.95 209.34 209.35
210.68 213.73 214.84 216.93 216.93
(1)求这组数据的极差与中位数；
(2)从这 10 个数据中任选 3 个，求恰有 2 个数据在 211 以上的概率；
(3)若比赛成绩 $y$ 关于年份 $x$ 的回归方程为 $\hat{y} = -0.311x + \hat{b}$，年份 $x$ 的平均数为 2006，预测 2028 年冠军队的成绩(精确到 0.01 秒).

答案： 2.解：
(1)这组数据的极差为$216.93 - 206.78 = 10.15$，
中位数为$\frac{209.35 + 210.68}{2}=210.015$．
(2)记“从这10个数据中任选3个，恰有2个数据在211以上”为事件$A$，
由题可知，这10个数据中在211以上的有4个，故$P(A)=\frac{C_{6}^{2}C_{4}^{1}}{C_{10}^{3}}=\frac{6×6}{120}×\frac{3}{10}=\frac{3}{10}$．所以所求的概率为$\frac{3}{10}$．
(3)由题可知，$\overline{x}=2006$，$\hat{y}=\frac{1}{10}×(206.78 + 207.46 + 207.95 + 209.34 + 209.35 + 210.68 + 213.73 + 214.84 + 216.93 + 216.93)=211.399$，
代入$\hat{y}=-0.311x+\hat{b}$，得$211.399=-0.311×2006+\hat{b}$，
解得$\hat{b}=835.265$，
则$\hat{y}=-0.311x + 835.265$，
将$x = 2028$代入，得$\hat{y}=204.557\approx204.56$，
故预测2028年冠军队的成绩为204.56秒．

考向 1 统计图表与数字特征的应用
例1 (1)(多选)(2025·重庆三模)从两名同学中挑出一名代表班级参加射击比赛.根据以往的成绩记录，甲、乙两名同学击中目标靶的环数 $X$(甲同学)和 $Y$(乙同学)的概率分布图分别是如图的甲、乙：通过计算，$E(X) = E(Y) = 8$，则下列说法正确的是 (BCD)


A.甲同学的平均成绩高于乙同学
B.乙同学击中 8 环的概率高于甲同学
C.甲同学击中 10 环的概率高于乙同学
D.乙同学的射击成绩更稳定

答案：
(1)BCD 由于$E(X)=E(Y)=8$，即平均水平相当，
故A错误；由图可知，甲同学击中8环的概率小于乙同学击中8环的概率，所以B正确；甲同学击中10环的概率大于乙同学击中10环的概率，所以C正确；从概率分布图来看，乙同学的成绩分布相对更集中在均值8环附近，波动更小，所以乙同学的射击成绩更稳定，故D正确，故选BCD．

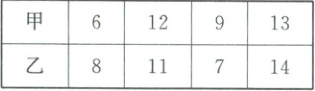
(2)(2025·新乡模拟)已知甲、乙两名篮球运动员在四场小组赛中的得分(单位：分)如下表：

则对于这两组数据，不相同的数字特征是 (B)

A.平均数
B.中位数
C.方差
D.极差

答案：
(2)B 对于A，甲的平均数为$\frac{6 + 12 + 9 + 13}{4}=10$，乙的平均数为$\frac{8 + 11 + 7 + 14}{4}=10$，故A错误；对于B，将甲从小到大排列为：6，9，12，13，所以中位数为$\frac{9 + 12}{2}=10.5$；将乙从小到大排列为：7，8，11，14，所以中位数为$\frac{8 + 11}{2}=9.5$，故B正确；对于C，甲的方差为$\frac{1}{4}[(6 - 10)^2+(9 - 10)^2+(12 - 10)^2+(13 - 10)^2]=7.5$，乙的方差为$\frac{1}{4}[(8 - 10)^2+(10)^2+(11 -学易优 高考二轮总复习 数学 10)^2+(7 - 10)^2+(14 - 10)^2]=7.5$，故C错误；对于D，甲的极差为13 - 6 = 7，乙的极差为14 - 7 = 7，故D错误．故选B．

例2 (2025·天津二模)某地组织全体中学生参加了主题为“强国之路”的知识竞赛，随机抽取了 2000 名学生进行成绩统计，发现抽取的学生的成绩都在 50 分至 100 分之间，进行适当分组后(每组的取值区间均为左闭右开区间)，画出频率分布直方图(如图)，下列说法正确的是 (C)


A.在被抽取的学生中，成绩在区间[90,100)内的学生有 750 人
B.直方图中 $x$ 的值为 0.020
C.估计全校学生成绩的中位数为 87
D.估计全校学生成绩的样本数据的 80％分位数约为 90

答案： C 由图可知，成绩在区间$[90,100)$内的频率为$0.040×10 = 0.4$，$0.4×2000 = 800$人，故A错误；由图可知，$(0.005 + 0.010 + x + 0.030 + 0.040)×10 = 1$，得$x = 0.015$，故B错误；前3组的频率和为0.3，前4组的频率和为0.6，所以中位数在第4组，所以$0.3+(x - 80)×0.03 = 0.5$，得$x\approx87$，故C正确；样本数据的80%分位数在第5组，$0.6+(x - 90)×0.04 = 0.8$，得$x = 95$，故D错误．故选C．